Representing Real Life Situations Using Exponential Functions (General Mathematics)
Summary
TLDRThe video explains exponential functions and models such as population growth, exponential decay, and compound interest. It introduces the general forms of exponential functions, explains the transformation of these functions, and covers key real-life applications. Examples include population growth during a pandemic, population tripling over time, annual interest rates, and half-life decay. The video also breaks down each problem, identifying the exponential model to be used and providing step-by-step solutions for real-world scenarios like savings growth and radioactive decay.
Takeaways
- 📈 Exponential functions have the form f(x) = b^x, where b is greater than 0, b is not equal to 1, and x is any real number.
- 🔄 Transformations of exponential functions can be represented as f(x) = a * b^(x - c) + d, where a, b, c, and d are real numbers.
- 👥 Exponential growth models population increase and can be written as y = a * b^x or y = a * (1 + r)^x, where a is the initial amount, r is the rate of growth, and b is the growth factor.
- 📉 Exponential decay is modeled as y = a * b^x or y = a * (1 - r)^x, where a is the initial amount, and r is the rate of decay.
- 💰 Compound interest follows the formula A = P * (1 + r/n)^(nt), where P is the principal, r is the interest rate, n is the number of times interest is compounded, and t is time.
- 🦠 Example: If a virus doubles every month and there are initially 5 cases, the growth function is y = 5 * 2^x.
- 👶 A population of 5800 that triples every 20 years follows the function y = 5800 * 3^(x/20).
- 📊 A town's population of 61,723 with a 1.2% annual increase is modeled as y = 61,723 * 1.012^x.
- ☢️ For exponential decay, such as a substance with a half-life of 12 days, the function is y = 50 * (1/2)^(x/12).
- 🏦 For compound interest with an initial investment of 50,000 pesos at 6% annually, the total amount after x years is A = 50,000 * 1.06^x.
Q & A
What is the general form of an exponential function with base b?
-The general form of an exponential function with base b is f(x) = b^x, where b > 0 and b ≠ 1, and x is any real number.
How is the transformation of an exponential function represented?
-The transformation of an exponential function with base b is represented as f(x) = a * b^(x - c) + d, where a, c, and d are real numbers, and b > 0 and b ≠ 1.
What is the exponential growth model for population?
-The exponential growth model for population is y = a * b^x or y = a * (1 + r)^x, where y is the population after time x, a is the initial amount, b is the growth factor (1 + r), and r is the growth rate as a decimal.
What is the formula for exponential decay?
-The formula for exponential decay is y = a * b^x or y = a * (1 - r)^x, where y is the remaining population after time x, a is the initial amount, b is the decay factor (1 - r), and r is the rate of decay as a decimal.
How is compound interest calculated in exponential models?
-Compound interest is calculated using the formula A = P * (1 + r/n)^(nt), where A is the compound amount, P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the time in years.
What are the steps to represent real-life situations using exponential functions?
-The steps are: 1) Identify the type of scenario (e.g., population growth, decay, compound interest). 2) Determine the appropriate exponential model. 3) Identify the given values. 4) Write the function or number sentence representing the situation.
How do you model a population that doubles every month?
-The model for a population that doubles every month is y = a * 2^x, where a is the initial population and x is the number of months.
How is exponential growth represented when a population triples every 20 years?
-For a population that triples every 20 years, the model is y = a * 3^(x/20), where a is the initial population and x is the number of years.
How do you model population growth with a given annual percentage increase?
-The model for population growth with an annual percentage increase is y = a * (1 + r)^x, where a is the initial population, r is the annual growth rate as a decimal, and x is the number of years.
How do you model the decay of a substance with a known half-life?
-The decay of a substance with a known half-life is modeled by y = a * (1/2)^(x/h), where a is the initial amount, x is the elapsed time, and h is the half-life of the substance.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

REPRESENTING REAL-LIFE SITUATIONS USING EXPONENTIAL FUNCTIONS || GRADE 11 GENERAL MATHEMATICS Q1

Fungsi Eksponensial Matematika Lanjut Kelas XI

Fungsi Eksponen Pertumbuhan dan Peluruhan
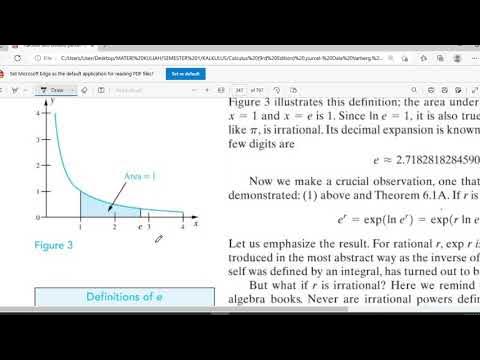
Fungsi Transenden 3 (Fungsi Eksponensial Natural)

Fungsi Eksponen Matematika Peminatan Kelas X - Apersepsi Masalah COVID-19

Fungsi Eksponen Kelompok 4
5.0 / 5 (0 votes)
