REPRESENTING REAL-LIFE SITUATIONS USING EXPONENTIAL FUNCTIONS || GRADE 11 GENERAL MATHEMATICS Q1

Summary

This educational video explores the concept of exponential functions, demonstrating their form and applications in real-life scenarios. It covers the definition of exponential functions, examples with bases greater than zero and not equal to one, and their use in modeling population growth, exponential decay, and compound interest. The script also explains how to construct a table of values for exponential functions and provides step-by-step calculations for various examples, including bacteria growth, radioactive decay, and investment growth. The video concludes with an introduction to the natural exponential function with base e, illustrating its application in temperature change.

Takeaways

• 📚 Exponential functions are mathematical functions of the form \( f(x) = b^x \) where \( b > 0 \) and \( b \neq 1 \).
• 🚫 The base of an exponential function cannot be one because it would result in a constant function regardless of the exponent.
• 📈 Examples of exponential functions include \( f(x) = 6^x \), \( f(x) = 16^x \), and \( f(x) = 3^x + 1 \).
• 🔢 For exponential functions with negative bases, such as \( -4 \) raised to \( 1/2 \), the result is the square root of the base's reciprocal.
• 📊 A table of values for different functions like \( y = (1/3)^x \), \( y = 10^x \), and \( y = 0.8^x \) can be constructed by substituting various values of \( x \).
• 🌱 Applications of exponential functions include modeling population growth, where quantities can double or triple over certain time periods.
• 📉 Exponential decay, such as the half-life of radioactive substances, can also be modeled using exponential functions.
• 💰 Compound interest is another real-life application where the amount of money grows exponentially over time.
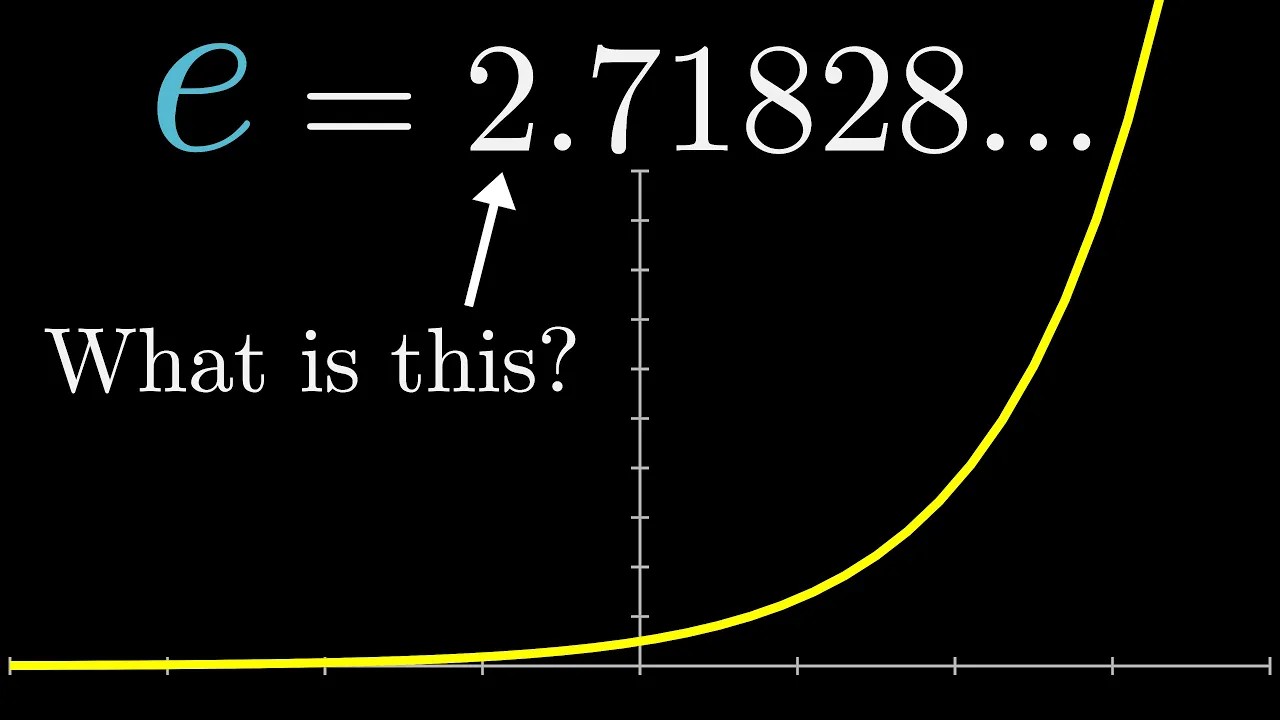
• 🔢 The natural exponential function uses the base \( e \) (approximately 2.71828), which is a fundamental constant in mathematics.
• 📉 A table of values for a function involving the natural base \( e \), like the temperature of a meat slab in an oven, can show how the temperature changes over time.
• 🛠️ Using a scientific calculator is recommended to evaluate and check the results of exponential functions and their applications.

Q & A

What is an exponential function?

An exponential function is a mathematical function of the form f(x) = b^x, where b is the base and x is the exponent. The base b must be greater than 0 and not equal to 1.

Why can't the base of an exponential function be 1?

If the base b is equal to 1, then for any value of x, the function will always yield a result of 1, making it a constant function rather than an exponential one.

What are some examples of exponential functions mentioned in the script?

Examples include f(x) = 6^x, f(x) = 16^x, and f(x) = (3^x) + 1.

Why is the function f(x) = x^3 not considered an exponential function?

The function f(x) = x^3 is not an exponential function because the base is x, which is a variable, and not a constant greater than 0 and not equal to 1.

How do you construct a table of values for an exponential function?

You substitute given values of x into the function and calculate the corresponding y values. This process is repeated for each x value to create the table.

What is the significance of the base being greater than zero in an exponential function?

The base being greater than zero ensures that the function will yield positive values for any real number x, which is a requirement for an exponential function.

What is the formula for an exponential growth model in terms of population?

The formula for an exponential growth model is y = y0 * (growth rate)^(t/time period), where y0 is the initial population, t is the time elapsed, and the growth rate is typically a factor greater than 1.

How is the concept of half-life used in exponential decay?

In exponential decay, the half-life is the time it takes for half of the substance to decay. The remaining amount of substance after time t is given by y = y0 * (1/2)^(t/half-life period).

What is the formula for compound interest using an exponential function?

The formula for compound interest is A = P * (1 + r)^t, where A is the amount of money accumulated after n years, including interest, P is the principal amount, r is the annual interest rate, and t is the time the money is invested for in years.

What is the natural base e used for in exponential functions?

The natural base e, approximately equal to 2.71828, is a fundamental mathematical constant used as the base for the natural exponential function. It is commonly used in calculus and various scientific fields.

Outlines

00:00

📚 Introduction to Exponential Functions

This paragraph introduces the concept of exponential functions, defining them as functions of the form f(x) = b^x, where b is greater than zero and not equal to one. It explains that the base b cannot be one, as it would make the function a constant. Examples of exponential functions are given, such as f(x) = 6^x, f(x) = 16^x, and f(x) = (3 + 1)^x. The paragraph also clarifies that f(x) = x^x is not an exponential function because the base is variable. It concludes with an instruction to complete a table of values for various x values using the given function y = (1/3)^x.

05:00

🔢 Evaluating Exponential Functions and Their Applications

The second paragraph delves into the evaluation of exponential functions with different bases, including 1/3, 10, and 0.8, for a range of x values. It demonstrates the process of substituting values into the functions to find corresponding y values, emphasizing the use of reciprocals for negative exponents. The paragraph also discusses the application of exponential functions in real-life scenarios such as population growth, exponential decay, and compound interest, providing a basic formula for population growth based on doubling time.

10:03

🌿 Exponential Growth in Bacterial Population

This paragraph focuses on the application of exponential functions to model the growth of bacterial populations. It uses an example where bacteria double every 100 hours, starting with an initial count of 20. The paragraph constructs an exponential model to represent the number of bacteria over time, y = 20 * 2^(t/100), and demonstrates how to calculate the number of bacteria at various time intervals, such as 100, 200, 300, and 400 hours.

15:05

⏳ Modeling Half-Life Decay with Exponential Functions

The fourth paragraph discusses the use of exponential functions to model the decay of radioactive substances over time, known as half-life decay. It provides a formula for calculating the remaining amount of a substance after a given time, y = y0 * (1/2)^(t/t_half), where y0 is the initial amount, t_half is the half-life, and t is the time elapsed. Examples are given to illustrate how to determine the remaining quantity of a substance after specific time periods, such as 30 days for a substance with a 10-day half-life and 600 years for one with a 400-year half-life.

20:07

🏦 Compound Interest and Natural Exponential Functions

The final paragraph explores the concept of compound interest, which is calculated using an exponential function. It explains how to calculate the future value of an investment using the formula A = P * (1 + r)^t, where P is the principal amount, r is the annual interest rate, and t is the time in years. An example is provided where an investment of 100,000 earns 6% interest compounded annually, with the future value calculated for five years. The paragraph also introduces the natural exponential function with base e, an irrational number approximately equal to 2.71828, and provides an example of how it can be used to model the heating of a meat slab in an oven.

Keywords

💡Exponential Function

An exponential function is a mathematical function of the form f(x) = b^x, where 'b' is the base and 'x' is the exponent. In the video, it is defined as a function where the base 'b' is greater than zero and not equal to one. This function is central to the video's theme, illustrating various real-life applications such as population growth and decay processes. For example, the script mentions 'f(x) = 6^x' as an example of an exponential function.

💡Base

In the context of exponential functions, the base is the number which is raised to the power of the variable. The script specifies that the base must be greater than zero and not equal to one to be considered an exponential function. The base is crucial as it determines the rate at which the function grows or decays, as seen in functions like 'f(x) = 16^x' discussed in the video.

💡Half-Life Decay

Half-life decay refers to the time it takes for half of the substance to decay. This concept is used in the video to demonstrate how exponential functions can model the decay of radioactive substances over time. The script provides an example where the half-life is 10 days, and it shows how the amount of a substance decays to 1.25 grams after 30 days using an exponential model.

💡Compound Interest

Compound interest is the interest on a loan or investment that is added to the principal amount, and then contributes to the interest in the next period. The video explains how exponential functions can model compound interest, showing how investment grows over time with interest added to the initial amount. An example given is Mrs. Dilacross investing 100,000 with an annual interest rate of 6% compounded annually.

💡Population Growth

Population growth is a concept used in the video to illustrate the application of exponential functions in modeling how a quantity, such as bacteria, grows over time. The script describes a scenario where bacteria double every 100 hours, and an exponential model is used to predict the number of bacteria after a certain period.

💡Table of Values

A table of values is a method to organize and display the output of a function for different input values. In the video, constructing a table of values for various functions like 'y = (1/3)^x' and 'y = 10^x' helps visualize the behavior of exponential functions for different 'x' values. The script uses this method to demonstrate how the output changes with different inputs.

💡Natural Exponential Function

The natural exponential function uses the base 'e', an irrational number approximately equal to 2.71828. The video distinguishes this function as a special case of exponential functions, often used in calculus and natural processes. An example provided in the script uses 'e' to model the temperature increase of a meat slab in an oven.

💡Reciprocal

The reciprocal of a number is the value which, when multiplied by the original number, results in one. In the context of the video, when dealing with negative exponents in exponential functions, the reciprocal is used. For instance, '3^(-2)' is the reciprocal of '3^2', and the script explains this concept when discussing the function 'y = 3^x'.

💡Interest Rate

The interest rate is the percentage at which an investment will grow or a loan will accumulate interest over a year. In the video, the interest rate is a key component in the exponential model for compound interest. It is used to calculate the future value of an investment, as shown with the 6% annual interest rate in the investment example.

💡Principal

The principal is the initial amount of money invested or borrowed, on which interest is calculated. In the video, the principal amount is essential in the exponential model for compound interest, as it is the base amount that will grow over time. The script uses a principal of 100,000 in the investment growth example.

💡Exponential Decay

Exponential decay is the process by which a quantity decreases at a rate proportional to its current value. The video script discusses this concept in the context of half-life decay, showing how the amount of a substance reduces exponentially over time. An example of this is the radioactive substance with a half-life of 10 days decaying to 1.25 grams after 30 days.

Highlights

Introduction to exponential functions with the form f(x) = b^x, where b > 0 and b ≠ 1.

Explanation of why b cannot equal 1 in an exponential function.

Examples of exponential functions with different bases.

Clarification that f(x) = x^3 is not an exponential function due to the variable base.

Demonstration of how to evaluate exponential functions with negative bases and exponents.

Instruction on constructing a table of values for exponential functions.

Example calculations for y = (1/3)^x with various x values.

Explanation of the exponential growth model in the context of population growth.

Real-life example of bacteria doubling in number every 100 hours.

How to calculate the number of bacteria after a certain time using an exponential model.

Application of exponential functions to model half-life decay.

Example of calculating remaining radioactive substance after a given time.

Introduction to compound interest as an application of exponential functions.

Explanation of how to calculate the future value of an investment with compound interest.

Use of the natural exponential function with base e in modeling real-life scenarios.

Example of modeling the heating of a meat slab in an oven using an exponential function.

Construction of a table of values to interpret the temperature increase of the meat slab over time.

Encouragement to use scientific calculators for evaluating exponential functions.

Closing remarks with a call to like, subscribe, and follow for more educational content.

Transcripts

[Music]

in this video we are going to

represent real life situation using

exponential

function an exponential function with

base b

is a function of the form f of x is

equal to b

raised to x or y is equal to b raised to

x

where b is greater than zero and b

should not be

equal to one so bucket indicative again

equals to one

because say once we sub uh once the base

is

one and any value of x like substituting

your

x still the answer is one so mugging

constant name function not nothing

initial exponential function

making constant

okay examples of exponential function

we have f of x is equal to 6 raised to

x f of x is equal to 16

raised to x and f of x is equal to 3

raised to x

plus 1 so so unan example in base

nothing that is six

and this is exponential function bucket

um base net in a

greater than zero and then hindi equals

one and so pangala wang function at n

the base is 16

sapangatung function at n the base is

three

itunes in the exponential

function so f of x is equal to x cube

bucket indica

exponential function because uh

jung base nothing is variable so

hinduisha exponential function

f of x is equal to 1 raised to x

so since you base not n is one

therefore hindusha exponential function

f of x is equal to x raised to x this is

also not

exponential function bucket in base

nation

negative numbers you base not n for

example melon tile

it based the negative four and your

exponent nothing is one half

we try to evaluate this so

negative four raised to one half kappa

and evaluate nothing negative four

raised to one half the answer is square

root of

negative four at independent negative

first

inside of radicand

hindi long uh hindi padding one and

game base mo greater than zero but not

equal to one

okay complete a table of values for x is

equal to negative three

negative two negative one zero one two

and three okay we have a given function

here

and then we substitute the given values

and

so i try to have a to construct a table

of values

using the given values of x okay

so we have negative three negative two

negative one zero one two

and three now okay we have first

function y

y is equal to one third raised to x this

is

exponential why because one third is

greater than zero attuned based not in a

ind equals one

so therefore y is equal to one third is

raised to x

and this is exponential function so on

gaga indiana

and substitute magnet is negative 3 in

our x so

exponent not in a negative numbers so

gagawing lang reciproc

so 3 raised to 3 that is 27 so same

process

negative 2 so since an exponent not in a

negative

so level reciprocal and then that will

become

three squared and the answer is nine

so three raised to negative uh one third

raised to negative one get the

reciprocal and three raised to one that

is

uh one so nothing reciprocal

exponent next one third raised to zero

that

is one so any number raised to zero the

answer is one

one third raised to one that is one

third

one third raised to two that is

one over nine because one times one that

is one

three times three that is nine and one

third

raised to three that is one over twenty

seven

so the second function that we have is y

is equal to ten raised to x

so y is equal to ten raised to x so

substituting nothing in my

negative three so that is one over one

thousand bucket

since negative your exponent nothing you

will coordinating your reciprocal that

will become one over ten

raised to negative at 10 raised to 3

since uh reciprocal so that will become

1

raised to 10 uh 1 over 10 raised to 3.

energy 1 over

1 000 same process negative to it that

will become 1 over 100

okay negative 1 that is 1 over 10 so 10

raised to the zeros

that answer is 1 10 raised to 1 10

10 raised to 2 or 10 squared is 100

10 cube is 1000 and the last function

that we have

is y is equal to 0.8 raised to x

so 0.8 is greater than zero

zero and not equal to one so therefore y

is equal to 0.8 raised to

x is x it's an exponential function so

substitute like nothing you might given

values than x

so apache enough to cheat nothing you

can use your scientific calculator

to check the answer so 0.8 raised to

negative to the answer is 1.5625

and then 0.8 raised to negative 1. so

since negative young it raises a program

so the answer is one point

twenty-five zero point eight raised to

zero the answer is one

and zero point eight raised to one that

is zero point eight zero point eight

raised to two that is zero point sixty

four

zero point eight raised to three that is

zero 0.512

so you can check this using your

calculator

later my uh gagamite calculator to

evaluate and to check our answer so the

pata pusing in video

calculator

for example number two we have f of x is

equal to three raised to

x evaluate f of two f of negative two

f of one half and f of zero point four

some gagavindang nathan papa little x

nathan

nama given values netanyahu negative to

one half 0.4

so if our x is two so f of two that will

become three squared

so three squared that is equal to nine

so f of negative two so again three

raised to negative two since negative

your exponent not

n get the reciprocal so that will become

one over three squared

and one over three squared that is one

over nine

next f of one half three raised to one

hops up again eval

and evaluate that into it will become

square root of three another we have

f of zero point four so that will become

three raised to zero point four

is equal to three raised to two over

five y two over five

kappa key convert not into zero point

first decimal so that will become four

over ten

so get the lowest term of four over ten

that is two over five

and then and evaluate nothing and three

raised to two over five that will become

fifth root of three squared and

threes this it will become fifth of

nine

okay the most common application in real

life of exponential function

and their transformation are population

growth

exponential decay and compound interest

so

if you uh real life application

ex exponential function so it says

exponential models and population growth

suppose a quantity y

doubles every t units of time if y sub

zero is the initial amount

then the quantity y after t units of

time is given by

y is equal to y sub zero times two by

two so young to d

is not a dependence given since double c

and so

out to yan that and then nothing y sub

zero that is the initial

amount raised to t over t so you capital

letter t that is the units of time

for example let t is equal to time in

days

at t is equal to zero there were

initially 20 bacteria

suppose that the bacteria double every

100 hours

give an exponential model for the

bacteria as a function of

t initially it is equal to zero so the

number of bacteria is 20

at the start so you number them bacteria

is 20 and then

magda double the double shot in every

hundred hours

so pagnetting the 100 are sodium

bacteria and the number of bacteria is

40 because 20 times to that is 40.

so pack that thing in 200 rs the

doubling of the monument 49 and somebody

getting 18 ah

so 2 squared that is 4 times 2 that is

80.

after 300 r are the doubling the

eighteen ion

that will become one sixty so upon uh

synonym to find that two raised to three

that is eight

times twenty that is one sixty and then

after 400

rs this is now uh 116 canadians

on the dome that is 320 now after 400

hours so t uh 400 hours 2 raised to 4

16 times 20 that is 320

or in this situation we can represent

using the exponential model

y is equal to 20 times 2 raised to t

over 100 so again sana kuwaiyan 20

that is the initial number of bacteria

italian

and then you do not want nothing because

the given is double

and the new one hundred nakhon and this

is the unit of time so

unit of time nothing detail is 100

hours so if we can check

nope neck nothing let's say check

nothing you 100 so 100 divide 100 so

that is 1.

2 raised to 1 is 2 times 20 that's still

40.

okay so this is not exponential model

for this situation

i'll give you another okay for another

example

at time t is equal to zero 500 bacteria

are in petri dish and this amount

triples every 15 days so we're going to

answer these

q questions given exponential models for

the situation

how many bacteria in the dish after 40

days

so using the exponential model kanina so

we're going to identify

the following so under your y subscribe

zero that is the initial amount or the

initial number

so i know by initial amount mapping jan

so that is 500 so therefore y

sub zero papadi 500

next you capital letter t that

is the unit of time so 11 units of time

not in jan

so that is 15 days so therefore that is

15. so papayta not into num15

so we can represent our exponential

model in this situation by

y is equal to 500 times 3 bucket 3

because of the word triples okay

raised to t over 15. so we can answer

now

the letter b question how many bacteria

in the dish after 40 days so

after 40 days so what we're going to do

is simply substitute

on the exponential models that we have

so 500 times 3 raised to 40 over 50

that is 9360

so that is equivalent for 900 9360

why uh we're going to

uh round up our answer into whole number

because

nothing is number of bacteria therefore

there will be 9 360 bacteria after 40

days

or using your scientific calculator you

can use

uh your scientific calculator to

using your calculator so

data 500 open parenthesis that is three

closed double spin the cube exponent

and then production var that is

so we can check our uh

answer kuntama okay the answer is nine

thousand

three hundred sixty okay thank you

sakasha then the download view

emulator

so another application of uh exponential

function is the half-life decay

so the half-life decay of a radioactive

substance it takes for half

of the substance to decay exponential

function and half-life if the half-life

of a substance is

t units and y sub zero

is the amount of the substance

corresponding to t

is equal to zero then the amount y of

substance remaining after t

units of time is given by y is equal to

y sub zero

times one half raised to t over

t or the unit of time so as you can see

palance

uh example nothing that's a population

growth

because of the half life okay for

example

suppose that the half-life of a certain

radioactive substance

is 10 days and there are 10 grams

initially

determine the amount of substance

remaining after

30 days okay so let's have first a

representation

in a certain time no so

at the start the amount of substance is

10 grams

so maga half life sha no naga hapsha

after uh 10 days every 10 days so

so in 10 days so 5 grams

so after 20 days so five grams yes

so that will become 2.5 grams and after

30 days so mahatma lit and that will

become 1.25 grams

so therefore the amount of substance

remaining after 30 days

is 1.25 grams so in this situation

we can represent using exponential model

by y is equal to 10

again 10 that is the initial amount or

initial number

times one-half one-half because of

half-life

raised to t over 10 and 10 is the

unit of time that is the 10 days now

from the given so another example the

half-life of a substance

is 400 years give an exponential model

for the situation

how much will remain after 600 years

if the initial amount was 200 grams

so on the initial amount not in detail

200 grams and then

what is the unit of time 400 years so

400 years in unit of time not in chin

so using this exponential model so y is

equal to 200

times one half raised to t over 400

so again 200 that is the initial amount

one half because of half-life

400 because that is the unit of time 400

years

so nothing young remaining

uh number of

substance so after 600 years

so t is equal to 600 sub digit log

naught is exponential model nut

and a y is equal to 200 times one half

raised to t over 400 and that will

become

y is equal to 200 times one one-half

raised to 600

over 400 that's that is equivalent to

70.71 grams okay

you can use your calculator okay

so again pretty nothing committing only

your calculator nothing

so that is opinion at 10

so we have 200

then open parenthesis of fraction lagena

1

and then down arrow that is 2

then close parenthesis

and then it open exponent that and so

like a dino production bar

and that is 600

okay down that is 400

so equal so that is 70.71

grams okay

another application of exponential

models

is no exponential function rather is

the compound interest a starting amount

of money called a principal can be

invested at a certain

interest rate that is earned at the end

of a given period of time

such as one year if the interest rate is

compounded

the interest earned at the end of the

period is added

the principal and this new amount will

earn

interest in the next period of time

the same process is repeated for each

succeeding period interest previously

earned

will also earn interest in the next

period

so by using this so using this um

exponential model we have p as the

principal

amount and r is the annual rate

and t is the uh time the amount after

time years is given so we can use this

exponential model for

compound interest for example

mrs dilacross invested 100 000

in a company that offers six percent

interest compounded annually

how much will this investment be worth

at the end of each year

for the next five years so using the

exponential model

a is equal to p times one plus r

raised to t so any principal amount not

in gen that is one hundred thousand

and the annual rate is six percent so

percent need we need to convert into

decimal

and our time the given time is five

years

so what you can do is substitute all the

given values in the

uh a is equal to p times one plus r

raised to t

so you can use that uh exponential model

so

we get uh this is equivalent to 132

822 pesos and 56 centavo

so you can use again your calculator to

check

okay so we can use the calculator to

check

that is 100 100

000. times

one point zero six

close parenthesis and then

up into tenulanto and then the game five

and then equals so 133

822.56 so we need to round off into two

decimal places now okay next

while an exponential function may have

voice bases

okay base says a frequently used base is

the irrational number

e whose value is approximately two point

seven one

eight two eight so in the internet tower

nothing natural exponential function

capacity base nut and i e

or that is approximately two point seven

one eight two eight

so calculator in your so

ito and then equals so

that is 2.71828

okay so that's the value of the natural

number or the

letter e not n i'll give you an example

a large slob of meat is taken from the

refrigerator and placed in a preheat

heated oven the temperature t of the

slab t

minutes after being placed in the oven

is given by t

is equal to 170 minus 165

e raised to negative 0.06 t

degrees celsius construct a table of

values

for the following value of t 0 10

20 30 40 50 60 and

interpret your results round off values

to the nearest integer

so by using this t is equal to 170

minus 165 e raised to negative zero

point zero zero six

t so we can substitute the value of d

zero ten twenty thirty forty fifty and

sixty so you can use your calculator

okay to check that answer so and sabi

dito

interpret your results so round off your

values to the near side so what will be

our interpretation based on the result

data so the slope of meat is increasing

in temperature at roughly the same

rate okay the somalian scientific

calculator

in scientific calculators

downloads the app store

is a cellphone so you can download this

called business

thank you for watching this video i hope

you learned something

don't forget to like subscribe and hit

the bell button

put updated ko for more video tutorial

this is your guide in learning your mod

lesson your walmart

channel