AP Precalculus – 1.6 End Behavior and Polynomial Functions
Summary
TLDRThis educational video script focuses on polynomial functions and their end behavior. It explains how polynomials either rise or fall indefinitely and introduces the concept of limits as x approaches positive or negative infinity. The script uses examples and notation to demonstrate how the degree and leading coefficient of a polynomial determine its end behavior, with even degrees leading to the same behavior on both sides and odd degrees causing opposite behaviors. The instructor emphasizes the importance of identifying the leading term to predict the function's long-term trends without needing the entire equation or graph.
Takeaways
- 📚 Polynomial functions never go constant; they either increase or decrease.
- 🔍 End behavior focuses on the behavior of a function as it approaches very large or very small values.
- 📉 For polynomial functions, as x goes to negative infinity, the function will either go down or up depending on its characteristics.
- 📈 As x goes to positive infinity, the function's behavior is also determined by its characteristics and will either increase or decrease.
- 🔢 The notation for describing the left-hand side behavior is lim(x -> -∞), and for the right-hand side, it's lim(x -> ∞).
- 📋 The end behavior can be described using mathematical notation, such as lim(x -> -∞) P(x) = ±∞ and lim(x -> ∞) P(x) = ±∞.
- 🔑 The leading term of a polynomial function, which has the highest degree, dictates the end behavior of the function.
- 🔄 For even-degree polynomials, the end behavior on the left and right is the same, influenced by the sign of the leading coefficient.
- 🔄 For odd-degree polynomials, the end behavior on the left and right is opposite, with the direction influenced by the sign of the leading coefficient.
- 📈 The end behavior can be easily determined by examining the leading term without needing the entire polynomial equation or its graph.
Q & A
What is end behavior in polynomial functions?
-End behavior in polynomial functions refers to the behavior of the function as the input (x-value) approaches either positive or negative infinity. It describes whether the function values increase or decrease without bound as x moves very far to the left or right.
How does a polynomial function behave as it approaches negative infinity?
-The behavior of a polynomial function as it approaches negative infinity depends on the leading term of the polynomial. If the leading term has an odd degree, the function will go to negative infinity on the left. If the degree is even, the function will go in the same direction as the leading coefficient (up if positive, down if negative).
What is the mathematical notation used to describe the behavior of a function as x approaches negative infinity?
-The mathematical notation used to describe the behavior of a function as x approaches negative infinity is 'lim (x→-∞) f(x)'. This notation helps to express the end behavior on the left-hand side of the function.
How can you determine the end behavior of a polynomial function without looking at its graph?
-You can determine the end behavior of a polynomial function without looking at its graph by examining the leading term of the polynomial. The sign and degree of the leading coefficient will indicate whether the function goes to positive or negative infinity on the left or right.
What is the significance of the degree of the leading term in determining the end behavior of a polynomial function?
-The degree of the leading term in a polynomial function is significant because it determines whether the end behaviors on the left and right are the same (even degree) or opposite (odd degree). An even degree polynomial will have the same end behavior on both sides, while an odd degree polynomial will have opposite end behaviors.
If the leading coefficient of a polynomial function is positive and the degree is even, what is the end behavior as x approaches negative infinity?
-If the leading coefficient is positive and the degree is even, the end behavior as x approaches negative infinity is that the function values will go to negative infinity. This is because the positive leading coefficient will cause the function to curve downwards as x becomes very large and negative.
Can you provide an example of a polynomial function with odd degree and describe its end behavior?
-An example of a polynomial function with an odd degree is f(x) = x^3. The end behavior of this function is that as x approaches negative infinity, the function goes to negative infinity, and as x approaches positive infinity, the function goes to positive infinity, demonstrating opposite end behaviors.
What does it mean if the end behaviors on the left and right sides of a polynomial function are the same?
-If the end behaviors on the left and right sides of a polynomial function are the same, it means that the function either goes to positive infinity on both sides (if the leading coefficient is positive) or goes to negative infinity on both sides (if the leading coefficient is negative). This occurs when the leading term of the polynomial has an even degree.
How do you describe the end behavior of a polynomial function mathematically when the leading term has an odd degree and a negative leading coefficient?
-When the leading term has an odd degree and a negative leading coefficient, the end behavior is described mathematically as 'lim (x→-∞) f(x) = +∞' and 'lim (x→+∞) f(x) = -∞'. This indicates that the function values increase without bound as x approaches negative infinity and decrease without bound as x approaches positive infinity.
What is the practical application of understanding end behavior in polynomial functions?
-Understanding end behavior in polynomial functions is crucial in various fields such as physics, engineering, and economics, where it helps in predicting long-term trends or behaviors of systems modeled by polynomial equations.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Grade 10 - Illustrating and graphing polynomial functions | SirABC
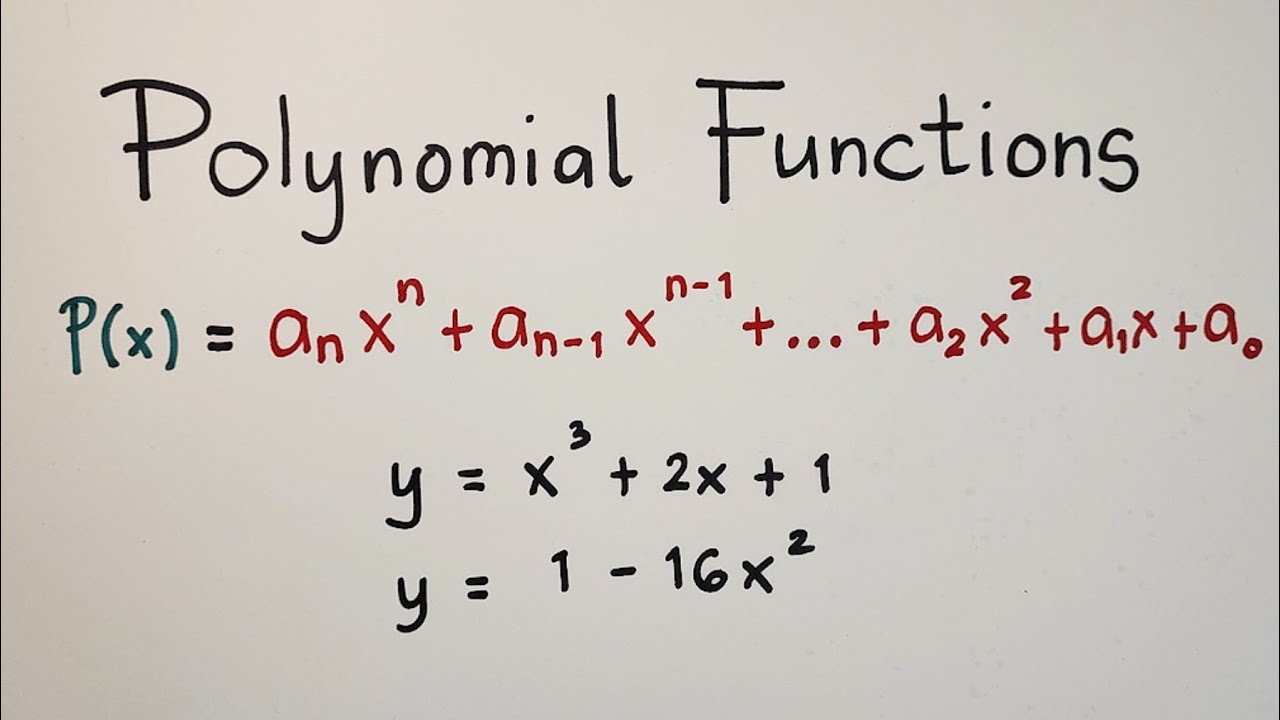
Polynomial Functions - Polynomial Function or NOT? Grade 10 Math Second Quarter
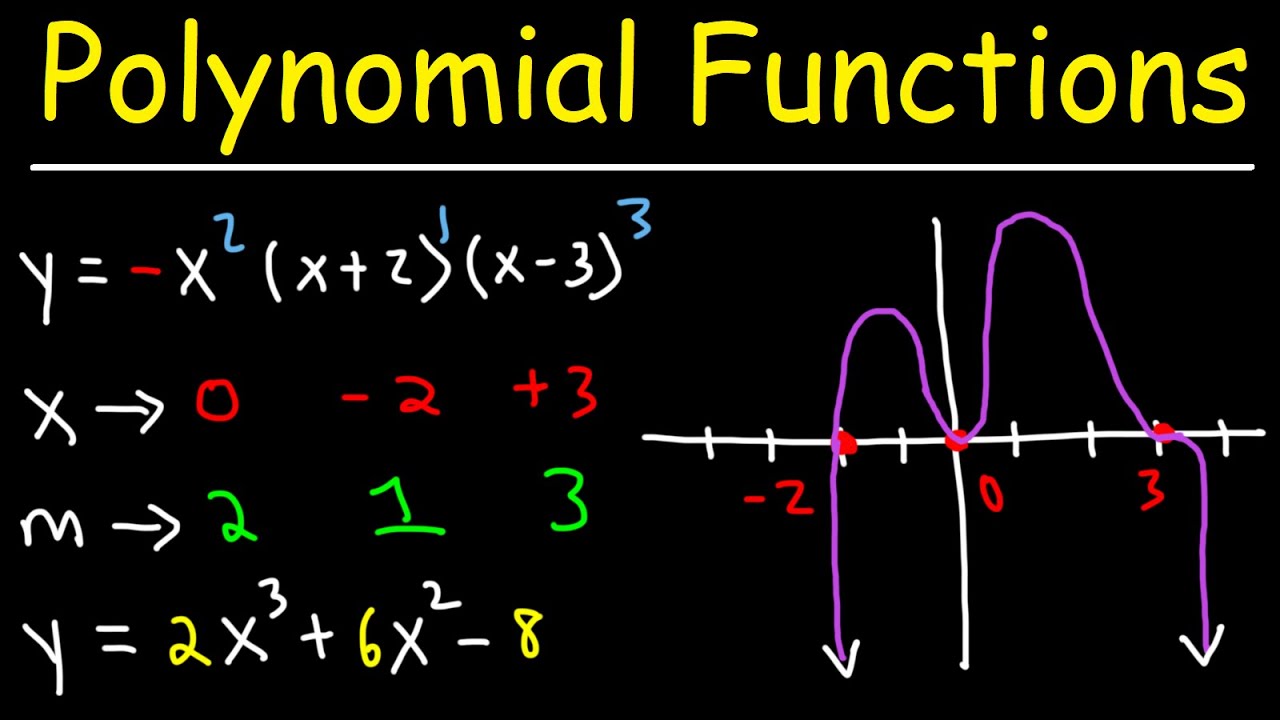
How To Graph Polynomial Functions Using End Behavior, Multiplicity & Zeros

Polinomial (Bagian 5) - Cara Menentukan Akar-akar Persamaan Polinomial

Synthetic Division of Polynomials

Lec 46 - Exponential Functions: Graphing
5.0 / 5 (0 votes)
