INTERSECCIONES DE UNA GRÁFICA CON LOS EJES X e Y 📈
Summary
TLDREn este vídeo se explica cómo encontrar las intersecciones de la gráfica de la función y = x^3 - 4x con los ejes X e Y. Al igualar y a 0, se resuelve la ecuación para encontrar los puntos en el eje X, obteniendo x = -2, x = 2 y x = 0. Al igualar x a 0, se determina que la intersección con el eje Y es en el punto (0, 0). Se describen los pasos de factorización y se visualiza el bosquejo de la gráfica con los puntos de intersección.
Takeaways
- 📉 En el video se busca determinar las intersecciones de la gráfica de la función y = x^3 - 4x con los ejes X e Y.
- 🔄 Para encontrar las intersecciones con el eje X, se iguala y a 0, lo que da la ecuación x^3 - 4x = 0.
- 🧮 El siguiente paso es factorizar x^3 - 4x, encontrando que se puede factorizar como x(x^2 - 4) = 0.
- ✂️ Luego, se aplica la diferencia de cuadrados a x^2 - 4, lo que resulta en x(x - 2)(x + 2) = 0.
- 🔢 Los factores se igualan a 0, generando tres soluciones para x: x = -2, x = 2 y x = 0.
- 📍 Esto indica que las intersecciones con el eje X son en los puntos (-2, 0), (2, 0) y (0, 0).
- ✖️ Para encontrar la intersección con el eje Y, se iguala x a 0 en la ecuación original.
- ⚖️ Al hacer x = 0, se concluye que y = 0, lo que genera una única intersección en el origen (0, 0).
- 🗺️ Se hace un bosquejo de la gráfica, mostrando los puntos de intersección con los ejes X e Y.
- 📊 El video muestra un método sistemático para hallar intersecciones mediante factorización y análisis de la función.
Q & A
¿Qué objetivo tiene el vídeo?
-El objetivo del vídeo es determinar las intersecciones que tiene una gráfica con los ejes X e Y, específicamente para la función y = x^3 - 4x.
¿Cómo se encuentran las intersecciones con el eje X?
-Para encontrar las intersecciones con el eje X, se iguala y a 0 y se resuelve la ecuación x^3 - 4x = 0.
¿Cuál es el primer paso al factorizar la ecuación x^3 - 4x = 0?
-El primer paso es observar que x es un factor común en todos los términos, por lo que se factoriza como x(x^2 - 4).
¿Cómo se aplica la diferencia de cuadrados en la ecuación?
-La diferencia de cuadrados se aplica en el término x^2 - 4, que se factoriza como (x - 2)(x + 2).
¿Cuáles son los factores que resultan de la factorización completa de la ecuación?
-Los factores resultantes son x, (x - 2) y (x + 2).
¿Qué valores de x se obtienen al igualar cada factor a 0?
-Al igualar cada factor a 0, se obtienen los valores x = 0, x = 2 y x = -2.
¿Cuáles son las intersecciones con el eje X para la función dada?
-Las intersecciones con el eje X son (-2, 0), (2, 0) y (0, 0).
¿Cómo se encuentran las intersecciones con el eje Y?
-Para encontrar las intersecciones con el eje Y, se iguala x a 0 y se resuelve la ecuación y = 0.
¿Cuál es el resultado de la ecuación y = x^3 - 4x cuando x = 0?
-Cuando x = 0, la ecuación se simplifica a y = 0^3 - 4*0, lo que resulta en y = 0.
¿Cuál es la intersección con el eje Y para la función dada?
-La intersección con el eje Y es (0, 0).
¿Cómo se representa gráficamente la función y = x^3 - 4x con sus intersecciones?
-La función se representa gráficamente con los puntos de intersección (-2, 0), (2, 0) y (0, 0), y una curva que pasa por estos puntos.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
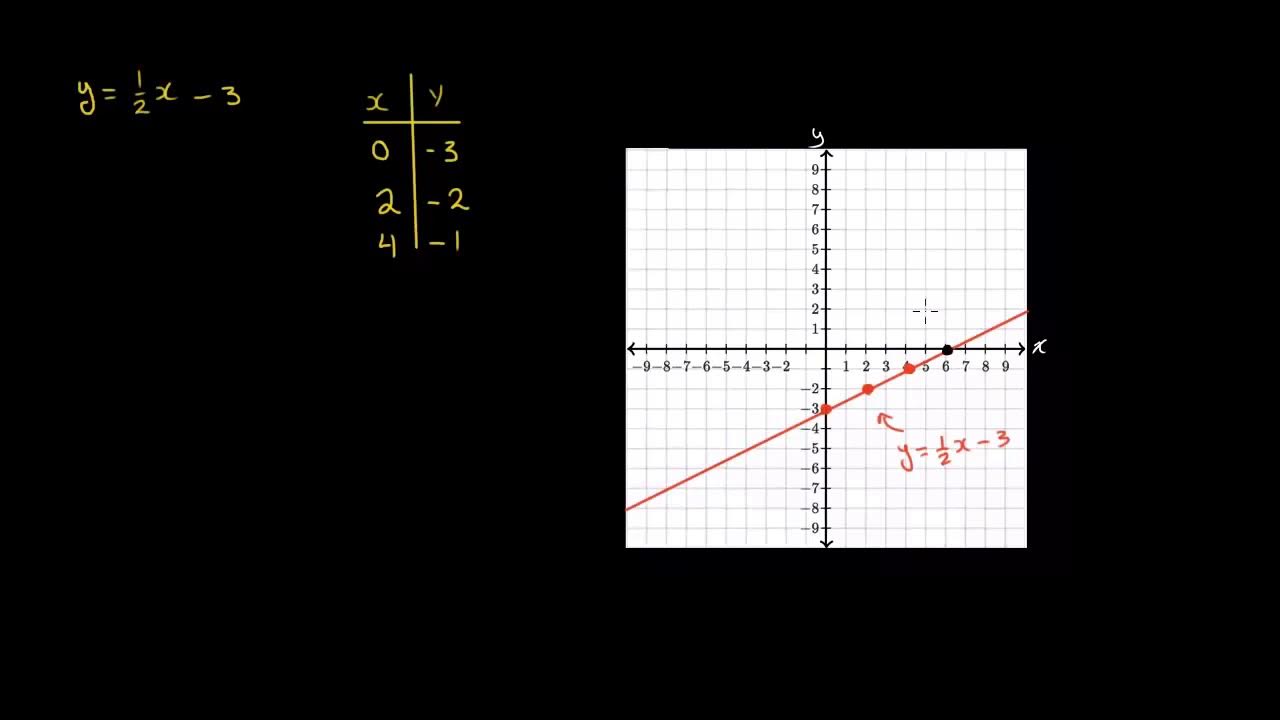
Introducción a las intersecciones con los ejes

Como graficar funciones racionales | Precálculo

Intersecciones de una función con los ejes X e Y / Función Lineal

PRIMER PROBLEMA FUNDAMENTAL GEOMETRÍA ANALÍTICA

Intersecciones con los ejes X y Y de una función cuadrática | puntos de corte con los ejes

Función Racional - Ejercicios Nivel 1 - Introducción
5.0 / 5 (0 votes)
