Understanding Shear Force and Bending Moment Diagrams

Summary

This educational video script offers a comprehensive guide to understanding shear force and bending moment diagrams, essential tools for mechanical and civil engineers analyzing beams under load. It explains the internal forces within a beam, including shear and normal forces, and how they manifest in different beam conditions like sagging or hogging. The script outlines the steps to determine these forces, including drawing free body diagrams, calculating reaction forces and moments, and constructing shear force and bending moment diagrams. It also covers sign conventions, the impact of various loads, and how to use equilibrium equations for statically determinate beams. The video concludes with practical examples and tips for predicting beam deformations based on bending moments.

Takeaways

• 📚 Shear force and bending moment diagrams are essential tools for engineers to analyze beams under various loads.
• 🔧 Internal forces in a beam consist of shear forces (vertical) and normal forces (along the beam's axis), which help maintain equilibrium.
• 📉 When a beam sags, the top experiences compression and the bottom experiences tension, leading to the development of bending moments.
• 📈 Shear forces and bending moments are represented as resultants on the beam's cross-section, simplifying the analysis of internal forces.
• 🏗️ Beams can be loaded with concentrated forces, distributed forces, or concentrated moments, and are supported in different ways like pinned, roller, or fixed supports.
• ⚖️ Reaction forces and moments at supports are determined using equilibrium concepts, leading to statically determinate or indeterminate beam analyses.
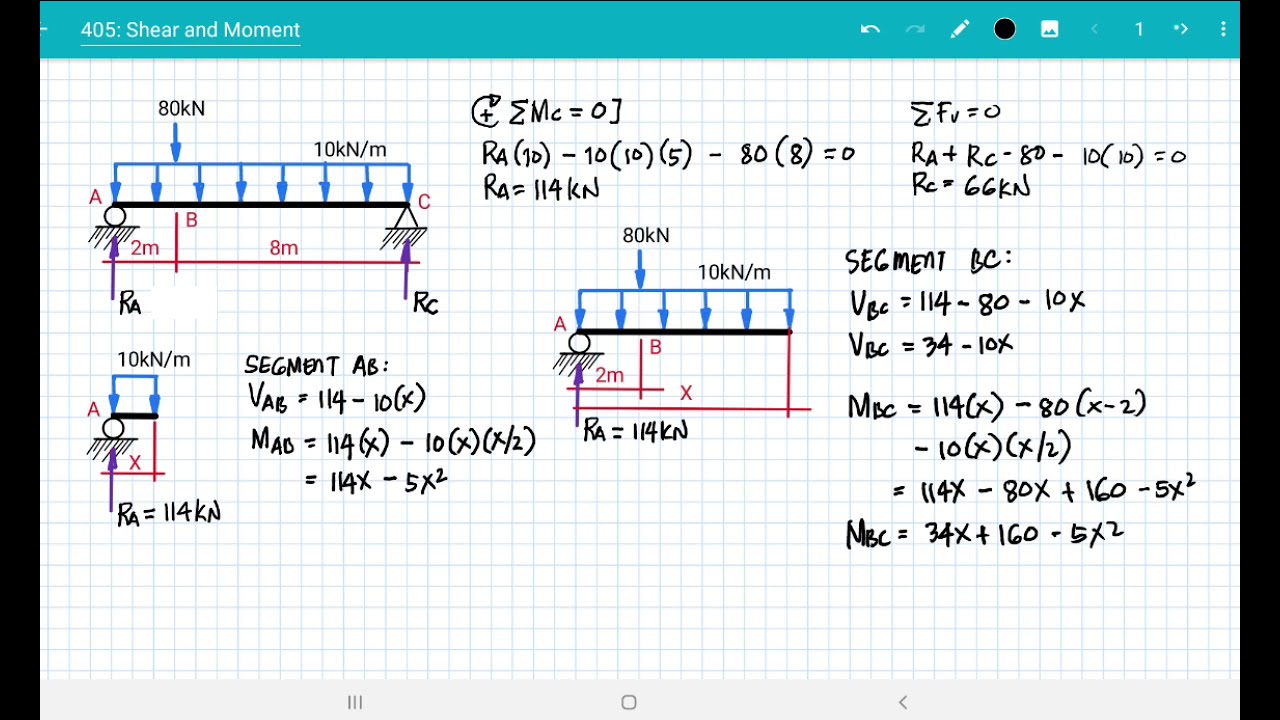
• 📉 The process of drawing shear force and bending moment diagrams involves calculating reaction loads and then determining internal forces at each beam location.
• 📌 Positive bending moments cause the lower section of the beam to be in tension, typically associated with sagging, while negative moments cause hogging.
• 🔍 Relationships between applied loads, shear forces, and bending moments can be used to construct or verify diagrams, such as the slope of the shear force curve being equal to the negative of the distributed load.
• 📊 The area under the shear force curve represents the change in bending moment, which is a useful method for diagram verification.

Q & A

What are shear force and bending moment diagrams?

Shear force and bending moment diagrams are graphical methods used by engineers to analyze the internal forces within a beam under various loads. They help visualize how a beam responds to different types of loading.

Why are shear forces and bending moments important in beam analysis?

Shear forces and bending moments are crucial for understanding the internal forces that develop within a beam when it is loaded. They are essential for determining the beam's structural integrity and predicting its behavior under load.

What are the two components of internal forces in a beam?

The two components of internal forces in a beam are shear forces, which are oriented in the vertical direction, and normal forces, which are oriented along the axis of the beam.

How do you represent the internal forces acting on a beam cross-section?

The internal forces acting on a beam cross-section are represented using two resultants: one shear force, which is a resultant of the vertical internal forces, and one bending moment, which is a resultant of the normal internal forces.

What are the different types of loads that can act on a beam?

Beams can be loaded by concentrated forces, distributed forces, and concentrated moments. These loads affect the shear force and bending moment diagrams and thus the beam's behavior.

What are the common types of beam supports and how do they affect the beam?

Common types of beam supports include pinned supports, roller supports, and fixed supports. Pinned supports allow rotation but prevent vertical and horizontal displacements, roller supports prevent vertical displacement but allow horizontal displacement and rotation, and fixed supports prevent all displacements and rotation.

What is a statically determinate beam and how is it different from a statically indeterminate beam?

A statically determinate beam is one where all the reaction forces and moments can be calculated using equilibrium equations. In contrast, a statically indeterminate beam has more unknowns than can be solved with the available equilibrium equations, requiring more complex methods to solve.

How do you determine the shear forces and bending moments within a beam?

To determine the shear forces and bending moments within a beam, you follow three main steps: draw a free body diagram of the beam, calculate the reaction forces and moments at the supports using equilibrium, and then calculate the internal shear forces and bending moments at each location along the beam.

What is the significance of the sign convention in shear force and bending moment diagrams?

The sign convention in shear force and bending moment diagrams is important for consistency and clarity in analysis. Applied forces are positive if they act downwards, and positive shear forces and bending moments are defined based on their orientation and effect on the beam's cross-section.

How can the relationships between applied loads, shear forces, and bending moments help in constructing diagrams?

The relationships between applied loads, shear forces, and bending moments can be used to derive equations for the shear force and bending moment curves. These relationships help in constructing accurate diagrams and performing sense checks by comparing calculated values with expected changes in the diagrams.

What insights can be gained from the shear force and bending moment diagrams about the deformed shape of a beam?

The shear force and bending moment diagrams can be used to predict the deformed shape of a beam. Positive bending moments indicate sagging, negative bending moments indicate hogging, and zero bending moments suggest a straight section of the beam.

Outlines

00:00

📚 Introduction to Shear Force and Bending Moment Diagrams

This paragraph introduces the concept of shear force and bending moment diagrams, essential tools for mechanical and civil engineers to analyze beams under various loads. The internal forces within a beam, comprising shear forces and normal forces, are explained. Shear forces act vertically, while normal forces can be compressive or tensile depending on the beam's curvature. The resultant forces are represented by shear forces and bending moments, which are crucial for understanding the beam's behavior under load. The paragraph also discusses different types of beam loadings and supports, including concentrated forces, distributed forces, pinned, roller, and fixed supports. The importance of reaction forces and moments at supports is highlighted, and the concept of statically determinate and indeterminate beams is introduced. The process of determining shear forces and bending moments involves drawing a free body diagram, calculating reaction forces and moments, and using equilibrium to find internal forces at any point along the beam.

05:04

🔍 Shear Force and Bending Moment Calculations

This paragraph delves into the process of calculating shear forces and bending moments for a beam with pinned and roller supports under the influence of concentrated forces. It explains the sign convention for applied forces and defines positive shear forces and bending moments. The example demonstrates how to draw a free body diagram, apply equilibrium equations to find reaction forces, and subsequently plot shear force and bending moment diagrams. The relationships between applied loads, shear forces, and bending moments are explored, with equations showing how the slope of the shear force curve relates to the distributed force and how the slope of the bending moment curve relates to the shear force. The integration of these equations is used to understand the area under loading diagrams and their impact on shear force and bending moment changes.

10:06

📈 Constructing Shear Force and Bending Moment Diagrams

This paragraph focuses on constructing shear force and bending moment diagrams for a beam with a distributed force and a concentrated force. It uses the free body diagram method to derive the equations for the bending moment curve and the shear force curve. The process involves differentiating the bending moment equation to find the shear force equation and then differentiating again to find the equation for the distributed force. The area method is introduced as a way to check the diagrams, where the area under the shear force curve equates to the change in bending moment. The paragraph also discusses how to handle discontinuities in the diagrams due to concentrated forces and moments, and how the equations apply across these discontinuities. The concept that a zero shear force indicates a local minimum or maximum in the bending moment curve is also highlighted.

15:10

🏗️ Analyzing Beams with Distributed Forces and Reaction Moments

The final paragraph examines a cantilever beam with a concentrated moment and a distributed force. It outlines the process of drawing a free body diagram and calculating the reaction forces and moments for a fully fixed support. The equilibrium equations are used to find the vertical and horizontal reaction forces and the reaction moment. The paragraph then describes how to calculate shear forces and bending moments along the beam, considering the effects of the reaction force and moment. The bending moment is particularly influenced by the reaction moment and the distributed force, leading to a quadratic equation for the bending moment in the affected section. The paragraph concludes with a discussion on how bending moment information can be used to predict the deformed shape of the beam, with sagging and hogging corresponding to positive and negative bending moments, respectively.

Keywords

💡Shear Force

Shear force refers to the internal forces in a beam acting in the vertical direction, caused by external loads. In the video, shear forces are described as one of the two main internal forces that maintain equilibrium in a beam under loading. For example, the shear force is calculated along the beam as the load distribution changes.

💡Bending Moment

A bending moment is the internal moment that results from the normal forces in a beam, causing it to bend. It is one of the key internal forces described in the video, and its magnitude and direction depend on the loading and support conditions. The video explains that bending moments cause sagging (positive moments) or hogging (negative moments) in a beam.

💡Equilibrium

Equilibrium refers to the condition where the sum of forces and moments in a system is zero, ensuring that the beam remains stable. The video emphasizes equilibrium as the foundation for calculating reaction forces and moments in a beam. For instance, the free body diagram is used to apply equilibrium equations to solve for unknowns in the structure.

💡Free Body Diagram

A free body diagram is a graphical representation that shows all external forces and moments acting on a system. In the video, this diagram is essential for solving problems related to shear forces and bending moments. The video explains how to use free body diagrams to isolate and analyze sections of the beam.

💡Reaction Forces

Reaction forces are the forces that develop at a beam's supports to counteract external loads, maintaining equilibrium. The video explains how to calculate these forces at pinned or roller supports, using equilibrium equations. For example, the reaction forces at points A and B are determined based on the applied loads.

💡Concentrated Load

A concentrated load is a load applied at a single point along the beam, causing localized effects on shear forces and bending moments. In the video, concentrated loads are introduced as one of the common ways beams are loaded, and examples are given where concentrated forces influence the shear force and bending moment diagrams.

💡Distributed Load

A distributed load is a load spread continuously over a length of the beam, causing varying internal forces along that section. The video discusses how distributed forces affect the slope of the shear force and bending moment diagrams and provides an example where the bending moment curve is derived for a beam under a distributed load.

💡Pinned Support

A pinned support allows rotation but prevents translation in both the vertical and horizontal directions. The video explains the role of pinned supports in beams, mentioning how these supports generate reaction forces but no reaction moments. An example is provided where a beam with pinned and roller supports is analyzed.

💡Roller Support

A roller support allows both horizontal movement and rotation but prevents vertical displacement. The video describes roller supports as a common type of beam support, and they are used in one of the beam examples to calculate shear forces and bending moments. Roller supports only generate vertical reaction forces.

💡Statically Determinate

A statically determinate structure is one in which the reaction forces and moments can be calculated solely using equilibrium equations. The video differentiates between statically determinate and indeterminate beams, focusing on simple examples where equilibrium equations are sufficient for solving the beam's internal forces.

Highlights

Shear force and bending moment diagrams are essential for analyzing beams under loading.

Shear forces and bending moments are internal forces that develop to maintain beam equilibrium.

Shear forces are oriented vertically, while normal forces are along the beam's axis.

Normal forces in a sagging beam are compressive at the top and tensile at the bottom.

Tensile and compressive normal forces produce moments but no net normal force.

Shear force and bending moment are used as resultants to represent internal forces on a beam cross-section.

Shear force and bending moment diagrams depend on beam loading and support conditions.

Beams can be loaded with concentrated forces, distributed forces, or concentrated moments.

Support types include pinned, roller, and fixed, each providing different degrees of restraint.

Reaction forces and moments at supports correspond to the degree of freedom restrained.

Statically determinate beams can have all reaction loads calculated using equilibrium equations.

Statically indeterminate beams require more complex methods beyond equilibrium equations.

The process of determining shear forces and bending moments involves three main steps: free body diagram, reaction force calculation, and internal force determination.

Sign convention for applied forces and moments is crucial for accurate diagram interpretation.

Shear force and bending moment diagrams can be constructed by moving a cut along the beam and applying equilibrium.

Relationships between applied loads, shear forces, and bending moments help in constructing diagrams.

The slope of the shear force curve is equal to the negative of the distributed force.

The slope of the bending moment curve is equal to the shear force at a given point.

Changes in shear force and bending moment can be determined by integrating the respective curves.

Shear force and bending moment diagrams can be checked using area equations and differentiation.

Concentrated forces cause jumps in the shear force diagram, while concentrated moments cause jumps in the bending moment diagram.

Shear force equal to zero indicates a local minimum or maximum in the bending moment curve.

Bending moment information can predict the deformed shape of a beam, showing where it sags or hogs.

Transcripts

Shear force and bending moment diagrams are powerful graphical methods that every mechanical

and civil engineer should know how to use to analyse a beam under loading.

In this video I’ll explain exactly how to master these diagrams, and we will see how

they can be used to understand how a beam is loaded.

I want to start by explaining what shear forces and bending moments actually are.

When a beam is loaded, internal forces develop within it to maintain equilibrium.

These internal forces have two components.

We have shear forces, oriented in the vertical direction.

And we also have normal forces, which are oriented along the axis of the beam.

If the beam is sagging, the top of the beam will get shorter, and so the normal forces

in the top of the beam will be compressive.

The bottom of the beam will get longer, and so the normal forces in the bottom of the

beam will be tensile.

Each of the tensile normal forces has a corresponding compressive force which is equal in magnitude

but opposite in direction.

As such these forces don’t produce a net normal force, but they do produce a moment.

This means that we can conveniently represent the internal forces acting on the beam cross-section

using just two resultants - one shear force, which is a resultant of the vertical internal

forces, and one bending moment, which is a resultant of the normal internal forces.

This is a very common way of representing the internal forces within a beam.

Drawing the shear force and bending moment diagrams is just figuring out what these internal

forces are at each location along the beam.

These resultant shear forces and bending moments will depend on the loads acting on the beam,

and the way in which the beam is supported.

Beams can be loaded in a number of ways, the most common being concentrated forces,

distributed forces, and concentrated moments.

Beams can also be supported in a number of different ways.

They can have pinned supports, roller supports, or be fully fixed, which each restrain the

beam in different ways.

Pinned supports prevent vertical and horizontal displacements but allow rotation.

Roller supports prevent vertical displacement but allow horizontal displacement and rotation.

Fixed supports prevent all displacements and rotation.

If a certain degree of freedom is restrained at a support, we will have a corresponding

reaction force or reaction moment at that location.

For example rotations are permitted for a pinned support, so there is no reaction moment,

but displacements in the vertical and horizontal directions are prevented, so we will have

horizontal and vertical reaction forces.

So how do you determine the shear forces and bending moments within a beam?

There are three main steps we need to follow.

First we draw a free body diagram of the beam.

This shows all of the applied and reaction loads acting on the beam.

The next step is to calculate the magnitude of the reaction forces and reaction moments

at all of the beam supports.

We do this using the concept of equilibrium.

To maintain equilibrium, all of the forces in the vertical and horizontal directions

should cancel each other out.

Similarly, all of the moments acting at every point along the beam should cancel each other out.

This gives us a set of simple equations we can solve to calculate the reaction forces

and moments.

If we can calculate all of the reaction loads using the three equilibrium equations, the

beam is said to be statically determinate.

For some beam configurations, like this one shown here, we won’t be able to calculate

all of the reaction loads because we have too many unknowns and not enough equilibrium

equations.

In this case the beam is said to be statically indeterminate.

This beam has 4 reaction forces, but we only have 3 equilibrium equations.

To solve this beam we would need to use slightly more complicated methods and consider boundary

conditions.

In this video I will only cover statically determinate cases, where we can use the equilibrium

equations to calculate all of the reaction loads.

Once we have calculated all of the reaction loads, the third and final step is to figure

out the internal shear forces and bending moments at every location along the beam.

To do this we will use the concept of equilibrium again.

If we cut our beam at any location, the internal forces and moments need to cancel out the

external forces and moments so that equilibrium is maintained.

This allows us to easily calculate the shear force and bending moment at each location

along the beam.

All we need to do is start from one side of the beam, and move the location of the cut

along the beam, calculating the shear forces and bending moments as we go.

Now is a good time to define the sign convention we will be using.

Applied forces will be positive if they are acting in the downwards direction.

For shear forces and bending moments, the positive sign convention will be as shown here.

If the beam is on the left side of our cut, shear forces pointing downwards will be positive.

If the beam is on the right side of our cut, shear forces pointing upwards will be positive.

Positive bending moments will be those that put the lower section of the beam into tension.

Another way to think about it is that bending moments which cause sagging of the beam are

positive, and those that cause hogging of the beam are negative.

Let's take a look at an example of a beam with pinned and roller supports, loaded by

two concentrated forces.

First we draw the free body diagram.

We can then use the equilibrium equations to determine the unknown reaction forces at

Point A and Point B.

The sum of the forces in the vertical direction is equal to zero, so R-A plus R-B is equal

to 15 plus 6.

Because H-A is the only horizontal force, it must be equal to zero.

We also know that the sum of the moments about any point along our beam must be zero.

Let's consider the moments about Point B. That gives us this equation, which we can

solve to determine that R-A is equal to 12.

By substituting R-A into the previous equation we can deduce that R-B is equal to 9.

Now that all of the external loads acting on the beam are defined, we can draw the shear

force and bending moment diagrams.

We will start from the left hand side of the beam.

Let's draw the free body diagram for a location immediately to the right of the 12 kN

reaction force.

To maintain equilibrium, the shear force must be equal to the reaction force.

We can draw this on our shear force diagram.

The shear force will be constant until we reach the next applied force.

The bending moment must be equal to the 12 kN reaction force multiplied by the

distance X to the reaction force.

This gives us the equation for a straight line, which we can draw on our

bending moment diagram.

We then repeat the process by moving the location of our cut further to the right.

This time we place the cut immediately after the 15 kN force, and we draw the free

body diagram again to determine the shear force and the bending moment.

We repeat this process until we have covered the full length of the beam.

We end up with the complete shear force and bending moment diagrams for the beam.

That example was a fairly simple one.

For cases with more complex loading, drawing the shear force and bending moment diagrams

can be more difficult.

There are relationships between the applied loads, shear forces and bending moments which

will help us better understand what our diagrams should look like.

Let's consider a beam loaded by an arbitrary distributed force.

We can zoom in to look at an infinitesimally small segment of the beam with a width equal

to D-X, and draw the free body diagram.

Over such a short section of the beam the distributed force can be assumed to be uniform,

and we can replace it with an equivalent concentrated force.

By applying the equilibrium equations to this free body diagram, it is possible to demonstrate

that the following relationships exist between the applied distributed force, the shear force

graph and the bending moment graph.

The quantity D-V over D-X is the slope of the shear force curve, and at a given point

along the beam it is equal to minus the distributed force.

Similarly D-M over D-X is the slope of the bending moment curve, and at a given point

it is equal to the shear force.

If we integrate the first equation, we can show that the change in shear force between

two points is equal to the area under the loading diagram between those two points.

And if we integrate the second equation we can show that the change in bending moment

between two points is equal to the area under the shear force curve.

This is really useful information we can use to help construct or sense check our shear

force and bending moment diagrams.

Let's take a look at an example.

This beam has an applied distributed force and a concentrated force.

Let’s quickly draw the shear force and bending moment diagrams.

By using the free body diagram method, we can show that the bending moment curve for

the section of the beam under the distributed force is defined by the quadratic equation

-4 X^2 + 34 X + 68.

If we differentiate this equation we get -8 X + 34, which based on the D-M over D-X

equation above we now know is the equation for the shear force curve in this section

of the beam.

If we differentiate again we get -8, which is the equation for the distributed force.

This is a great way to sense check your shear force and bending moment diagrams.

Another way of checking your diagrams is using the area equations I mentioned earlier.

The area under the shear force curve highlighted here is equal to 34 times 2, which is 68.

This is equal to the change in bending moment over this section of the beam.

We can also calculate the area under the shear force diagram for the beam section under the

distributed force.

The total area of this section is equal to 72.3 minus 12.3, which is 60.

This is equal to the change in bending moment of 60 kNm over this section of the beam.

Where concentrated forces are applied there is a sudden jump in the shear force diagram,

and where concentrated moments are applied there is a sudden jump in the bending moment diagram.

These equations will not be applicable across discontinuities in the diagrams.

One final observation we can make based on these equations is that when the shear force

is equal to zero, the bending moment curve will be at a local minimum or maximum.

Let’s look at one last example.

Here we have a cantilever with an applied concentrated

moment of 120 kNm and a distributed force of 6 kN/m.

Again we start by drawing the free body diagram.

Because the support is fully fixed, we have vertical and horizontal reaction forces R-A

and H-A, and a reaction moment M-A.

Let's look at our first equilibrium equation.

The sum of forces in the vertical direction is equal to zero.

In this case the only forces acting in the vertical direction are the reaction force

R-A and the distributed force, so R-A is equal to 6 times 3, which is 18.

H-A is the only force in the horizontal direction, so it must be equal to zero.

Next we can take the sum of the moments acting at point A. In calculating the moment caused

by a uniformly distributed force, you can remember that it is equal to a concentrated

force located in the middle point of the load.

This gives us M-A equals 21.

To calculate our shear forces and bending moments we will start on the left side of

the beam and move towards the right.

This is our first free body diagram.

The shear force calculation is easy, as we only need to consider the reaction force of 18 kN.

The bending moment needs to take into account the reaction moment and the reaction force.

At X equals zero the bending moment is equal to the reaction moment of 21 kNm.

As we move to the right we also need to consider the moment caused by the 18 kN reaction force.

This gives us the equation for a straight line.

We can then move our cut to the right of the concentrated moment.

The moment won't affect the shear force, which will remain constant at 18 kN until

we reach the distributed force.

But it does cause the bending moment to suddenly drop by 120 kNm.

After the drop, the bending moment is again defined by a straight line.

Things get a little more tricky when we reach the distributed force.

We can replace the uniformly distributed force by an equivalent concentrated force with a

magnitude of 6 multiplied by the length X over which the force is applied.

This force is located at a distance of X/2 from our cut.

We can then calculate the shear force and bending moment equations using the normal

approach.

The bending moment in this section of the beam is defined by a quadratic equation.

No loads are acting on the small one metre section to the right of the distributed force,

so shear forces and bending moments in that section will be equal to zero.

Although we can't calculate displacements from these diagrams, we can use the bending

moment information to predict the deformed shape of the beam.

Where the bending moment is positive the beam will be sagging, and where it is negative

it will be hogging.

Where the bending moment is zero the beam will be straight.

That will give us a deformed shape that looks something like this.

That's it for this quick look at shear forces and bending moments in beams.

I hope you learned something new, and if you enjoyed the video please don’t forget to subscribe!