Circumcenter of a Triangle
Summary
TLDRThis video script offers a clear guide to finding the Circumcenter of a triangle. It explains the process of locating the midpoint of each triangle's side and drawing perpendicular bisectors through these points. The intersection of these bisectors reveals the Circumcenter, a unique point equidistant from all triangle vertices. The script promises an enjoyable learning experience for viewers interested in geometry.
Takeaways
- 📐 The Circumcenter of a triangle is found by first locating the midpoints of its sides.
- 🔍 To find the midpoint, make two segments congruent by dividing one side of the triangle in half.
- 📏 The next step is to identify the perpendicular bisectors at each midpoint.
- 📍 A perpendicular bisector is a line that is perpendicular to a segment and passes through its midpoint.
- ⚓ All three perpendicular bisectors intersect at a single point, which is the Circumcenter.
- 🌐 The Circumcenter is equidistant from all three vertices of the triangle.
- 📊 This unique point is the same distance from each vertex, making it the center of a circle that passes through all three vertices.
- 🔄 The process involves geometric construction and understanding of perpendicular lines and midpoints.
- 📈 The Circumcenter has important properties in geometry, especially in the study of triangles and their circumcircle.
- 🔑 Knowing the Circumcenter can help in solving various geometric problems and understanding triangle symmetry.
- 🎓 This explanation is educational and aims to clarify the concept of the Circumcenter for viewers.
Q & A
What is the Circumcenter of a triangle?
-The Circumcenter of a triangle is the point where the perpendicular bisectors of the sides of the triangle intersect. It is equidistant from all three vertices of the triangle.
Why is it necessary to find the midpoint of each side of the triangle?
-Finding the midpoint of each side is necessary because the perpendicular bisectors of the sides are drawn through these midpoints, which will eventually intersect at the Circumcenter.
What is a perpendicular bisector?
-A perpendicular bisector is a line that is perpendicular to a segment and divides it into two equal parts, effectively bisecting the segment.
How many perpendicular bisectors are needed to find the Circumcenter?
-Three perpendicular bisectors are needed, one for each side of the triangle, to find the Circumcenter.
What is unique about the distance of the Circumcenter from the vertices of the triangle?
-The unique quality of the Circumcenter is that it is equidistant from all three vertices of the triangle, meaning the distance to each vertex is the same.
Can the Circumcenter be inside the triangle?
-No, the Circumcenter is always outside the triangle for acute and obtuse triangles. However, for a right-angled triangle, the Circumcenter lies on the hypotenuse, and for an equilateral triangle, it is inside at the center.
What is the significance of the Circumcenter in geometry?
-The Circumcenter is significant as it is the center of the circumscribed circle (circumcircle) around the triangle, and it provides a common point of reference for the distances to all vertices.
How does the Circumcenter relate to the centroid and orthocenter of a triangle?
-The Circumcenter is related to the centroid and orthocenter as they are all special points in a triangle that have unique geometric properties and are used for different purposes in geometry.
Can the Circumcenter be used to determine the type of triangle?
-While the Circumcenter itself does not directly determine the type of triangle, its location relative to the triangle can provide clues. For example, if the Circumcenter is inside the triangle, it indicates an acute triangle.
What is the relationship between the Circumcenter and the incenter of a triangle?
-The Circumcenter and incenter are both centers of a triangle, but they are defined differently. The Circumcenter is the point where the perpendicular bisectors intersect, while the incenter is where the angle bisectors intersect and is the center of the inscribed circle (incircle).
Is there a specific method to find the Circumcenter if the triangle is not equilateral?
-Yes, for non-equilateral triangles, the method involves finding the midpoint of each side, drawing the perpendicular bisectors through these midpoints, and finding their intersection point, which is the Circumcenter.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
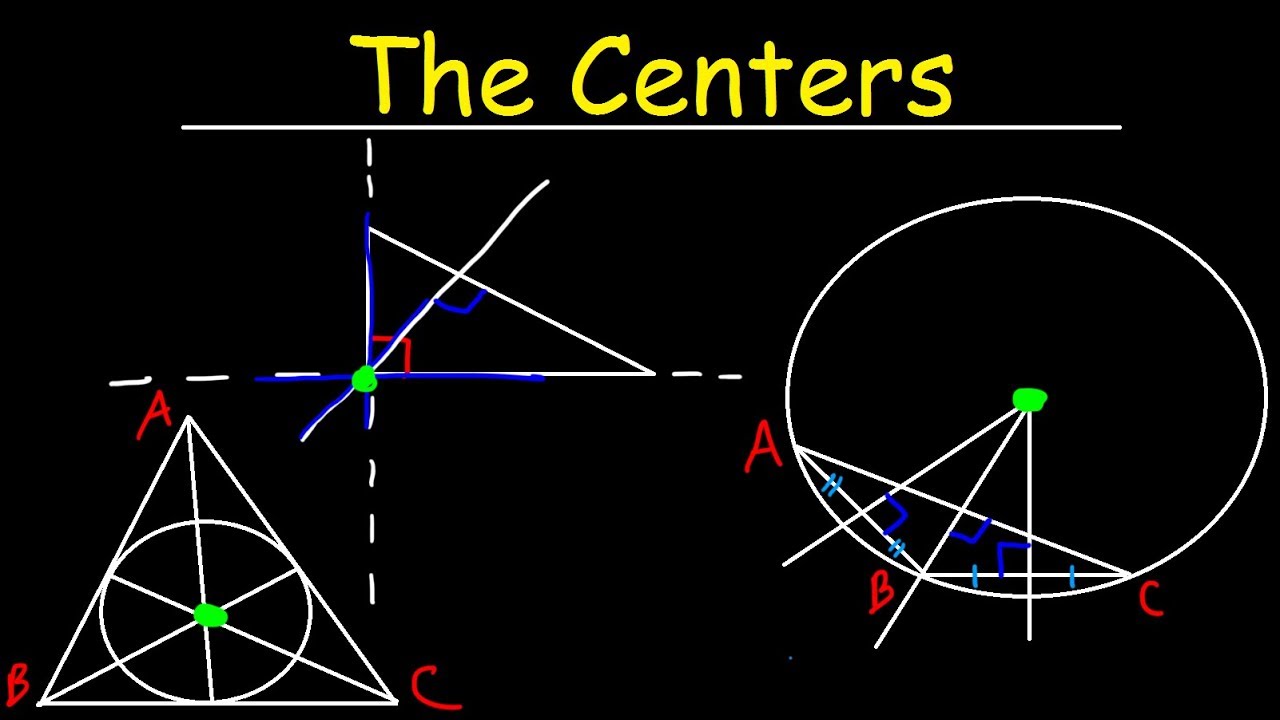
Incenter, Circumcenter, Orthocenter & Centroid of a Triangle - Geometry

Bisectors of Triangles // GEOMETRY
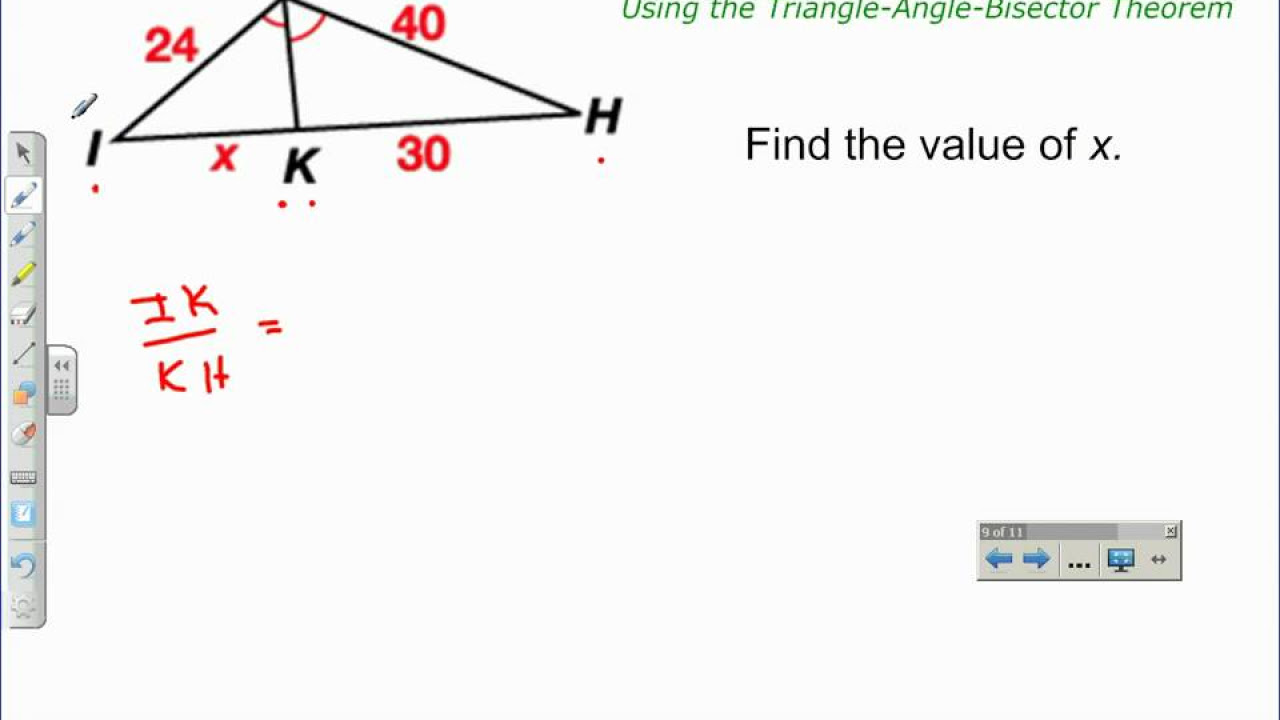
Triangle-Angle-Bisector Theorem

Triangle Centers Identification

The Ultimate Tutorial On Targeting The Right Audience On Facebook & Instagram For Jewelry Brands

Solving Equations Transformable into Quadratic Equations
5.0 / 5 (0 votes)
