Vértice de una parábola
Summary
TLDREl script ofrece una clase sobre cómo encontrar el vértice de una parábola o función cuadrática. Se ilustra cómo las parábolas pueden abrir hacia arriba o abajo y se enfatiza la importancia del vértice como el punto más alto o bajo de la parábola. Se explica el proceso para determinar las coordenadas del vértice utilizando la fórmula -b/2a, y se practica con ejemplos para que los estudiantes puedan aplicar estos conceptos. El video concluye con un ejercicio práctico y una invitación a explorar más contenido en el canal.
Takeaways
- 📚 Los estudiantes aprenden a encontrar el vértice de una parábola o función cuadrática.
- 📈 La importancia del vértice se destaca como el punto más alto o más bajo de la parábola y como el punto que la divide en dos partes iguales.
- 🔍 Se ilustra cómo las parábolas que abren hacia arriba tienen un vértice más bajo y las que abren hacia abajo, un vértice más alto.
- 📉 Se menciona que las parábolas pueden tener diferentes posiciones iniciales pero lo importante es su dirección de apertura.
- 📝 Se describe el proceso de encontrar puntos en una función, reemplazando 'x' con valores específicos para calcular 'y'.
- 🔢 Se explica que para encontrar el vértice de una función cuadrática, se utiliza la fórmula -b/(2a) para la coordenada x.
- 📐 Se da un ejemplo práctico de cómo ordenar una función cuadrática y encontrar sus coeficientes a, b y c.
- 🧮 Se muestra el cálculo paso a paso para encontrar la coordenada x del vértice, utilizando los coeficientes de la función.
- 📉 Se procede a encontrar la coordenada y del vértice, sustituyendo la coordenada x en la función original.
- 📝 Se enfatiza la importancia de realizar operaciones matemáticas en el orden correcto: primero potencias, luego multiplicaciones y finalmente sumas y restas.
- 📚 Se invita a los estudiantes a practicar con un ejercicio similar para reforzar los conceptos aprendidos.
Q & A
¿Qué es el vértice de una parábola y por qué es importante?
-El vértice de una parábola es el punto más alto o más bajo de la parábola, y es importante porque divide la parábola en dos partes iguales, una que va hacia la izquierda y otra hacia la derecha.
¿Cómo se identifican las parábolas que abren hacia arriba y las que abren hacia abajo?
-Las parábolas que abren hacia arriba suelen tener una forma de 'U' invertida, mientras que las que abren hacia abajo tienen una forma de 'U' normal. En el script, las parábolas que abren hacia arriba están marcadas en rojo y las que abren hacia abajo en azul.
¿Cómo se encuentra la coordenada x del vértice de una función cuadrática?
-Para encontrar la coordenada x del vértice de una función cuadrática, se utiliza la fórmula -b/(2a), donde 'a' es el coeficiente de la x al cuadrado y 'b' es el coeficiente de la x.
¿Qué es necesario hacer antes de encontrar el vértice de una función cuadrática?
-Antes de encontrar el vértice, es necesario asegurarse de que la función esté ordenada, con el término de x al cuadrado a un lado y los demás términos al otro lado.
¿Cómo se encuentra la coordenada y del vértice una vez que se conoce la coordenada x?
-Para encontrar la coordenada y del vértice, se reemplaza el valor de x en la función cuadrática y se resuelve la ecuación para encontrar el valor de y.
¿Qué es una función cuadrática y cómo se diferencia de otras funciones?
-Una función cuadrática es una función de la forma f(x) = ax^2 + bx + c, donde 'a', 'b' y 'c' son constantes y 'a' no es cero. Se diferencia de otras funciones por tener un término x al cuadrado.
¿Cómo se grafican las funciones y por qué es importante ubicar puntos con valores de x específicos?
-Para graficar funciones, se le dan valores a x y se encuentran los correspondientes valores de y. Es importante ubicar puntos específicos para visualizar la forma de la función y determinar características como el vértice.
¿Por qué es útil saber cómo encontrar el vértice de una parábola en matemáticas?
-Conocer cómo encontrar el vértice de una parábola es útil porque proporciona información sobre el punto máximo o mínimo de la función, lo cual es importante en problemas de optimización y análisis de datos.
¿Cómo se resuelve el ejercicio propuesto al final del script para encontrar el vértice de otra función cuadrática?
-Para resolver el ejercicio, se identifican los valores de 'a', 'b' y 'c' en la función dada, se utiliza la fórmula -b/(2a) para encontrar la coordenada x del vértice, y luego se reemplaza x en la función para encontrar la coordenada y.
¿Dónde puedo encontrar más información sobre funciones y cómo se enseña esta unidad en el canal del instructor?
-Puedes encontrar más información sobre funciones en el canal del instructor, en el enlace de la descripción del video o en la tarjeta que aparece en la parte superior del video.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

FUNCIÓN CUADRÁTICA: Explicación Completa y Cómo Graficarla
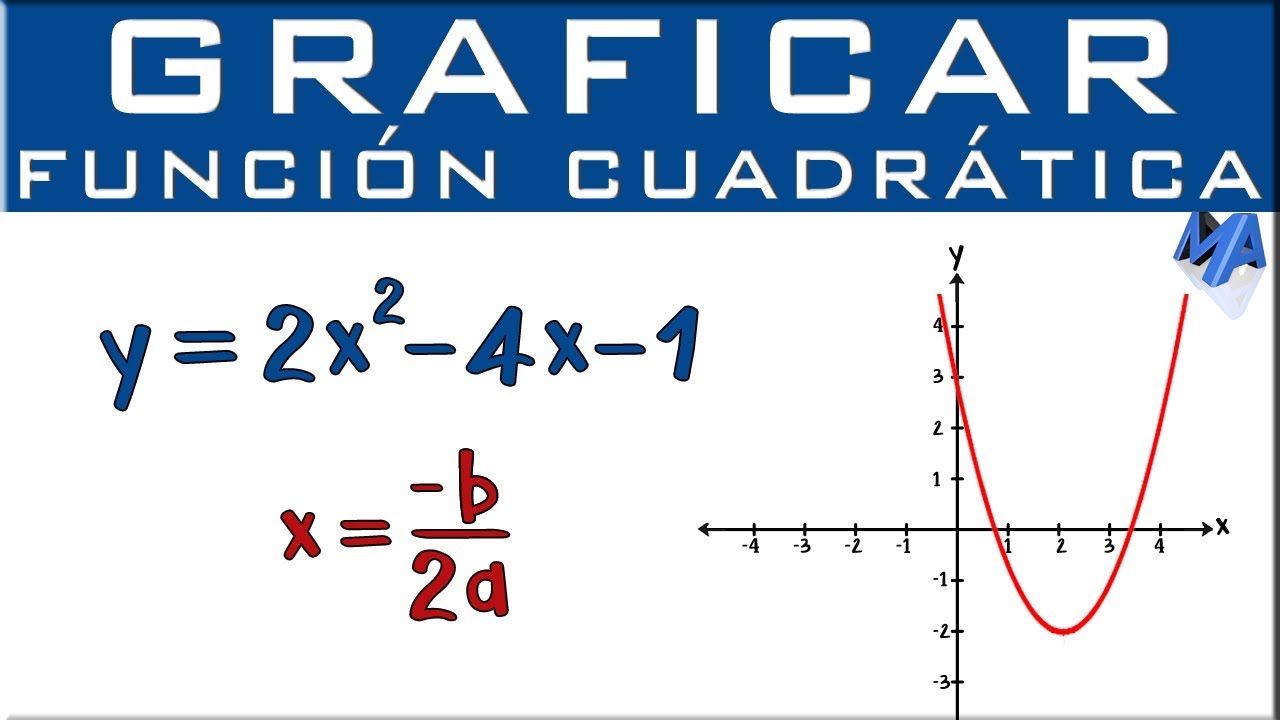
Gráfica de la función cuadrática o de segundo grado

Función cuadrática. Gráfico: hallando vértice, raíces, ordenada al origen. Parte1/7
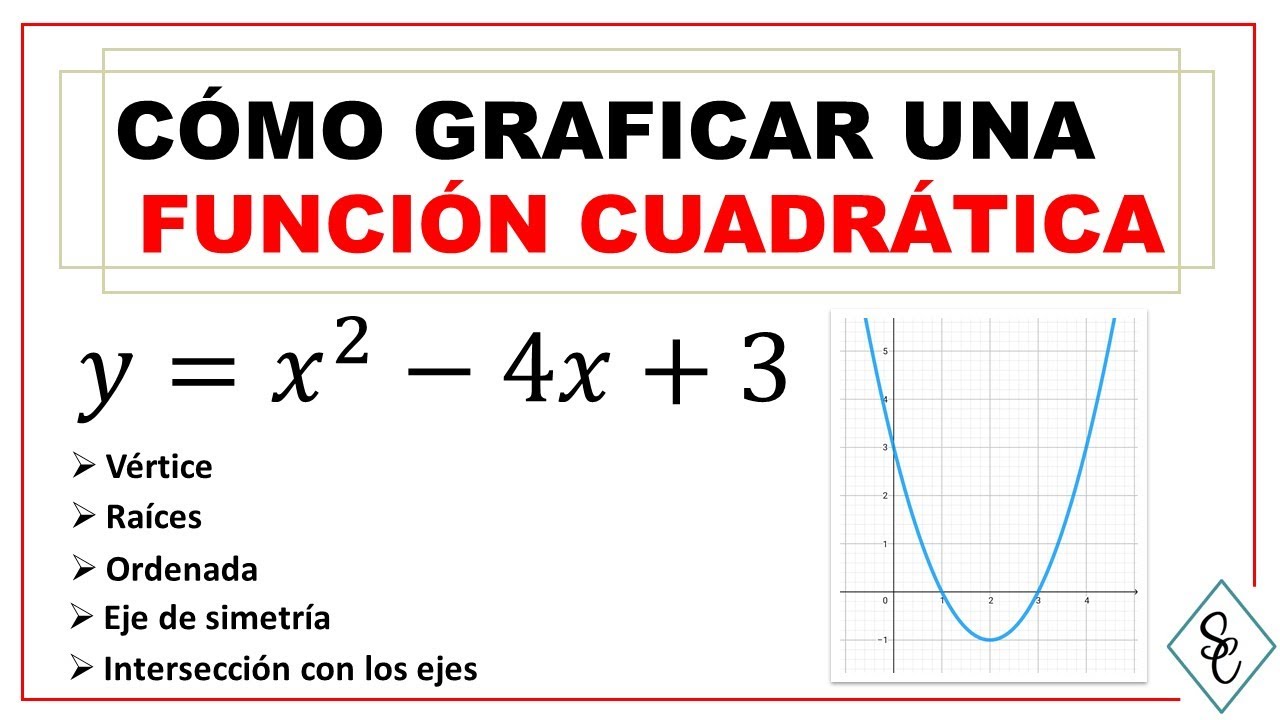
FUNCIÓN CUADRÁTICA - Cómo graficarla calculando todos sus puntos mas importante

GRAFICAR FUNCIONES CUADRÁTICAS Super facil

ANÁLISIS DE FUNCIONES CUADRÁTICAS - Ejercicio 2
5.0 / 5 (0 votes)
