4 Dogs Problem: The Inefficient Solution (3b1b SoME#2 Entry)
Mathing
15 Aug 202211:59
Summary
TLDR在这段视频中,作者分享了一个有趣的数学谜题:四只狗从正方形的顶点出发,以恒定速度相互追逐,最终在中心相遇。尽管作者花了几周时间才找到自己的解法,但发现网上的解答更简洁。通过实验和图表,作者解释了狗的螺旋运动路径,并证明了它们所走的曲线总长与原正方形的边长相等。视频强调了解决问题过程的重要性,并鼓励观众用不同的方法解决一个问题,而不是单一方法解决多个问题。
Takeaways
- 🧩 一道花费了很长时间才解决的有趣谜题,但最终发现更简单的解决方案。
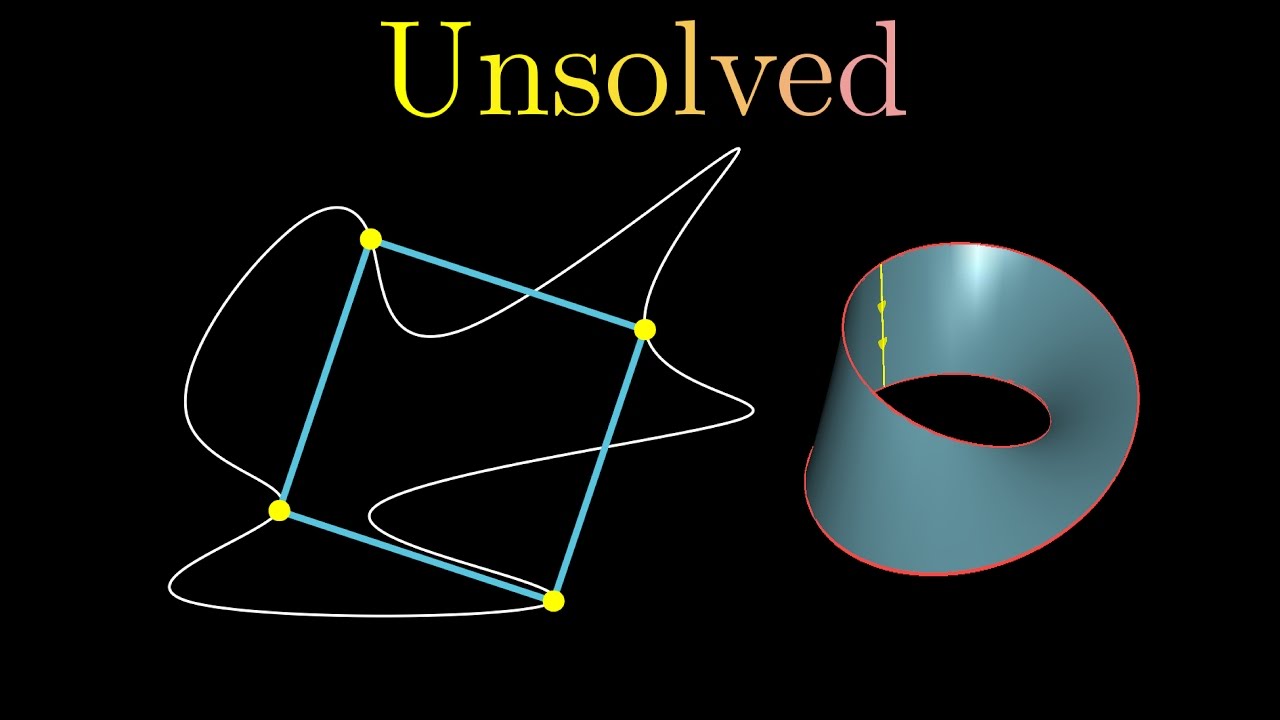
- 🕵️♂️ 四只狗分别位于边长为一单位的正方形的顶点,并以每秒一单位的速度分别朝向下一只狗移动。
- 🔄 狗的路径不是圆形,而是向中心慢慢螺旋状移动。
- 🧠 假设狗的反应速度有滞后时间 t 秒,以观察它们的路径变化。
- 📉 建立图表,将每一步的距离变化和中间正方形的边长绘制在坐标轴上。
- 🔬 通过图表可以发现路径长度和中间正方形边长之间的关系。
- 📏 即使没有螺旋方程,仍可以通过图表找到狗移动的总距离。
- 📈 证明在 t 接近零时,图表曲线是直线,且斜率为常数。
- 🧮 计算得出总路径长度等于初始正方形的边长。
- ✨ 强调解决问题的过程和思维方法的重要性,比单纯找到答案更有意义。
Q & A
视频开头提到的谜题是什么?
-视频开头提到的谜题是关于四只狗坐在边长为1个单位的正方形顶点上,且每只狗都以1单位/秒的速度朝向下一只狗移动的问题。
谜题中四只狗的移动速度是多少?
-四只狗的移动速度是1单位/秒。
四只狗的移动方向是怎样的?
-第一只狗总是朝向第二只狗移动,第二只狗总是朝向第三只狗移动,第三只狗总是朝向第四只狗移动,第四只狗总是朝向第一只狗移动。
四只狗最终会在什么地方相遇?
-四只狗最终会在正方形的中心相遇。
四只狗的路径会是什么形状?
-四只狗的路径是螺旋状逐渐向中心靠拢。
如何通过实验模拟狗的路径?
-通过设定狗有一个t秒的延迟时间,每隔t秒调整一次方向,可以模拟出螺旋状的路径。随着t值减小,路径逐渐逼近实际情况。
如何测量狗的螺旋路径的长度?
-通过建立一个图表,在x轴上标记每一步的距离,在y轴上标记每一步形成的中间正方形的边长,可以找到狗走到中心的总距离。
如何证明原始情况下的路径是一条直线?
-通过计算延迟情况下的路径斜率,发现其斜率趋于负一,证明了原始路径是一条直线。
图表中y轴为0时对应的x轴值是什么意义?
-y轴为0时对应的x轴值是狗走到中心的总距离,在本例中等于1单位。
视频的核心主题是什么?
-视频的核心主题是解谜的过程本身,而非结果。通过不同方法解决一个问题比单一方法解决多个问题更有价值。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
Rate This
★
★
★
★
★
5.0 / 5 (0 votes)
相关标签
数学谜题复杂路径数学之美智力挑战狗的运动追逐问题路径计算数学思维解决方法趣味数学