GENERATING PATTERNS IN SERIES || GRADE 10 MATHEMATICS Q1
Summary
TLDRIn this video, Monica explains the concepts of finite and infinite series, and how to express a series using Sigma notation. She begins by defining a series as the sum of the terms of a sequence and provides examples of both finite and infinite series. Monica demonstrates how to calculate the sum of the first few terms in a sequence and introduces the concise Sigma notation for expressing series. The video includes detailed examples, helping viewers understand how to apply these mathematical concepts in various scenarios.
Takeaways
- 🔢 A series is the sum of the terms of a sequence.
- 🔍 A finite series, also called a partial sum, has a specific number of terms.
- ∞ An infinite series continues without end, summing terms indefinitely.
- 🧮 The sum of the first 'n' terms of a sequence is denoted by 'S_n'.
- 💡 Sigma notation (Σ) is used to express series concisely.
- 🔄 In Sigma notation, the Greek letter Σ represents summation, and the expression below it indicates the starting value.
- ➕ The upper limit of the summation is shown above the Σ symbol.
- 📏 Examples of sequences include 1, 3, 5, 7, 9, 11 and their sum is a series.
- 🔄 Finite series examples include the sum of terms like 1 + 3 + 6 + 10 + 15, which results in specific values.
- 🔍 Sigma notation can express complex series such as fractions or squared terms, simplifying the notation for summing sequences.
Q & A
What is a series?
-A series is the sum of the terms of a sequence.
What is the difference between a finite series and an infinite series?
-A finite series is the sum of a specific number of terms in a sequence, while an infinite series is the sum of all terms in an infinite sequence.
How is a series expressed in Sigma notation?
-A series can be expressed in Sigma notation by using the Greek letter Sigma (Σ) to indicate the summation of terms, specifying the lower and upper limits and the expression for the terms.
What is an example of converting a sequence to a series?
-If we have the sequence 1, 3, 5, 7, 9, 11, the series would be the sum of these terms: 1 + 3 + 5 + 7 + 9 + 11.
How do you calculate the sum of the first six terms of the sequence 1, 3, 5, 7, 9, 11?
-The sum of the first six terms is calculated as 1 + 3 + 5 + 7 + 9 + 11 = 36.
What is a partial sum in the context of series?
-A partial sum, or finite series, is the sum of the first n terms of a sequence.
How do you find the partial sum S_3 for the sequence 1, 3, 6, 10, 15?
-S_3 is the sum of the first three terms: 1 + 3 + 6 = 10.
What is the sum of the first four terms of the sequence 5, 15, 25, 35?
-The sum of the first four terms is 5 + 15 + 25 + 35 = 80.
How is the series 1 + 1/2 + 1/3 + 1/4 + 1/5 expressed in Sigma notation?
-The series is expressed as Σ (1/k) from k=1 to k=5.
How do you express the series 1^2 + 2^2 + 3^2 + ... + n^2 in Sigma notation?
-The series is expressed as Σ (k^2) from k=1 to k=n.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Calculo Integral 03: Notación Sigma. Sigma notation.

GRADE 7 MATH | SETS NAMING A SET, FINITE, INFINITE, NULL, CARDINALITY, AND SUBSETS | TAGALOG

Convergence and Divergence: The Return of Sequences and Series

Pre-Calculus : GEOMETRIC SEQUENCE

Notasi Sigma Matematika Kelas 11 • Part 1: Pengertian Notasi Sigma
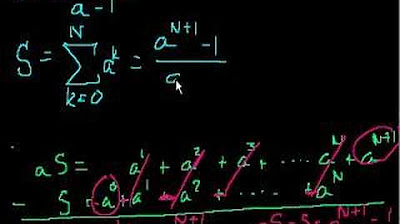
Sequences and series (part 2)
5.0 / 5 (0 votes)
