pola bilangan kelas 8 part 1 (mudah)

Summary

In this educational video, Abi Mu'ith introduces grade 8 students to number patterns in mathematics, covering various sequences such as odd numbers, square numbers, Fibonacci numbers, and more. He explains how these patterns appear in everyday life, like house numbers and book arrangements. The video explores different types of number sequences, including arithmetic and geometric sequences, as well as methods to predict the next terms. Practical examples and problems help students understand how to identify and solve number pattern problems, making learning mathematics engaging and easier for students.

Takeaways

• 😀 The video discusses mathematical patterns, specifically number patterns, aimed at grade 8 students in the first semester of mathematics.
• 😀 The importance of recognizing patterns in everyday life is emphasized, with examples such as house numbering and seating arrangements.
• 😀 Key objectives include generalizing number patterns, determining the next term in sequences, and solving problems related to object configuration sequences.
• 😀 Various types of number patterns are introduced, such as odd numbers, even numbers, square numbers, and Fibonacci numbers.
• 😀 The triangular number pattern is explained with the visual arrangement of balls forming a triangle.
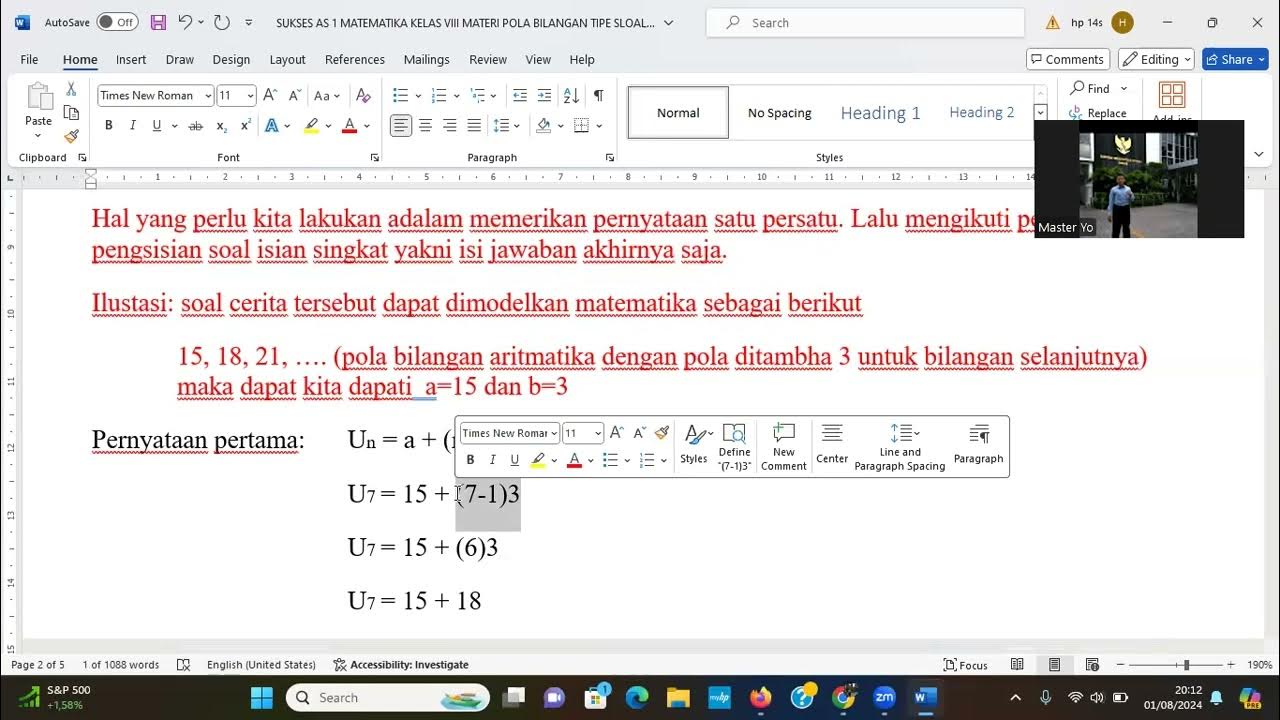
• 😀 Arithmetic and geometric sequences are defined, highlighting their respective characteristics: arithmetic sequences involve constant addition or subtraction, while geometric sequences involve constant multiplication or division.
• 😀 A method for determining the next term in a number sequence is demonstrated using the example of increasing by 2, illustrating how to find the next three terms.
• 😀 The importance of understanding patterns is reinforced through practical examples like chair arrangement in libraries and number patterns in books.
• 😀 The script explains the concept of solving number patterns in object configurations and the role of equations in number sequences.
• 😀 The concept of powers of numbers and unit digits, such as the unit digit of 3 raised to large powers, is explored through the example of calculating 3^200.

Q & A

What is the main focus of the lesson in the video?

The main focus of the lesson is understanding number patterns, including how to identify and generalize patterns in number sequences and object configurations for grade 8 students.

Can you give an example of how number patterns appear in everyday life?

Number patterns can be seen in everyday life, such as house numbering in a housing complex where odd and even numbers alternate or in book numbering patterns in libraries.

What is an arithmetic sequence?

An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant, either by addition or subtraction of the same number.

What defines a geometric sequence?

A geometric sequence is a sequence of numbers where each term is found by multiplying the previous term by a fixed number (common ratio), or by dividing it by a fixed number.

How do you determine the next term in an arithmetic sequence?

To determine the next term in an arithmetic sequence, simply add or subtract the constant difference between terms to the last known term.

What is a square number pattern?

A square number pattern consists of numbers that are perfect squares, such as 1, 4, 9, 16, and so on. These numbers are the result of squaring natural numbers.

Explain how to identify a triangular number pattern.

A triangular number pattern involves a sequence of numbers that can form an equilateral triangle when represented with dots or objects. The sequence starts with 1, 3, 6, 10, and so on.

How is the next number in the Fibonacci sequence found?

In the Fibonacci sequence, each term is the sum of the two preceding terms. For example, 0, 1, 1, 2, 3, 5, 8, 13, and so on.

What is the importance of generalizing number patterns?

Generalizing number patterns helps to create formulas or equations that can predict future terms in the sequence, making it easier to solve related problems and apply them in real-world situations.

How can you find the unit digit of a large power like 3^200?

To find the unit digit of large powers, observe the repeating cycle of unit digits in powers of the base number. For example, powers of 3 follow a cycle of unit digits: 3, 9, 7, 1. By finding the remainder when dividing the exponent by the cycle length, you can determine the unit digit.