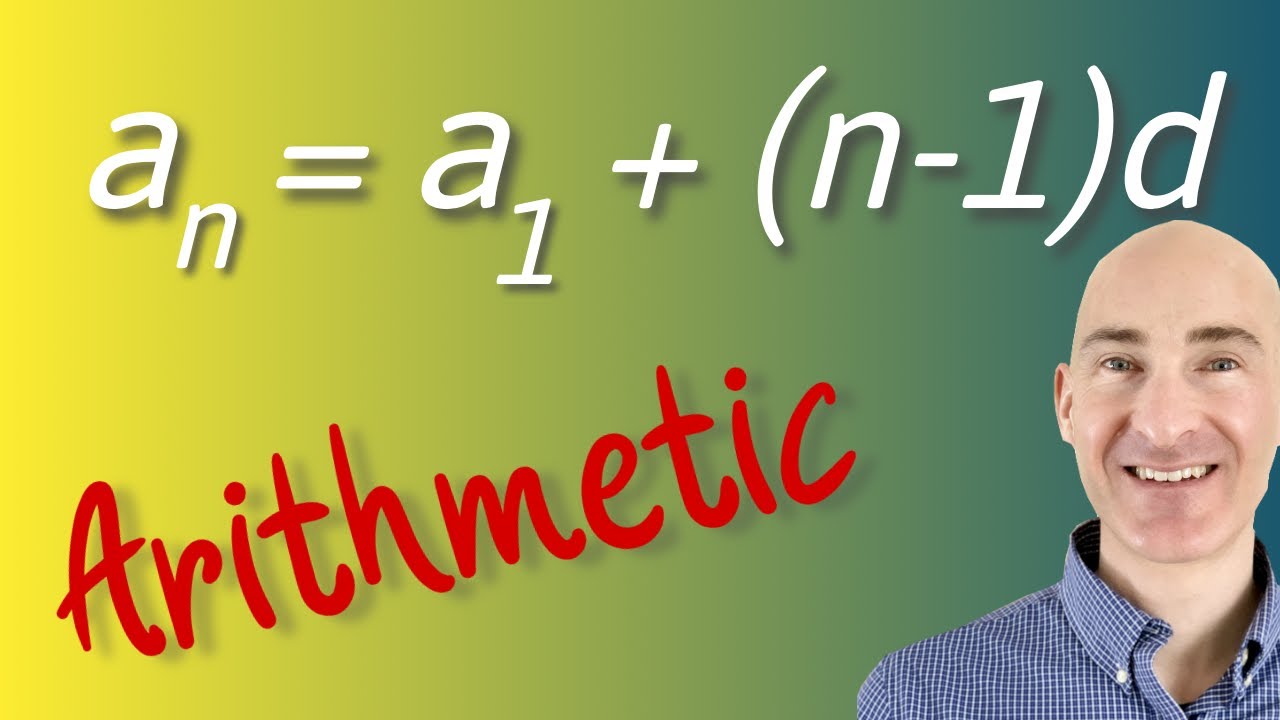Barisan dan Deret Aritmatika #matematika kelas 8

Summary

This tutorial introduces the concept of arithmetic sequences, explaining their structure and how to calculate specific terms and sums. The video covers essential formulas, including the general term formula (UN = a + (n-1) * B) and the sum formula (SN = n/2 * (2a + (n-1) * B)). Through practical examples, such as calculating the 40th term of a sequence and determining the total savings after two years with a fixed increase each month, the tutorial provides clear steps and applications of these formulas. It’s a useful guide for anyone learning arithmetic sequences.

Takeaways

• 😀 Introduction to Arithmetic Sequences, explaining the concept of a series of numbers that follow a specific pattern based on addition or subtraction.
• 😀 Arithmetic sequences have a constant difference, denoted by 'b', which is the key to calculating subsequent terms.
• 😀 The basic formula to calculate the n-th term (Un) in an arithmetic sequence is: Un = a + (n - 1) * b, where 'a' is the first term and 'b' is the common difference.
• 😀 Another useful formula for calculating the sum of the first 'n' terms (Sn) in an arithmetic sequence is: Sn = n/2 * (2a + (n - 1) * b).
• 😀 An example problem is given where the 40th term of an arithmetic sequence is calculated using the known first few terms.
• 😀 For the sequence 7, 5, 3, 1, the common difference (b) is -2, and the formula is applied to find the 40th term, resulting in -71.
• 😀 A second example is provided, where a child saves money in the bank with increasing monthly deposits, starting at Rp 50,000 and increasing by Rp 5,000 each month.
• 😀 The total number of months for the savings is 24 (2 years), and the common difference is Rp 5,000.
• 😀 The total savings after 2 years is calculated using the sum formula for an arithmetic sequence, resulting in Rp 2,500,000.
• 😀 The script emphasizes the practical use of arithmetic sequences in real-world scenarios, such as calculating savings over time.

Q & A

What is an arithmetic sequence?

An arithmetic sequence (or series) is a sequence of numbers where the difference between consecutive terms is constant. This difference is called the 'common difference'.

What is the formula for the nth term of an arithmetic sequence?

The formula for the nth term of an arithmetic sequence is: UN = a + (n - 1) * B, where UN is the nth term, 'a' is the first term, 'n' is the term number, and 'B' is the common difference.

How do you calculate the common difference in an arithmetic sequence?

The common difference (B) is calculated by subtracting the first term from the second term: B = U2 - U1.

What is the formula to find the sum of the first n terms of an arithmetic sequence?

The formula to find the sum of the first n terms of an arithmetic sequence is: Sn = n/2 * (2a + (n - 1) * B), where Sn is the sum of the first n terms, 'a' is the first term, 'n' is the number of terms, and 'B' is the common difference.

What does 'a' represent in the formulas for arithmetic sequences?

In the formulas for arithmetic sequences, 'a' represents the first term of the sequence.

What is the significance of the number 40 in the example of calculating the 40th term?

In the example, the number 40 represents the position of the term in the sequence, i.e., the 40th term. The goal is to find the value of the term at that position using the arithmetic sequence formula.

How is the 40th term calculated in the example, and what is the result?

In the example, the 40th term is calculated using the formula UN = a + (n - 1) * B. With the first term a = 7, common difference B = -2, and n = 40, the 40th term is calculated as: UN = 7 + (40 - 1) * -2 = -71.

What does 'Sn' represent in the formula for the sum of the first n terms?

In the formula for the sum of the first n terms, 'Sn' represents the sum of the first n terms in the arithmetic sequence.

In the example of the child saving money in the bank, how is the common difference (B) calculated?

The common difference (B) is calculated by subtracting the first savings amount from the second. In this case, B = 55,000 - 50,000 = 5,000.

How is the total amount of money saved by the child after two years (24 months) calculated?

The total amount saved is calculated using the sum formula Sn = n/2 * (2a + (n - 1) * B). With the first savings a = 50,000, common difference B = 5,000, and n = 24 (months), the total savings after 2 years is calculated to be 2,500,000.