Garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran

Summary

This video tutorial explains how to calculate the lengths of external and internal common tangents between two circles. The video demonstrates two examples: one involving larger and smaller circles with radii of 8m and 3m, and the other with radii of 6m and 2m. The presenter outlines the formulas to determine the tangents, using simple arithmetic and providing step-by-step solutions. The tutorial is straightforward and aims to make learning these concepts easy, with a clear focus on practical application and understanding for students studying geometry.

Takeaways

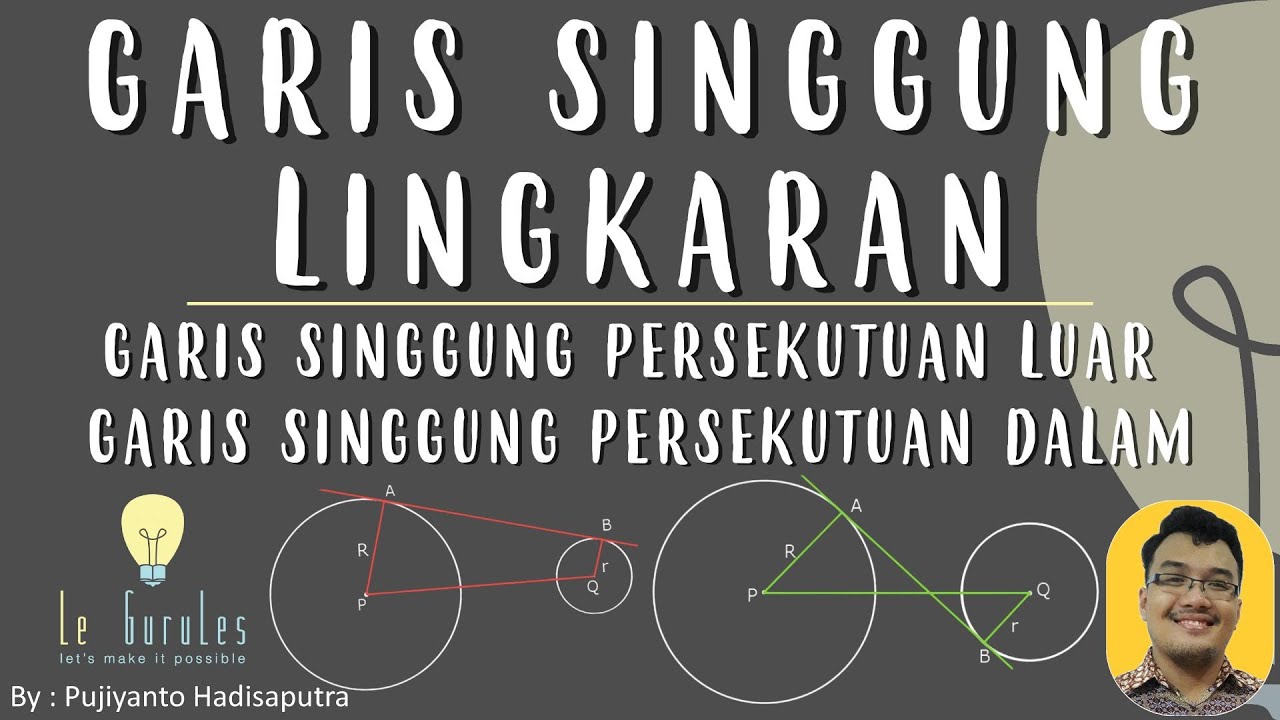
• 😀 Introduction to the topic: The video focuses on tangent lines, specifically external and internal common tangents of two circles.
• 😀 The concept of the external common tangent is explained using a diagram with two circles—one large and one small.
• 😀 The formula for calculating the length of the external common tangent is explained: √(X² - (R1 - R2)²), where X is the distance between the centers of the circles, and R1 and R2 are their radii.
• 😀 For the first example, the large circle has a radius of 8 meters, and the small circle has a radius of 3 meters. The distance between their centers is 13 meters.
• 😀 The calculation for the external tangent results in a length of 12 meters, with all measurements in meters.
• 😀 The next part of the video explains the internal common tangent, using a similar diagram of two circles with radii of 6 meters (large circle) and 2 meters (small circle), and the distance between their centers is 17 meters.
• 😀 The formula for the internal common tangent is also discussed: √(X² - (R1 + R2)²), where X is the distance between the centers of the circles, and R1 and R2 are their radii.
• 😀 For the second example, the calculation for the internal tangent results in a length of 15 meters.
• 😀 Both formulas for calculating the tangents are straightforward and can be applied to any similar problem involving two circles.
• 😀 The video concludes with a friendly reminder to like, subscribe, comment, and share the video, with hopes that it provides valuable educational content.

Q & A

What is the topic of the video?

The video discusses tangent lines and the concepts of internal and external common tangents between two circles.

What is the formula for calculating the length of the external common tangent?

The formula is: √(d² - (R1 - R2)²), where d is the distance between the centers of the two circles, and R1 and R2 are the radii of the two circles.

What values were used to calculate the length of the external common tangent?

In the example, the distance between the centers (d) was 13 meters, the radius of the larger circle (R1) was 8 meters, and the radius of the smaller circle (R2) was 3 meters.

How do you calculate the length of the external tangent using the provided example?

First, square the distance between the centers: 13² = 169. Then, subtract the square of the difference between the radii: (8 - 3)² = 25. Finally, subtract 25 from 169, and take the square root: √(169 - 25) = √144 = 12 meters.

What is the formula for calculating the length of the internal common tangent?

The formula for the internal common tangent is: √(d² - (R1 + R2)²), where d is the distance between the centers of the two circles, and R1 and R2 are the radii of the two circles.

What values were used to calculate the length of the internal common tangent?

In the example, the distance between the centers (d) was 17 meters, the radius of the larger circle (R1) was 6 meters, and the radius of the smaller circle (R2) was 2 meters.

How do you calculate the length of the internal tangent using the provided example?

First, square the distance between the centers: 17² = 289. Then, add the radii: 6 + 2 = 8, and square that: 8² = 64. Finally, subtract 64 from 289, and take the square root: √(289 - 64) = √225 = 15 meters.

Why are there different formulas for the internal and external common tangents?

The difference in formulas arises from the positioning of the circles relative to each other. The external tangent is calculated using the difference in the radii, while the internal tangent uses the sum of the radii.

How important is it to correctly choose which circle's radius to assign as R1 or R2 in the formulas?

It is important to correctly assign the radii because it determines how you approach the calculation. However, the answer will be the same regardless of which radius is assigned to R1 or R2 as long as the correct difference or sum is used in the formula.

What can we conclude from the example about calculating tangents?

We can conclude that the calculations for both internal and external common tangents are straightforward, as long as you correctly apply the appropriate formula and use the correct distance and radii values.