Exam Hack | CIE AS Maths | P1 | Function Transformations Question

Summary

This tutorial delves into the world of function transformations, focusing on shifting, stretching, and reflecting functions such as quadratics and trigonometric graphs. The speaker provides a clear explanation of how different transformations—vertical and horizontal shifts, amplitude changes, and reflections—affect graph behavior. Using various examples and illustrations, the content explores concepts like the impact of adding or subtracting values to functions and how to graph these changes. The speaker emphasizes the practical understanding of functions, offering insight into their role in real-world scenarios like business and society, and encourages further learning through downloadable worksheets.

Takeaways

• 😀 Transformations of functions involve shifting, stretching, reflecting, and changing their amplitude or period.
• 😀 Adding or subtracting a constant to the function shifts the graph vertically (up or down) along the y-axis.
• 😀 Adding or subtracting a constant to the x-input of the function shifts the graph horizontally (left or right) along the x-axis.
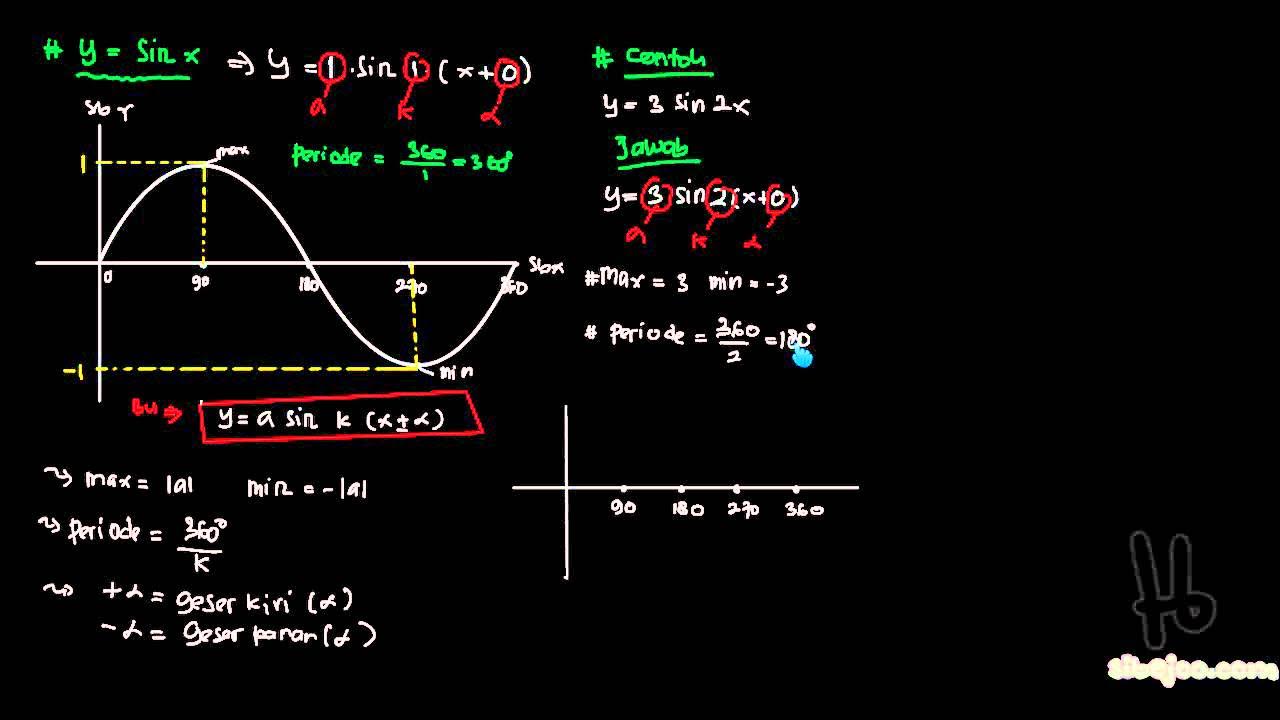
• 😀 When the function is multiplied by a constant, it stretches or compresses the graph vertically, affecting the amplitude for trigonometric functions.
• 😀 When the x-input is multiplied by a constant (e.g., sine of 2x), it compresses or stretches the graph horizontally, altering the period of trigonometric functions.
• 😀 Reflecting the function in the x-axis (multiplying by -1) flips the graph vertically, while reflecting in the y-axis (replacing x with -x) flips the graph horizontally.
• 😀 For quadratic functions, completing the square helps in identifying the vertex and understanding its transformations, such as shifts in the x and y directions.
• 😀 Shifting a graph horizontally involves adjusting the input to the function; adding to x moves it left, and subtracting moves it right.
• 😀 A clear understanding of the transformations requires practicing with different types of functions (polynomial, trigonometric, etc.).
• 😀 These mathematical functions and transformations can be applied beyond math, affecting real-life scenarios like business, technology, and personal development.
• 😀 The importance of understanding functions extends beyond math class, providing insight into how systems work in the world and in society.

Q & A

What is the main concept being explained in the video?

The video focuses on the concept of function transformations, explaining how to shift, stretch, reflect, and manipulate functions in both the x and y directions.

What does adding or subtracting a constant inside the function do?

Adding or subtracting a constant inside the function affects the graph's position along the x-axis. Adding shifts the graph to the left, while subtracting shifts it to the right.

How does adding or subtracting a constant outside the function affect the graph?

Adding or subtracting a constant outside the function shifts the graph vertically. Adding shifts it upwards, and subtracting shifts it downwards.

What happens when the function is stretched or compressed vertically?

A vertical stretch occurs when the output of the function is multiplied by a constant greater than 1, increasing the amplitude of the graph. A vertical compression occurs when the constant is between 0 and 1, reducing the amplitude.

How does a horizontal stretch or compression affect a function?

A horizontal stretch happens when the input of the function is multiplied by a constant greater than 1, elongating the graph along the x-axis. A horizontal compression happens when the constant is between 0 and 1, shortening the graph along the x-axis.

What does reflecting a function in the x-axis look like?

Reflecting a function in the x-axis involves changing the sign of the output values. This means that all the y-values of the graph are flipped, making the graph appear upside down.

How do you reflect a function in the y-axis?

Reflecting a function in the y-axis involves changing the sign of the input values. This means that all positive x-values are replaced with their negative counterparts, flipping the graph horizontally.

How do you apply a transformation to the cosine function?

For the cosine function, transformations can involve stretching or compressing the graph horizontally by changing the input (such as cos(θ/2) for a stretch), or vertically by multiplying the function by a constant (like 2*cos(θ) for a vertical stretch). Additionally, you can shift the graph vertically by adding a constant, such as cos(θ) + 3.

What is the effect of multiplying a function by a negative number?

Multiplying a function by a negative number reflects it across the x-axis, effectively flipping the graph vertically. For example, if f(x) = x², then -f(x) = -x² would flip the graph upside down.

How do you determine the equation of a transformed quadratic function?

To determine the equation of a transformed quadratic function, identify the shifts in the x and y directions, as well as any stretches or compressions. For example, if the graph of y = x² is shifted left by 3 units and down by 4 units, the equation becomes y = (x + 3)² - 4.