Fungsi Trigonometri (Part 1) Grafik Fungsi Sinus
Summary
TLDRThis video tutorial provides a comprehensive guide on graphing trigonometric functions, focusing on sine, cosine, and tangent. It covers essential concepts such as special angles, quadrant rules, and the basic sine wave, explaining its amplitude, period, and the effects of transformations. The tutorial also delves into horizontal shifts, vertical stretching, and how altering the coefficients of trigonometric functions affects their graphs. Through practical examples and visual aids, viewers will learn how to plot and analyze these functions with precision and understand key transformations like shifting and scaling, essential for mastering trigonometry.
Takeaways
- 😀 Memorize the values of trigonometric functions for special angles like 0°, 30°, 45°, 60°, and 90°.
- 😀 Understand the sign rules for trigonometric functions in each quadrant (ASTC: All Students Take Calculus).
- 😀 In Quadrant I, all functions (sine, cosine, tangent) are positive.
- 😀 In Quadrant II, only sine is positive, while cosine and tangent are negative.
- 😀 In Quadrant III, only tangent is positive, while sine and cosine are negative.
- 😀 In Quadrant IV, only cosine is positive, while sine and tangent are negative.
- 😀 The sine function starts at 0°, peaks at 90°, returns to 0° at 180°, reaches its minimum at 270°, and completes one full period at 360°.
- 😀 The amplitude of the sine graph is 1 by default, meaning it oscillates between 1 and -1.
- 😀 Shifting the sine graph horizontally can be done by adding or subtracting a constant inside the argument (e.g., `sin(x + 30°)`).
- 😀 Changing the coefficient of the variable inside the sine function (e.g., `sin(2x)`) compresses the period, making it half of the original period.
- 😀 The period of the sine function can be calculated using the formula `Period = 360° / frequency`, so for `sin(2x)` the period is 180°, and for `sin(3x)` the period is 120°.
Q & A
What are the special angles that need to be memorized for understanding trigonometric functions?
-The special angles that need to be memorized are 0°, 30°, 45°, 60°, and 90°. These are essential for determining the values of sine, cosine, and tangent for these angles in various quadrants.
How do we determine the signs of sine, cosine, and tangent in different quadrants?
-The signs of sine, cosine, and tangent in different quadrants can be remembered using the acronym ASTC (All Students Take Calculus), where: In quadrant I, all functions are positive; in quadrant II, only sine is positive; in quadrant III, only tangent is positive; and in quadrant IV, only cosine is positive.
How do you determine the value of sin(150°)?
-To determine sin(150°), first recognize that 150° is in quadrant II. The reference angle is 30° (since 180° - 150° = 30°), and sine is positive in quadrant II. Therefore, sin(150°) = sin(30°), which is 1/2.
What is the value of cos(225°), and how is it determined?
-cos(225°) is in quadrant III, where cosine is negative. The reference angle is 45° (since 225° - 180° = 45°), so cos(225°) = -cos(45°) = -√2/2.
How do we calculate tan(330°)?
-To calculate tan(330°), recognize that 330° is in quadrant IV, where tangent is negative. The reference angle is 30° (since 360° - 330° = 30°), so tan(330°) = -tan(30°) = -√3/3.
What is the general process for graphing trigonometric functions like sin(x)?
-To graph a trigonometric function like sin(x), you need to fill out a table with key values of x (such as 0°, 30°, 60°, 90°, etc.), calculate their corresponding sine values, and then plot these points on the graph. The graph of sin(x) will be a smooth wave that oscillates between -1 and 1, with a period of 360°.
What is the amplitude of the graph of sin(x), and what does it represent?
-The amplitude of the graph of sin(x) is the maximum value of the function, which is 1, and the minimum value, which is -1. The amplitude represents the height of the wave from the middle axis (usually y = 0) to the peak or trough of the wave.
What happens to the graph of a sinusoidal function when it is transformed by adding a constant inside the function, like sin(x + 30°)?
-When a sinusoidal function is transformed by adding a constant inside the function (like sin(x + 30°)), the graph is shifted horizontally. In this case, adding 30° shifts the graph 30° to the left. The value inside the sine function controls the phase shift of the graph.
How does the period of a sinusoidal function change if the function is multiplied by a coefficient, like sin(2x)?
-When the function is multiplied by a coefficient inside the argument (like sin(2x)), the period of the graph decreases. The period of sin(x) is 360°, and for sin(2x), the period becomes 360°/2 = 180°. This causes the graph to complete one cycle in 180°.
What effect does multiplying the sine function by a coefficient outside the argument (e.g., 2sin(x)) have on the graph?
-Multiplying the sine function by a coefficient outside the argument (e.g., 2sin(x)) affects the amplitude of the graph. The amplitude is multiplied by the coefficient, so the new amplitude becomes 2, meaning the graph will oscillate between -2 and 2 instead of -1 and 1.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Matematika SMA - Trigonometri (3) -Sistem Kuadran, Relasi Sudut Trigonometri (A)

PERBANDINGAN TRIGONOMETRI (PART 1) SINUS, COSINUS, TANGEN, SECAN, COSECAN, COTANGEN

✅INTEGRALES trigonométricas con POTENCIAS [𝙚𝙣 4 𝙋𝙖𝙨𝙤𝙨 😎🫵💯 ] Cálculo Integral
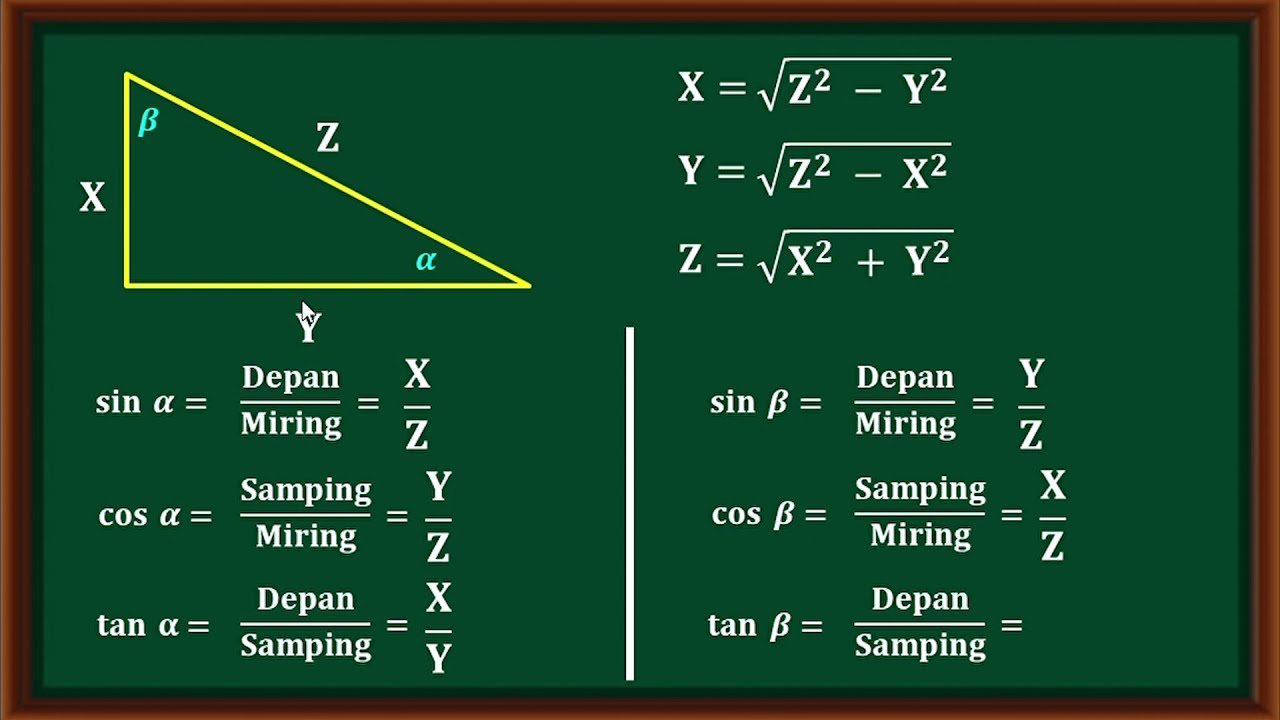
Materi dan soal pembahasan Perbandingan trigonometri dari suatu sudut pada segitiga siku-siku.

TRIGONOMETRI - Ukuran Sudut dan Perbandingan Trigonometri

[Math 20] Lec 3.4 Fundamental Identities (1 of 2)
5.0 / 5 (0 votes)