3.1 Bilangan Real (Pendahuluan)

Summary

This video lecture explores the concept of real numbers, discussing their definition and properties. The speaker highlights different perspectives, such as real numbers being the distance between points on a continuous line, or as a combination of rational and irrational numbers. The lecture dives into the subsets of real numbers, like integers, natural numbers, and whole numbers. It also touches on the relationship between real numbers and imaginary numbers, introducing complex numbers as a combination of both. The content emphasizes the interconnectedness of real numbers and their role in mathematical operations and further studies in complex analysis.

Takeaways

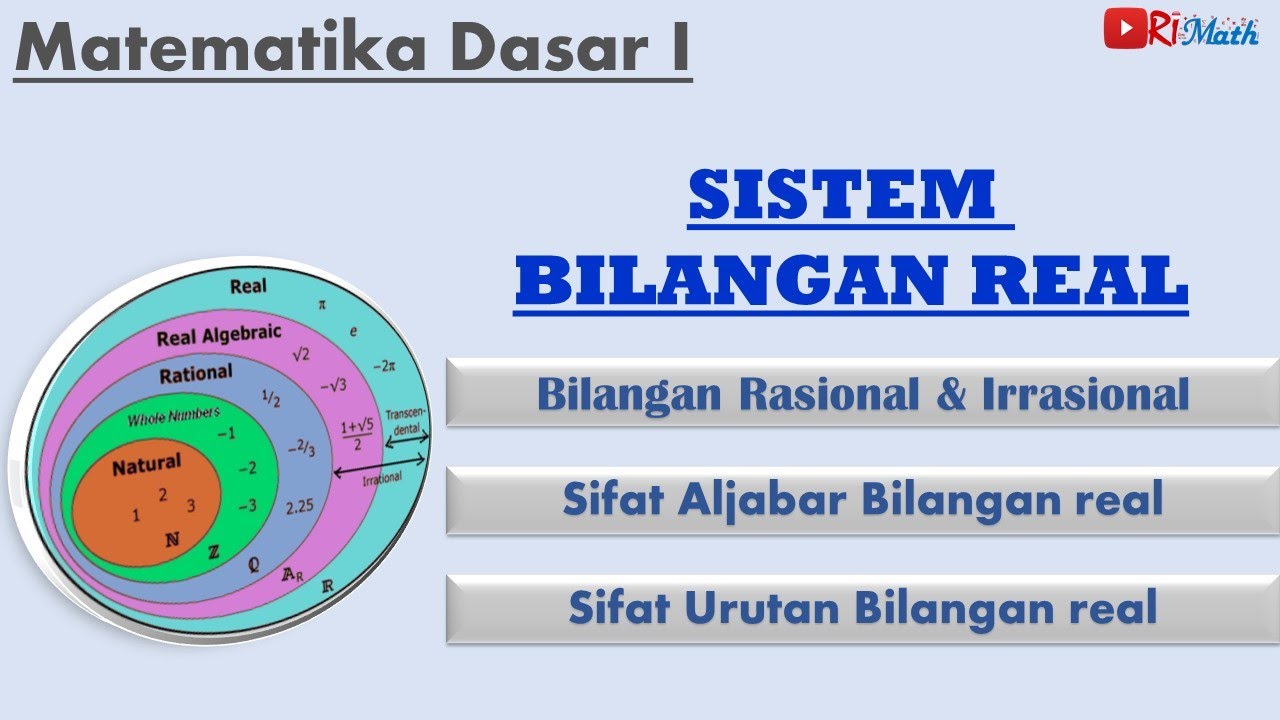
• 😀 The real numbers are defined in various ways, including as the distance between two points on a continuous number line or as a union of rational and irrational numbers.
• 😀 Real numbers are often described as all the numbers found on the real number line, which includes both positive and negative values.
• 😀 Rational numbers can be expressed as fractions with integer numerators and denominators, and their decimal expansions are either finite or repeating.
• 😀 Irrational numbers, unlike rational numbers, cannot be expressed as fractions, and their decimal expansions are non-repeating and non-terminating.
• 😀 The set of rational numbers is divided into subsets, such as integers (Z), and further into natural numbers (N), whole numbers (W), and negative integers.
• 😀 The natural numbers (N) start from 1 and go upwards, while the whole numbers (W) include zero along with natural numbers.
• 😀 A negative integer set is denoted by Z-, and the set of whole numbers excluding zero is denoted by W.
• 😀 Real numbers, when involved in operations like square roots, may result in imaginary numbers. For example, the square root of a negative number is defined as an imaginary number.
• 😀 Imaginary numbers are defined as numbers that, when squared, result in a negative value, like the square root of -1, denoted as i.
• 😀 When real and imaginary numbers are combined, they form complex numbers, which can be represented in the Cartesian plane with real numbers on the x-axis and imaginary numbers on the y-axis.

Q & A

What is the definition of real numbers?

Real numbers are values that represent the distance between two points on a continuous number line. They can also be defined as the union of rational and irrational numbers, or simply as positive or negative numbers with decimal digits.

How are real numbers represented on the number line?

Real numbers are represented on the number line with zero at the center, extending positively to the right and negatively to the left. This includes all numbers in the continuous line, from positive values like 1, 2, and 3, to negative values like -1, -2, and so on.

What are the two main categories of real numbers?

Real numbers are divided into two main categories: rational numbers and irrational numbers. Rational numbers can be expressed as fractions, while irrational numbers cannot.

What are rational numbers?

Rational numbers are numbers that can be expressed as the quotient of two integers, meaning they can be written in the form of a fraction, where both the numerator and the denominator are integers. Examples include numbers like 1/2, 3/4, and 9.11.

What are irrational numbers?

Irrational numbers are real numbers that cannot be expressed as fractions. Their decimal representations are non-repeating and non-terminating. Examples include numbers like √2, π, and e.

What is the difference between rational numbers and irrational numbers in terms of decimal representation?

The decimal representation of rational numbers either terminates or repeats in a pattern, whereas the decimal representation of irrational numbers is non-repeating and infinite.

What are integers, and how are they related to rational numbers?

Integers are a subset of rational numbers that include all positive and negative whole numbers, as well as zero. They are denoted by the symbol 'Z'.

What is the set of natural numbers, and how does it relate to integers?

Natural numbers, denoted by 'N', are the set of positive integers starting from 1. They are a subset of integers and are used for counting.

What happens when we take the square root of negative numbers?

The square root of a negative number does not produce a real number. Instead, it results in an imaginary number. For example, the square root of -9 is expressed as 3i, where 'i' is the imaginary unit.

How are imaginary numbers and real numbers related?

Imaginary numbers are numbers that involve the square root of negative values, represented by 'i'. When combined with real numbers, they form complex numbers, which can be represented in the complex plane with real numbers on the x-axis and imaginary numbers on the y-axis.