MEASURES OF DISPERSION || MATHEMATICS IN THE MODERN WORLD

Summary

This video explains statistical measures of variability, such as range, variance, and standard deviation, which help assess the spread of data. It covers the calculation methods for both population and sample variance and standard deviation, providing a clear step-by-step example. The video also includes an application example comparing battery life consistency across three companies using standard deviation. This informative guide helps viewers understand how to compute and interpret these measures of data dispersion, making complex concepts more accessible.

Takeaways

• 😀 Measures of variability, like range, variance, and standard deviation, help us understand how spread out the data is.
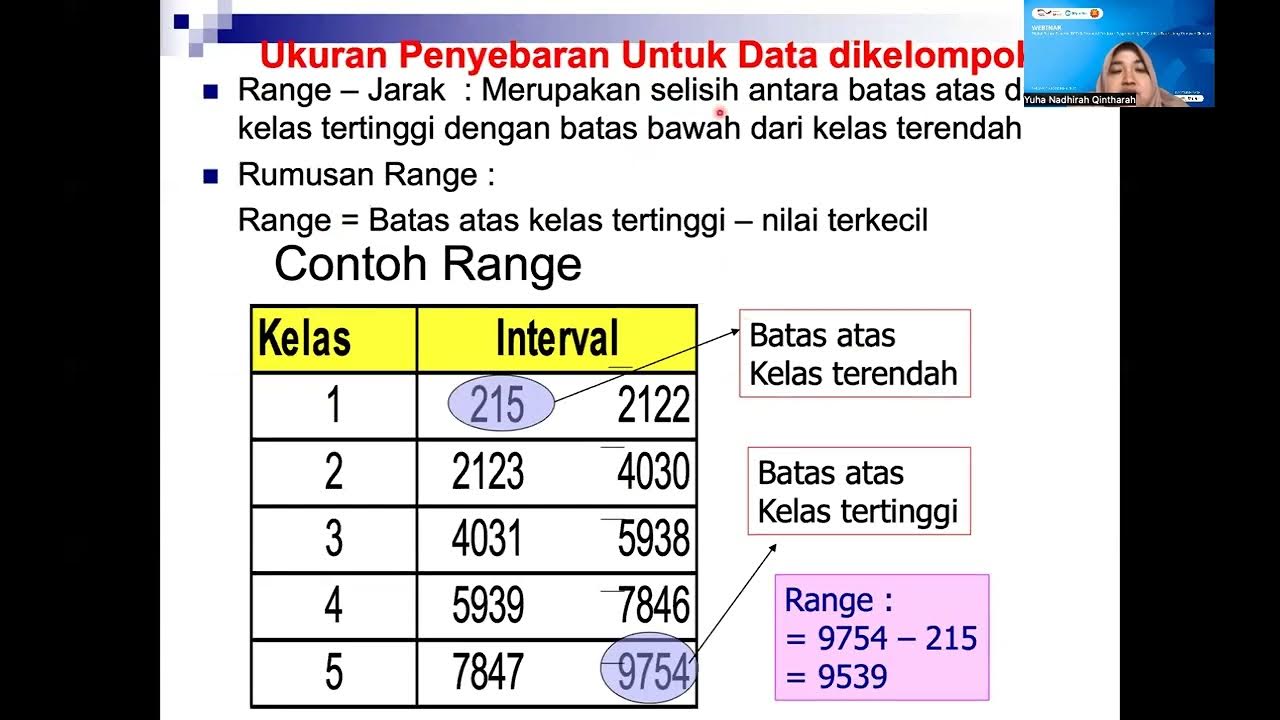
• 😀 The range is the difference between the highest and lowest values in a data set but doesn’t account for all values, making it less reliable for variability.
• 😀 To calculate the range, subtract the smallest value from the largest value in the data set.
• 😀 Variance measures the average squared deviation from the mean, with different formulas for population and sample data.
• 😀 Population variance is calculated as the sum of squared deviations divided by the total number of values, while sample variance divides by n - 1.
• 😀 Standard deviation is the square root of the variance, providing a more interpretable measure of data spread.
• 😀 For calculating standard deviation, first find the mean, then calculate the squared differences from the mean, sum them, divide by n (for population) or n - 1 (for sample), and finally take the square root.
• 😀 The standard deviation is a better measure of data spread compared to range because it considers all data points and is not affected by outliers.
• 😀 In an example of five values (2, 4, 7, 12, 15), the variance is 29.5, and the standard deviation is 5.43.
• 😀 In a practical application, standard deviation is used to determine which company's batteries are most consistent in performance, with smaller standard deviation indicating more consistent results.

Q & A

What is the main purpose of measures of variability or dispersion?

The main purpose of measures of variability or dispersion is to convey the idea of how spread out a data set is, offering insight into the consistency or variability of the data.

How is the range calculated?

The range is calculated by subtracting the smallest value from the largest value in the data set. It gives an idea of the spread but does not account for all values in the data set.

What is a limitation of using the range as a measure of dispersion?

A limitation of the range is that it only considers the largest and smallest values in the data set, meaning it does not account for outliers or the spread of all values within the data.

What is the formula for calculating the variance of a population?

The formula for calculating the variance of a population is σ² = Σ(x - μ)² / n, where x represents each data point, μ is the population mean, and n is the number of data points.

How do you calculate the variance for a sample data set?

To calculate the variance for a sample data set, the formula is s² = Σ(x - μ)² / (n - 1), where x represents each data point, μ is the sample mean, and n is the number of data points.

What is the standard deviation and how is it related to variance?

The standard deviation is a measure of how spread out numbers are in a data set. It is the square root of the variance, providing a more interpretable measure of dispersion in the same unit as the data.

What steps should be followed to calculate the standard deviation of a sample?

To calculate the standard deviation of a sample, first determine the mean, then calculate the deviation of each number from the mean. Square the deviations, sum them up, divide by n - 1, and take the square root of the result.

In the example with data set 2, 4, 7, 12, and 15, what is the mean?

The mean of the data set 2, 4, 7, 12, and 15 is 8, calculated by adding the values (2 + 4 + 7 + 12 + 15 = 40) and dividing by the number of data points (40 / 5 = 8).

In the provided example, what is the variance for the sample data set 2, 4, 7, 12, and 15?

The variance for the sample data set 2, 4, 7, 12, and 15 is 29.5, calculated by finding the squared differences from the mean, summing them, dividing by n - 1 (4), and obtaining the result.

Which company produced the most consistent batteries based on the standard deviation calculation?

Based on the standard deviation calculation, the company with the most consistent batteries is 'Dependable', as it has the smallest standard deviation of 0.72, indicating less variation in battery life expectancy.