Como hallar las componentes de un vector ↗️ | Ejemplo 2

Física en Acción

11 May 202007:44

Summary

TLDREl script del video ofrece una explicación detallada sobre cómo calcular las componentes rectangulares de un vector, utilizando como ejemplo un vector B que tiene una dirección hacia el suroeste y un ángulo de 32 grados con respecto a la horizontal. Seguidamente, se utiliza la trigonometría para hallar las componentes BX y BY, teniendo en cuenta las proyecciones asociadas a los ejes. Se enfatiza la importancia de la dirección y el sentido de las componentes, así como el uso adecuado de la calculadora en grados. El video también aporta consejos sobre cómo abordar los ángulos y las componentes desde una perspectiva física y matemática, y termina con una revisión de que las componentes no superen la magnitud del vector original, lo cual es una buena indicación de que el cálculo es correcto.

Takeaways

📚 Se discuten componentes de un vector en el contexto de física.
🔍 Se utiliza un ejemplo de un vector 'b' con dirección suroeste y un ángulo de 32 grados con respecto a la horizontal.
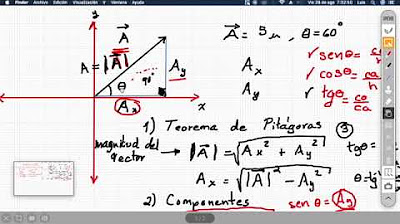
📐 Se identifica un triángulo rectángulo para resolver los componentes rectangulares 'bx' y 'by'.
📈 Se enfatiza la importancia de trabajar con las funciones trigonométricas y la configuración correcta de la calculadora en grados.
📉 Se explica cómo el componente 'bx' se calcula utilizando la función coseno, teniendo en cuenta la dirección del vector.
🔢 Se menciona que el coseno de 32 grados es aproximadamente -0.85, y se discute la importancia de los signos en las componentes.
🧭 Se destaca la diferencia entre la interpretación física y matemática de los ángulos y sus consecuencias en los signos de las componentes.
✅ Se sugiere verificar que las componentes calculadas no superen la magnitud del vector original como una forma de chequeo.
📝 Se describe el proceso para calcular la componente 'by' utilizando la función seno.
🔎 Se enfatiza la importancia de recordar las reglas de dirección para las componentes: negativo hacia la izquierda y abajo, positivo hacia la derecha y arriba.

Q & A

¿Qué es lo que se busca encontrar en el ejemplo dado en el guion?
-Se busca encontrar las componentes rectangulares bx y by de un vector b que tiene una dirección hacia el suroeste y un ángulo de 32 grados con respecto a la horizontal.
¿Cuál es la dirección del vector b mencionado en el guion?
-La dirección del vector b es hacia el suroeste.
¿Qué es lo que se considera al hallar las componentes rectangulares de un vector?
-Las componentes rectangulares son proyecciones asociadas a los ejes, donde se considera el ángulo que el vector forma con la horizontal y se utiliza trigonometría para calcular estas proyecciones.
¿Cómo se relaciona el ángulo de 32 grados con la horizontal para calcular las componentes del vector b?
-El ángulo de 32 grados se utiliza para determinar la posición del vector b en relación con la horizontal, permitiendo calcular las componentes bx y by utilizando funciones trigonométricas como el coseno y el seno.
¿Cuál es la función trigonométrica que se utiliza para calcular la componente bx del vector b?
-La función trigonométrica utilizada para calcular la componente bx es el coseno, donde bx = |b| * cos(32°).
¿Cómo se determina el signo de la componente bx del vector b?
-El signo de la componente bx se determina por la dirección del vector. Dado que la componente bx apunta hacia la izquierda (negativo en el marco de referencia del guion), el signo es negativo.
¿Cuál es el valor aproximado de la componente bx del vector b en kilómetros?
-El valor aproximado de la componente bx del vector b es de menos 51 kilómetros.
¿Qué función trigonométrica se utiliza para calcular la componente by del vector b?
-La función trigonométrica utilizada para calcular la componente by es el seno, donde by = |b| * sin(32°).
¿Cómo se determina el signo de la componente by del vector b?
-El signo de la componente by se determina por la dirección del vector. Dado que la componente by apunta hacia abajo (negativo en el marco de referencia del guion), el signo es negativo.
¿Cuál es el valor aproximado de la componente by del vector b en kilómetros?
-El valor aproximado de la componente by del vector b es de menos 30.18 kilómetros.
¿Por qué no pueden ser las componentes del vector b mayores que la magnitud del vector original?
-En los triángulos rectángulos, la hipotenusa es el lado de mayor longitud, por lo que las componentes (que son catetos) no pueden ser superiores a la magnitud del vector original.
¿Cómo se puede verificar si el ejercicio de hallar componentes de un vector está bien solucionado?
-Se puede verificar comparando las magnitudes de las componentes con la magnitud del vector original. Las componentes deben ser menores que la magnitud del vector para que el ejercicio sea correcto.