Componentes Rectangulares de un vector | Ejemplo 1

Matemáticas profe Alex

12 Feb 201914:09

Summary

TLDREn este video se explica cómo encontrar las componentes rectangulares de un vector. Se utiliza un ejemplo de un vector de 6 centímetros con una dirección de 30 grados norte. Se detalla la importancia de utilizar ángulos correctos y las razones trigonométricas para calcular las componentes x e y. Además, se ofrecen consejos para evitar errores comunes y se invita a practicar con ejercicios.

Takeaways

😀 El curso trata sobre vectores y cómo encontrar sus componentes rectangulares.
📚 Se explica detalladamente lo que son las componentes rectangulares de un vector.
📐 Se muestra cómo graficar un vector en un plano de coordenadas geográficas o puntos cardinales.
🧭 Se menciona que la dirección del vector es dada en grados norte y este es el primer video de la serie.
📏 Se describe el proceso de trazado de un vector y cómo se relaciona con los ángulos y las componentes rectangulares.
📈 Se utiliza trigonometría para encontrar las componentes rectangulares: seno para la componente y y coseno para la componente x.
🔢 Se da un ejemplo práctico de cómo calcular las componentes rectangulares de un vector que mide seis centímetros y tiene un ángulo de 30 grados.
💡 Se sugiere que es importante recordar que el ángulo siempre debe ser el que sale del este o del oeste.
📉 Se enfatiza la importancia de comprobar los resultados con un dibujo para asegurarse de que las componentes son correctas.
🎓 Se invita a los estudiantes a practicar con ejercicios y a ver más contenido del curso para profundizar en el tema.

Q & A

¿Qué es lo que se busca encontrar en el curso de vectores mencionado en el script?
-Se busca encontrar las componentes rectangulares de un vector, es decir, las componentes x e y de un vector en un plano cartesiano.
¿Cómo se describe el vector A en el script?
-El vector A se describe como un vector que mide seis centímetros y tiene una dirección dada por 30 grados norte.
¿Qué es lo que se sugiere hacer antes de encontrar las componentes rectangulares de un vector?
-Se sugiere graficar el vector en un plano de coordenadas geográficas o puntos cardinales para visualizar su dirección y magnitud antes de calcular sus componentes.
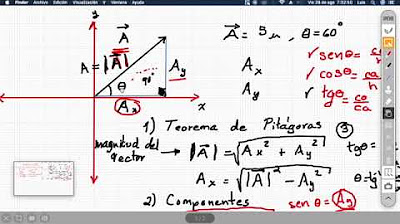
¿Cuál es la relación entre la magnitud de un vector y sus componentes rectangulares en un triángulo rectángulo?
-La magnitud del vector es igual a la hipotenusa del triángulo rectángulo formado por las componentes rectangulares del vector.
¿Cómo se relacionan las componentes rectangulares de un vector con las funciones trigonométricas?
-Las componentes rectangulares de un vector se relacionan con las funciones trigonométricas sen y cos, donde la componente y es igual a la magnitud del vector multiplicada por el seno del ángulo y la componente x es igual a la magnitud del vector multiplicada por el coseno del ángulo.
¿Qué es el ángulo que se debe utilizar para calcular las componentes rectangulares de un vector?
-El ángulo que se debe utilizar es el ángulo que sale del este o del oeste, y siempre debe ser el que forma un ángulo recto con el eje x o con el eje este-oeste.
¿Cómo se determina si la componente x de un vector es positiva o negativa?
-La componente x de un vector es positiva cuando el vector apunta hacia la derecha y negativa cuando apunta hacia la izquierda en un plano cartesiano.
¿Cómo se determina si la componente y de un vector es positiva o negativa?
-La componente y de un vector es positiva cuando el vector apunta hacia arriba (norte) y negativa cuando apunta hacia abajo (sur) en un plano cartesiano.
¿Qué es lo que se sugiere hacer para verificar la precisión de las componentes rectangulares calculadas?
-Se sugiere hacer un dibujo para comparar las componentes rectangulares calculadas con la representación gráfica del vector, asegurándose de que la componente x sea más larga que la componente y en el caso del vector A.
¿Qué consejos se dan para evitar errores al calcular las componentes rectangulares de un vector?
-Se sugiere tener cuidado con el ángulo utilizado, asegurándose de que sea el ángulo correcto que sale del este o del oeste, y también verificar que la componente x sea más larga que la componente y para los vectores que apunten hacia el este.

Outlines

00:00

📚 Introducción al curso de vectores y componentes rectangulares

El primer párrafo presenta el inicio de un curso sobre vectores, enfocado en encontrar las componentes rectangulares de un vector. Se describe un ejemplo práctico de un vector que mide seis centímetros y cuya dirección es de 30 grados norte. El instructor explica que, aunque no es necesario, traza el vector en un plano de coordenadas geográficas para ilustrar el concepto. La intención es que los estudiantes comprendan y no simplemente memoricen las fórmulas. Se menciona que las componentes rectangulares son dos líneas paralelas a los ejes, y se utiliza un triángulo rectángulo para explicar cómo se relacionan con la magnitud del vector y los ángulos.

05:00

📐 Explicación detallada de las fórmulas de componentes rectangulares

En el segundo párrafo, se profundiza en la explicación de cómo se calculan las componentes rectangulares de un vector utilizando trigonometría. Se introducen las fórmulas para encontrar la componente x (relacionada con el coseno del ángulo) y la componente y (relacionada con el seno del ángulo). El instructor enfatiza la importancia de utilizar el ángulo correcto, que debe ser el que sale del este o del oeste, y no el que sale del norte o del sur. Se da un ejemplo concreto de cómo se calcula la componente x y la componente y para un vector de seis centímetros a un ángulo de 30 grados, obteniendo resultados de 5.19 centímetros para la componente x y 3 centímetros para la componente y. Además, se aconseja a los estudiantes prestar atención a la dirección del vector para determinar si las componentes son positivas o negativas.

10:02

📘 Consejos y práctica para entender mejor las componentes rectangulares

El tercer párrafo ofrece consejos y prácticas para que los estudiantes mejoren su comprensión de las componentes rectangulares. Se sugiere que siempre se tenga en cuenta que el ángulo se refiere al que sale del este o del oeste y no del norte o del sur. Se da un ejemplo de cómo se podría confundir el ángulo al graficar y cómo se debe utilizar el ángulo correcto para calcular las componentes. Se calculan las componentes para un vector de doce centímetros a un ángulo de 50 grados, obteniendo resultados positivos para ambas componentes. El instructor recomienda comparar los resultados con un dibujo para verificar la precisión. Finalmente, se invita a los estudiantes a profundizar más en el tema mediante el curso completo o otros videos recomendados, y se les alienta a suscribirse, comentar, compartir y dar like al video.

Mindmap

Keywords

💡Vectores

Los vectores son objetos geométricos que tienen una dirección y una magnitud. En el video, se utiliza un vector para ilustrar cómo encontrar sus componentes rectangulares. El vector mencionado en el script tiene una magnitud de seis centímetros y una dirección de 30 grados norte, lo que es crucial para calcular sus componentes x e y.

💡Componentes rectangulares

Las componentes rectangulares de un vector son sus proyecciones sobre los ejes x e y en un sistema de coordenadas cartesiano. En el video, se busca encontrar estas componentes para el vector dado. Se menciona que la componente x se encuentra con la función coseno del ángulo y la componente y con la función seno del ángulo.

💡Magnitud del vector

La magnitud de un vector es su longitud o tamaño, que en el video es de seis centímetros. La magnitud es fundamental para calcular las componentes rectangulares, ya que estas se relacionan con ella a través de las funciones trigonométricas coseno y seno.

💡Ángulo

El ángulo es la medida en la que un vector se desvía de un eje de referencia, en este caso, el este. En el video, el ángulo de 30 grados norte es esencial para determinar las componentes rectangulares del vector. Se enfatiza la importancia de utilizar el ángulo correcto al realizar los cálculos trigonométricos.

💡Seno

El seno es una función trigonométrica que relaciona el cateto opuesto con la hipotenusa en un triángulo rectángulo. En el video, se utiliza el seno del ángulo para calcular la componente y del vector, siendo fundamental para la resolución del problema propuesto.

💡Coseno

El coseno es otra función trigonométrica que relaciona el cateto adyacente con la hipotenusa en un triángulo rectángulo. En el contexto del video, se utiliza el coseno del ángulo para calcular la componente x del vector, lo que es crucial para determinar su dirección en el plano cartesiano.

💡Triángulo rectángulo

Un triángulo rectángulo es un triángulo en el que un ángulo es de 90 grados. En el video, se forma un triángulo rectángulo con la magnitud del vector y sus componentes x e y, lo que permite aplicar las relaciones trigonométricas para calcular estas componentes.

💡Eje x

El eje x es uno de los ejes principales en un sistema de coordenadas cartesiano, generalmente asociado con la dirección horizontal. En el video, la componente x del vector se proyecta sobre el eje x, y se calcula utilizando la función coseno del ángulo.

💡Eje y

El eje y es el otro eje principal en un sistema de coordenadas cartesiano, asociado con la dirección vertical. En el video, la componente y del vector se proyecta sobre el eje y y se calcula utilizando la función seno del ángulo.

💡Gráfica

La gráfica es una representación visual de los datos, en este caso, del vector y sus componentes. Aunque en el video se menciona que no es obligatorio realizar la gráfica para encontrar las componentes, se utiliza para ilustrar y verificar los resultados obtenidos a través de las fórmulas trigonométricas.

Highlights

Bienvenida al curso de vectores y explicación de cómo encontrar las componentes rectangulares de un vector.

Se presentará un ejemplo práctico para encontrar las componentes rectangulares de un vector.

Se explicarán los conceptos básicos de las componentes rectangulares en un plano de coordenadas geográficas.

Se graficará rápidamente un vector para ilustrar cómo se relacionan con los puntos cardinales.

Se explicará la importancia de los ángulos y cómo se relacionan con las componentes rectangulares.

Se destacará que el ángulo siempre debe ser el que sale del este o del oeste.

Se explicará cómo se forman los triángulos rectángulos y cómo se relacionan con las componentes x e y de un vector.

Se presentará la fórmula para encontrar la componente y de un vector utilizando el seno del ángulo.

Se explicará cómo se utiliza la magnitud del vector y el ángulo para calcular la componente y.

Se presentará la fórmula para encontrar la componente x de un vector utilizando el coseno del ángulo.

Se destacará la importancia de la dirección del vector para determinar si las componentes son positivas o negativas.

Se explicará cómo se relacionan las direcciones norte, este, sur y oeste con las componentes x e y.

Se dará un ejemplo práctico de cómo calcular las componentes rectangulares de un vector de 6 centímetros y 30 grados norte.

Se explicará cómo se utiliza la calculadora para realizar los cálculos necesarios.

Se destacará la importancia de verificar los resultados con un dibujo para asegurar la precisión.

Se presentará un ejercicio para que los estudiantes practiquen los conceptos aprendidos.

Se ofrecerán consejos para evitar errores comunes al calcular las componentes rectangulares.

Se invitará a los estudiantes a suscribirse, comentar, compartir y dar like al video para profundizar en el tema.