Matematika Kelas 9 Bab 3 Transformasi Geometri - A. Translasi hal. 136 - 143 Kurikulum Merdeka
Summary
TLDRThis video explores the concept of translation in geometry, specifically how to shift geometric shapes on a Cartesian plane using translation components. It covers practical examples, such as translating a kite or a square, while emphasizing the congruency of shapes before and after the translation. The tutorial includes step-by-step demonstrations of how to apply translation to various geometric objects and lines, helping students grasp this fundamental transformation in geometry.
Takeaways
- 😀 The video focuses on teaching geometric transformations, specifically 'translation' (pergeseran) in mathematics for Grade 9 students.
- 😀 Translation is the process of shifting an object, such as a shape, from one position to another without changing its size or orientation.
- 😀 A real-life example of translation is shown by observing the movement of a chair being shifted by a student or a vehicle moving on the road.
- 😀 During an exploration activity, students are asked to trace and cut out a kite-shaped figure and then translate it on a grid by following a specific directional line.
- 😀 In the translation process, the original shape (kite ABCD) and the translated shape (kite EFGH) are congruent, meaning they have the same size and shape.
- 😀 The direction and distance of a translation can be represented by a directed line segment, such as from point A to point E.
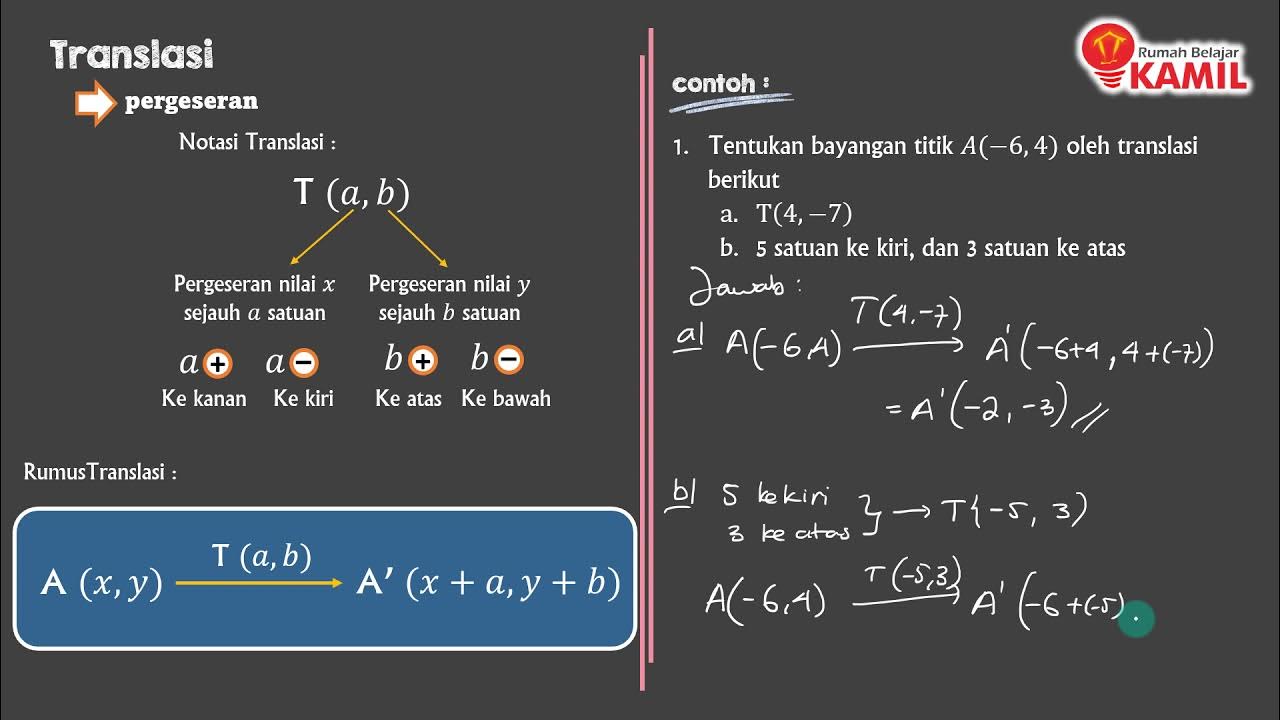
- 😀 Translations can be expressed using 'horizontal' (A) and 'vertical' (B) components, such as a translation of (4, 2) or (-4, -2).
- 😀 The coordinates of a translated point can be found using the formula: x' = x + A, y' = y + B, where (x, y) is the original point.
- 😀 The video also provides examples of translating shapes (such as squares and triangles) on a coordinate plane by shifting them by given components.
- 😀 A real-world application of translation is demonstrated with the translation of a straight line equation (e.g., 2x + 3y = 6) on a coordinate plane, using a translation component like (3, -4).
Q & A
What is translation in geometry?
-Translation, or 'pergeseran', in geometry is the movement of an object (such as a point, line, or shape) from one position to another, maintaining its size and shape but shifting it by a specific distance in a given direction.
What is the key property of a shape after a translation?
-After a translation, the shape retains its size, orientation, and angles. It is congruent to the original shape, meaning both have identical dimensions and shape but are located at different positions.
How can a translation be represented mathematically?
-A translation can be represented using components, often in the form of a pair of values (a, b). The value 'a' represents the horizontal shift (positive for right, negative for left), and 'b' represents the vertical shift (positive for up, negative for down).
What is the significance of the arrows shown in the translation example of the kite?
-The arrows in the translation example indicate the direction and magnitude of the shift. For instance, arrows showing the movement from points A to E, B to F, and so on, illustrate how each part of the shape shifts in a specific direction and distance.
What does 'kongruen' mean in the context of translation?
-'Kongruen' means that the translated shape is congruent to the original shape. This means that after translation, the shape's size, angles, and side lengths remain unchanged, just displaced to a new location.
In the example, how do the components (4, 2) in the translation relate to the movement of the points?
-In the translation example, the components (4, 2) indicate that every point of the object is moved 4 units to the right (horizontal shift) and 2 units up (vertical shift). This translation is reflected in the movement of the kite's vertices.
What is the formula for finding the translated coordinates of a point?
-The formula for finding the translated coordinates of a point (x, y) is: x' = x + a and y' = y + b, where 'a' and 'b' are the horizontal and vertical translation components, respectively.
What is the difference between the two shapes in the exploration example (the square and rhombus)?
-The difference lies in their shape. The square is a rectangle with equal sides and 90-degree angles, while the rhombus, despite having equal side lengths, has opposite angles that are not 90 degrees. The translation does not change the shape's inherent properties, but the transformed square into a rhombus indicates a different type of transformation, not purely a translation.
How do we determine if a transformation is a translation or something else?
-A transformation is considered a translation if the object maintains its shape, size, and orientation, but moves a constant distance in a particular direction. If the shape changes its orientation, size, or angles, it is a different type of transformation (e.g., rotation or dilation).
In the example of the translated triangle, what does the translation result in?
-In the example of the translated triangle, the result is a new triangle that is congruent to the original one. The translated triangle's vertices shift according to the specified components, and the shape remains the same but is moved to a new position on the coordinate plane.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Transformasi Geometri [Part 2] - Translasi (Pergeseran)
Matematika Kelas 9 : Transformasi Geometri (part 1 : Translasi)

TRANSFORMASI GEOMETRI | TRANSLASI

TRANSFORMASI FUNGSI PART 2 (TRANSLASI FUNGSI)

MATEMATIKA KELAS 9 HALAMAN 137-143 KURIKULUM MERDEKA EDISI 2022

TRANSLASI (PERGESERAN) || TRANSFORMASI GEOMETRI
5.0 / 5 (0 votes)
