TRANSFORMASI FUNGSI PART 2 (TRANSLASI FUNGSI)
Summary
TLDRThis video tutorial focuses on the concept of function transformations, specifically translation in geometry. It explains how to apply translations represented by matrices to shift objects in 2D space along the x and y axes. The instructor provides step-by-step examples, including moving points and lines, and illustrates the process with Cartesian coordinates. The lesson also covers how to transform the equation of a line when it undergoes translation, using matrix operations to find the new equation of the translated line.
Takeaways
- 📚 The lesson is about learning function transformations, focusing on three main types: translation (shifting), reflection (mirroring), and dilation (scaling up or down).
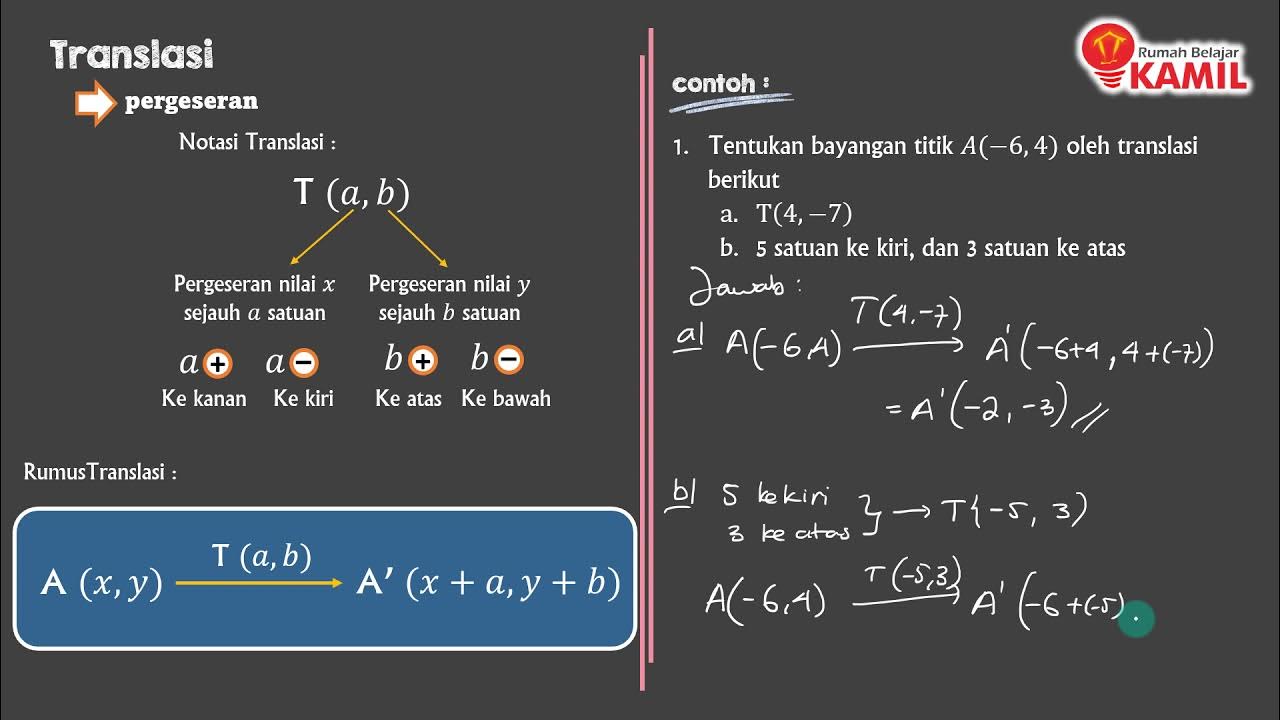
- 🔍 Translation in geometry involves moving an object in 2D space in a certain direction, represented by a matrix with elements 'a' for horizontal shift and 'b' for vertical shift.
- 👉 'a' indicates the horizontal shift along the x-axis; a positive value means a shift to the right, while a negative value means a shift to the left.
- 📏 'b' represents the vertical shift along the y-axis; a positive value indicates an upward shift, while a negative value indicates a downward shift.
- 📈 The concept of translation is illustrated with examples using a Cartesian coordinate system, showing how points are shifted based on the values of 'a' and 'b'.
- 🔢 An example of a translation is given as (-4, 3), meaning a shift of 4 units to the left and 3 units up.
- 📉 Another example is (0, -2), indicating no horizontal shift and a shift of 2 units down.
- 🔄 The script also covers the transformation of a line with the equation 2x - 3y + 5 = 0, demonstrating how it is translated by the values 'a' and 'b'.
- 📐 The transformation of the line equation is explained step by step, showing how to adjust the equation to represent the new position after translation.
- 📈 The final equation of the translated line is given as 3x - 2y - 7 = 0, resulting from a translation of 2 units to the right and 3 units down.
- 🖌️ The script concludes with a visual representation using an application like Geogebra to illustrate the original and translated lines.
- 📝 The lesson ends with exercises for students to practice translating points and lines, with specific examples provided for them to work through.
Q & A
What is the main topic of the video lesson?
-The main topic of the video lesson is the transformation of functions, specifically focusing on the three most commonly used transformations: translation, reflection, and dilation.
What are the three types of transformations discussed in the video?
-The three types of transformations discussed are translation (or shifting), reflection (or mirroring), and dilation (or stretching and compressing).
What is a translation in the context of geometry?
-In geometry, a translation is the process of moving an object in a 2D plane in a certain direction by a specified distance, which can be represented by a matrix.
How is the direction and distance of a translation represented in the video?
-The direction and distance of a translation are represented by a matrix with two values, 'a' for horizontal movement along the x-axis and 'b' for vertical movement along the y-axis.
What does the value of 'a' in a translation matrix indicate?
-The value of 'a' in a translation matrix indicates the horizontal movement of an object. A positive value means the object moves to the right, while a negative value means it moves to the left.
What does the value of 'b' in a translation matrix indicate?
-The value of 'b' in a translation matrix indicates the vertical movement of an object. A positive value means the object moves upwards, while a negative value means it moves downwards.
Can you provide an example of a translation transformation discussed in the video?
-An example of a translation transformation discussed in the video is moving an object by 4 units to the left and 3 units upwards, represented by the matrix [-4, 3].
How is the transformation of a function represented in the video?
-The transformation of a function is represented by applying the translation matrix to the function's equation, resulting in a new equation that represents the transformed function.
What is the result of translating the line with the equation 3x - 2y + 5 = 0 by 2 units to the right and 3 units down?
-The result of translating the line with the equation 3x - 2y + 5 = 0 by 2 units to the right and 3 units down is a new line with the equation 3x - 2y - 7 = 0.
How can the transformed equation of a function be derived from the original equation using a translation matrix?
-The transformed equation of a function can be derived by substituting the original variables (x and y) with the new variables (x' and y') obtained from the translation matrix, and then simplifying the resulting equation.
What is the significance of understanding the transformations of functions in mathematics?
-Understanding the transformations of functions in mathematics is significant as it helps in visualizing and manipulating geometric shapes, solving complex problems, and provides a deeper comprehension of the behavior of functions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Materi Lengkap Translasi (Pergeseran) || TRANSFORMASI GEOMETRI

Matematika Kelas 9 Bab 3 Transformasi Geometri - A. Translasi hal. 136 - 143 Kurikulum Merdeka

TRANSLASI (PERGESERAN) || TRANSFORMASI GEOMETRI

Transformasi gabungan
Matematika Kelas 9 : Transformasi Geometri (part 1 : Translasi)

MATEMATIKA KELAS 9 HALAMAN 137-143 KURIKULUM MERDEKA EDISI 2022
5.0 / 5 (0 votes)