Video Pembelajaran Matematika Materi Trigonometri Kelas 10 - Nilai Trigonometri pada Sudut Istimewa
Summary
TLDRThis educational video explains the basic trigonometric ratios—sine, cosine, and tangent—using right-angled triangles and the unit circle. It covers the key properties of special angles (0°, 30°, 45°, 60°, and 90°), demonstrating how to calculate trigonometric values for each. The video also addresses common questions, such as the role of reference angles and the effects of using different angles as references. Through clear explanations and visual aids, viewers learn how to easily determine trigonometric ratios, which are essential for solving problems in mathematics and physics.
Takeaways
- 😀 Trigonometric ratios such as sine (sin), cosine (cos), and tangent (tan) are foundational concepts in trigonometry, used to describe the relationships between the angles and sides of a right triangle.
- 😀 The sine, cosine, and tangent ratios can be remembered using simple mnemonics such as 'Sindemi' for sine, 'Kosami' for cosine, and 'Tandesa' for tangent.
- 😀 The choice of reference angle in a triangle is important, and different angles can be used as the base for calculating the trigonometric ratios, with proper attention to the sides labeled as 'front', 'side', and 'hypotenuse'.
- 😀 Special angles such as 0°, 30°, 45°, 60°, and 90° have unique properties in trigonometry, which make calculating their trigonometric ratios easier and more systematic.
- 😀 For a 30°-60°-90° triangle, the ratio of the sides is 1:√3:2, and the trigonometric ratios for sin(30°), cos(30°), and tan(30°) can be derived directly from this relation.
- 😀 In the 30°-60°-90° triangle, sin(30°) = 1/2, cos(30°) = √3/2, and tan(30°) = 1/√3 (which simplifies to √3/3).
- 😀 In a 45°-45°-90° triangle (isosceles right triangle), both legs are of equal length, and the hypotenuse is √2 times the length of a leg, leading to the ratios sin(45°) = cos(45°) = 1/√2.
- 😀 The value of sin(45°) and cos(45°) simplifies to 1/√2, which can be rationalized to √2/2.
- 😀 The unit circle is a helpful tool for visualizing trigonometric ratios. It is a circle with a radius of 1, and its relationships help in deriving values for trigonometric functions at specific angles like 0°, 30°, 45°, 60°, and 90°.
- 😀 At an angle of 0°, sin(0°) = 0, cos(0°) = 1, and tan(0°) = 0, showing how the length of the triangle's 'front' side shrinks as the angle approaches 0°.
- 😀 At 90°, the length of the 'side' shrinks to 0, and the ratio for sin(90°) becomes 1, while cos(90°) becomes 0, and tan(90°) is undefined (since it involves division by 0).
Q & A
What are the trigonometric ratios discussed in the video?
-The trigonometric ratios discussed in the video are sine (sin), cosine (cos), and tangent (tan). These ratios are derived from the sides of a right-angled triangle.
How do you calculate the sine of an angle?
-The sine of an angle is calculated by dividing the length of the side opposite the angle (Sisi depan) by the length of the hypotenuse (Sisi miring).
What does the video say about using different reference angles?
-The video explains that you can use any angle as the reference angle in a right triangle, but the assignment of sides (opposite, adjacent, and hypotenuse) will change based on the chosen angle.
Can the right angle (90°) be used as a reference angle?
-While you can theoretically use a 90° angle, the video explains that using it would cause the triangle to degenerate (sides become coincident) and lead to undefined values for certain trigonometric functions like tan 90°.
What is special about the 30°-60°-90° triangle?
-In a 30°-60°-90° triangle, the side opposite the 30° angle is half the length of the hypotenuse. This property allows for simple calculation of the trigonometric ratios.
What is the relationship between the sides in a 45°-45°-90° triangle?
-In a 45°-45°-90° triangle, the two legs are equal in length, and the hypotenuse is √2 times the length of one leg.
How do you calculate the tangent of 30°?
-The tangent of 30° is calculated as the ratio of the side opposite 30° (Sisi depan) to the side adjacent to 30° (Sisi samping), which results in 1/√3 or 1/3√3 when rationalized.
What is the significance of the unit circle in trigonometry?
-The unit circle is used to find the trigonometric values for angles like 0° and 90°. It helps visualize how the lengths of the sides of a triangle change as the angle increases or decreases.
What happens to the side lengths in a unit circle as the angle approaches 90°?
-As the angle approaches 90°, the side adjacent to the angle (Sisi samping) approaches zero, while the side opposite the angle (Sisi depan) and the hypotenuse (Sisi miring) become equal in length.
Why is Tan 90° considered undefined?
-Tan 90° is undefined because, in the unit circle, the adjacent side (Sisi samping) becomes zero, and division by zero is not defined in mathematics.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
¿Qué son las razones trigonométricas? @MatematicasprofeAlex

Matematika SMA - Trigonometri (1) - Pengenalan Trigonometri, Perbandingan Trigonometri (A)

Menentukan Nilai Trigonometri Segitiga Siku Siku Perbandingan Trigonometri segitiga Siku Siku

TRIGONOMETRI - Ukuran Sudut dan Perbandingan Trigonometri

Contoh Soal Perbandingan Trigonometri pada segitiga siku siku
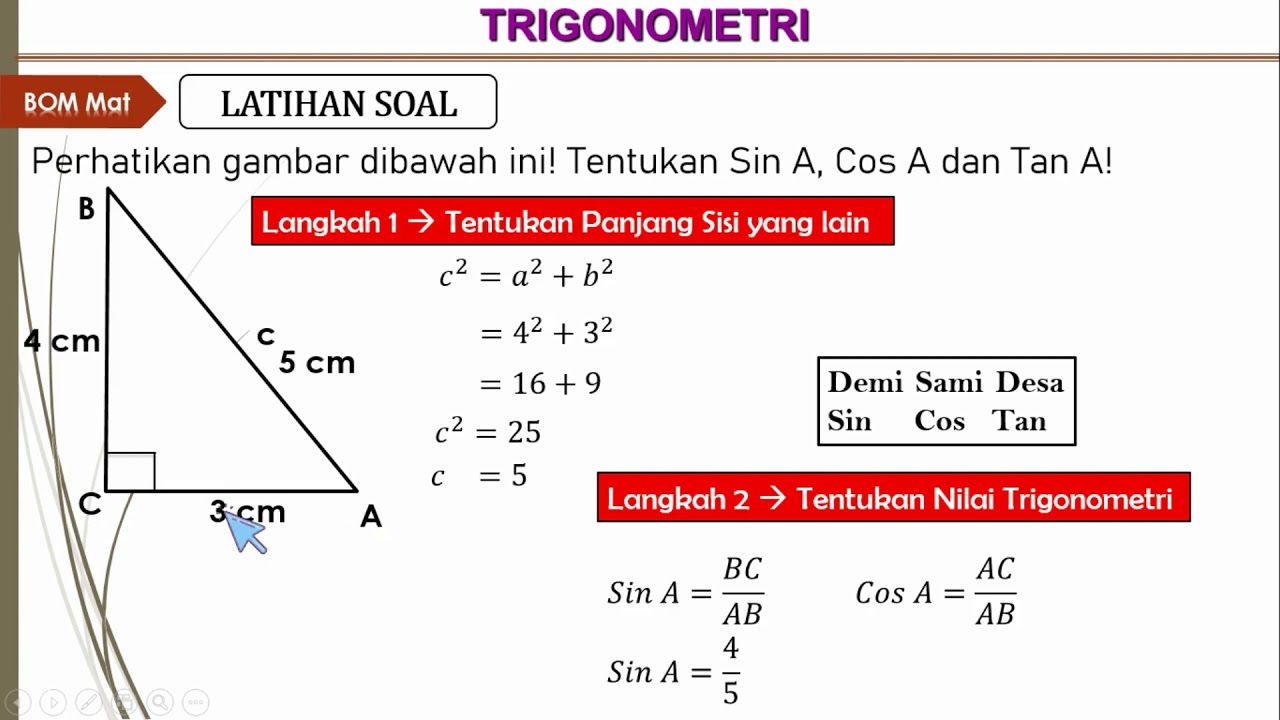
Perbandingan trigonometri pada segitiga siku siku, Menjelaskan rasio trigonometri
5.0 / 5 (0 votes)
