Kalkulus 1: Fungsi dan Grafik Fungsi
Summary
TLDR本视频介绍了函数的基本概念及其图形表示。讲解了函数的定义、域与值域的关系、以及如何通过示例区分是否为函数。通过两个集合 A 和 B 的示例,阐述了每个元素在域 A 中都必须与集合 B 中的唯一元素配对。接着,讲解了如何通过图形展示函数,并提供了具体的图形例子,如 y = x + 1 和 y = x^2,帮助理解函数与图形的关系。最后,强调了点的数量与图形清晰度之间的关系,以及如何根据不同的点绘制函数图形。
Takeaways
- 😀 函数是一个规则,将一个集合(定义域)中的每个元素与另一个集合(值域)中的一个元素配对。
- 😀 为了使关系成为函数,定义域中的每个元素必须与值域中的一个唯一元素对应。
- 😀 第一个函数条件:每个定义域中的元素都必须与值域中的一个元素配对。
- 😀 第二个函数条件:定义域中的每个元素都必须与值域中的一个且仅一个元素配对。
- 😀 在函数定义中,定义域(A集合)和值域(B集合)通过函数f连接,每个A中的元素都有一个唯一的B中元素配对。
- 😀 函数的定义要求定义域中的每个元素只能有一个配对,不能有多个配对。
- 😀 例子展示了一个满足条件的函数,其中定义域A的每个元素都对应值域B中的一个元素。
- 😀 如果定义域A中的一个元素有多个配对,或者定义域A中的元素没有完全配对,这就不是一个函数。
- 😀 函数的图像是由一组点(X, Y)组成,其中每个X值(定义域的元素)与一个Y值(值域的元素)配对。
- 😀 通过代入x值(例如x=1, 2, 3等)来计算对应的y值,并绘制函数图像,可以更好地理解函数的关系和形态。
Q & A
什么是函数的定义?
-函数是一个规则或对应关系,它将每个定义域中的元素映射到唯一的值,这个值属于值域。
什么是定义域和值域?
-定义域是函数中输入值的集合,值域是输出值的集合。函数将定义域中的每个元素映射到值域中的一个元素。
函数的两个主要条件是什么?
-第一个条件是每个定义域中的元素都必须映射到值域中的唯一元素;第二个条件是定义域中的每个元素必须被映射到值域中的某个元素,且定义域的所有元素都必须被映射。
给定的例子中,为什么A是一个有效的函数?
-因为每个定义域中的元素都对应着值域中的唯一元素,并且定义域的所有元素都被映射到值域中的元素。
为什么某些例子不是函数?
-因为在某些例子中,定义域中的元素有多个值与之对应,或者并非定义域中的所有元素都被映射到值域中的元素。
什么是函数图像?
-函数的图像是由满足函数方程的所有点(x, y)组成的集合,其中x是定义域中的元素,y是值域中的元素。
如何绘制函数 y = x + 1 的图像?
-首先,选择一些x值(如1, 2, 3等),然后将它们代入y = x + 1的方程中,得到对应的y值,再根据这些点绘制图像。
为什么增加更多的x值会使函数图像更精确?
-通过增加更多的x值,可以得到更多的坐标点,这样绘制的函数图像会更加平滑和精确,准确地反映函数的特性。
为什么y = x^2的图像是一个抛物线?
-因为在y = x^2的方程中,当x的值变化时,y值是x的平方,这种关系产生了一个对称的抛物线形状。
函数y = x^2图像中的对称性是什么?
-y = x^2的图像是关于y轴对称的,因为对于每一个正值x,都有对应的负值x,其y值相同,这使得图像呈现出对称性。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

What Is Entity Relationship Diagram ( ERD ) | ER Model Explained In DBMS With Examples

Intro to the Laplace Transform & Three Examples

Teorema fundamental del cálculo: definición y ejemplos
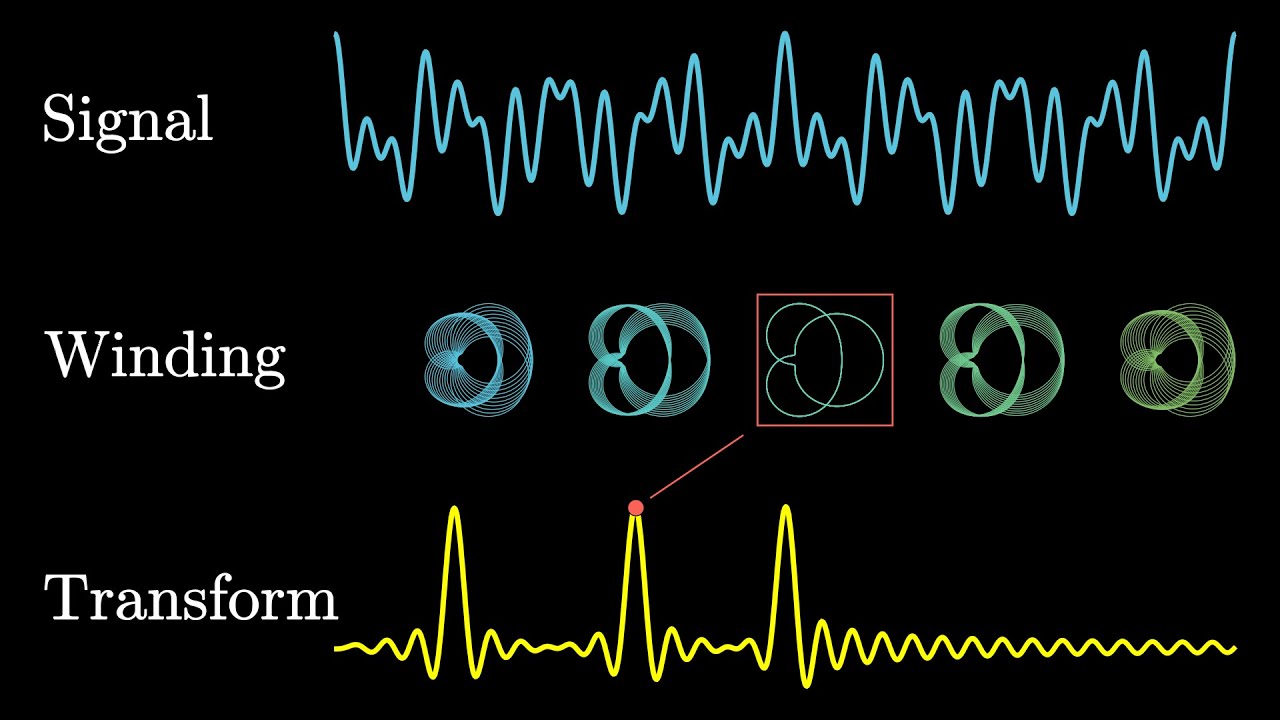
But what is the Fourier Transform? A visual introduction.

Hibridación del carbono

0625 Distribución geométrica

Hash table hash function
5.0 / 5 (0 votes)