Cuartiles, deciles y percentiles a partir de tablas con intervalos
Summary
TLDREn este video se explica cómo calcular las medidas de posición (cuartiles, deciles y percentiles) a partir de tablas de frecuencia con intervalos. A través de ejemplos prácticos, el video detalla los pasos para calcular el cuartil 1, el decil 3 y el percentil 78, utilizando las fórmulas correspondientes y el análisis de frecuencias acumuladas. Además, se enseña cómo interpretar los resultados para comprender mejor la distribución de los datos en una población, facilitando el análisis estadístico para los estudiantes y profesionales interesados en el tema.
Takeaways
- 😀 Las medidas de posición dividen los datos en m partes iguales, siendo los cuartiles, desiles y percentiles las más comunes.
- 😀 Los cuartiles dividen los datos en 4 partes iguales, los desiles en 10, y los percentiles en 100.
- 😀 El cálculo de estas medidas implica el uso de la fórmula K * n / m, donde K es el número de la medida de posición y m es el número de partes en las que se divide la distribución.
- 😀 Para el cuartil 1, se usa K=1; para el decil 3, K=3; y para el percentil 78, K=78.
- 😀 La fórmula K * n / m permite obtener un número que se compara con las frecuencias acumuladas para determinar la ubicación de la medida de posición en la tabla.
- 😀 En caso de que el valor obtenido de K * n / m no coincida exactamente con una frecuencia acumulada, se ubica entre dos valores: la frecuencia anterior (fi-1) y la frecuencia posterior (fi).
- 😀 Para calcular el cuartil 1, el decil 3 y el percentil 78, se deben identificar las frecuencias acumuladas que están cerca de los valores obtenidos de K * n / m.
- 😀 En cada caso, el intervalo que corresponde a la frecuencia posterior más alta se usa para determinar el límite inferior (Li) y la amplitud del intervalo.
- 😀 Para calcular el cuartil 1, el valor obtenido es 118.2, lo que indica que el 25% de los vendedores lograron una venta menor a este monto.
- 😀 El cálculo del percentil 78 da como resultado 166.25, lo que significa que el 78% de los vendedores tuvieron ventas menores o iguales a este valor.
- 😀 Las medidas de posición como cuartiles, desiles y percentiles son útiles para analizar y comprender la distribución de los datos, dividiéndolos en partes más pequeñas para su interpretación.
Q & A
¿Qué son las medidas de posición en estadística?
-Las medidas de posición son estadísticas que dividen un conjunto de datos en partes iguales. Las principales medidas de posición son los cuartiles, los desiles y los percentiles, que dividen los datos en 4, 10 y 100 partes iguales, respectivamente.
¿Cuáles son las diferencias entre cuartiles, desiles y percentiles?
-Los cuartiles dividen los datos en 4 partes iguales, los desiles en 10 partes iguales y los percentiles en 100 partes iguales. Estas divisiones nos permiten analizar la distribución de los datos de manera más detallada.
¿Qué es el factor K * n / m en el cálculo de las medidas de posición?
-El factor K * n / m se utiliza para determinar la posición de un valor dentro de un conjunto de datos agrupados. 'K' es el número de la medida de posición que se desea calcular, 'n' es el número total de datos y 'm' es el número de partes en las cuales se divide el conjunto de datos.
¿Cómo se calcula el cuartil 1 a partir de los datos?
-Para calcular el cuartil 1, se utiliza la fórmula K * n / m, donde K es 1, n es el número total de datos (500 en este caso) y m es 4. Luego, se busca en la tabla de frecuencias acumuladas el intervalo que contiene el valor obtenido y se calcula el cuartil utilizando la fórmula de interpolación.
¿Qué significa que el cuartil 1 sea 118.2 en este ejemplo?
-Significa que el 25% de los 500 vendedores lograron una venta menor a 118.2 dólares en su último día de trabajo. El cuartil 1 divide el conjunto de datos de tal manera que el 25% de los datos están por debajo de este valor.
¿Cómo se calcula el decil 3 en este caso?
-Para calcular el decil 3, se sigue el mismo proceso que para el cuartil, pero con K igual a 3 y m igual a 10. Luego, se utiliza la fórmula K * n / m para obtener la posición y se interpola entre las frecuencias acumuladas correspondientes al intervalo adecuado.
¿Qué interpretación tiene el decil 3 en este contexto?
-El decil 3 divide el conjunto de datos en 10 partes iguales. En este caso, el 30% de los 500 vendedores lograron una venta menor a 128.6 dólares en su último día de trabajo. El decil 3 muestra el valor que corresponde al 30% inferior de los datos.
¿Cómo se calcula el percentil 78?
-Para calcular el percentil 78, se usa la fórmula K * n / m, donde K es 78 y m es 100. El resultado nos da la posición en la tabla de frecuencias acumuladas, y luego se interpola entre los valores de frecuencia anterior y posterior del intervalo correspondiente.
¿Qué significado tiene el percentil 78 siendo 166.25?
-El percentil 78 indica que el 78% de los 500 vendedores lograron ventas menores o iguales a 166.25 dólares en su último día de trabajo. Los percentiles permiten comprender mejor cómo se distribuyen los datos en relación con el total.
¿Cómo se determina el intervalo adecuado para la interpolación de medidas de posición?
-El intervalo adecuado para la interpolación se determina observando la frecuencia acumulada correspondiente. Se busca el intervalo que contiene el valor K * n / m y se realiza la interpolación utilizando el límite inferior del intervalo y su amplitud.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
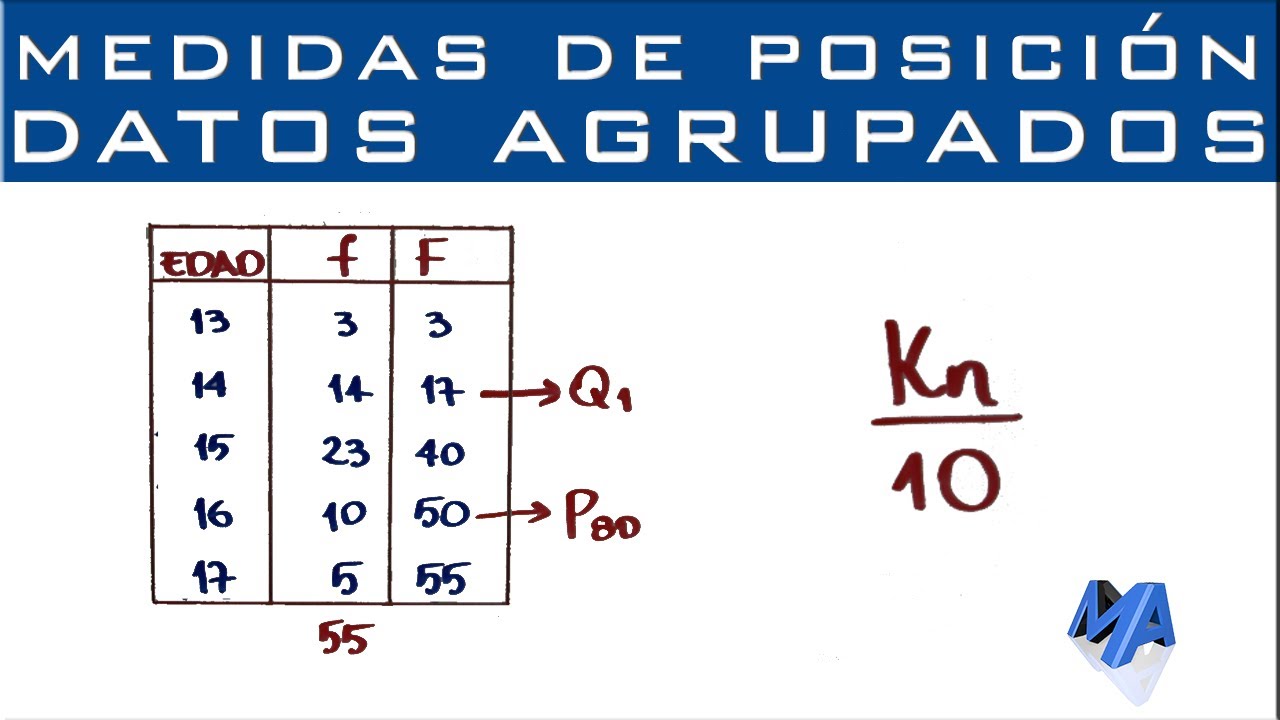
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS
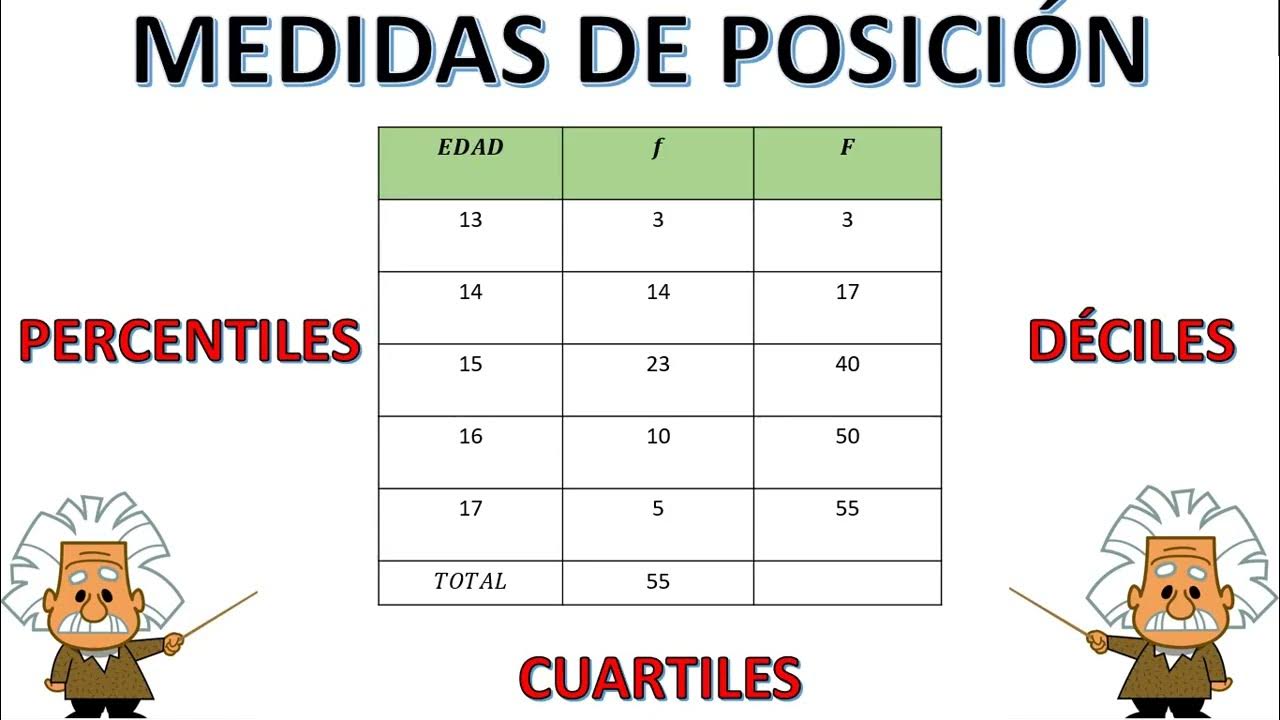
MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles
Parámetros de posición: mediana, cuartiles, deciles y percentiles, estadística descriptiva

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
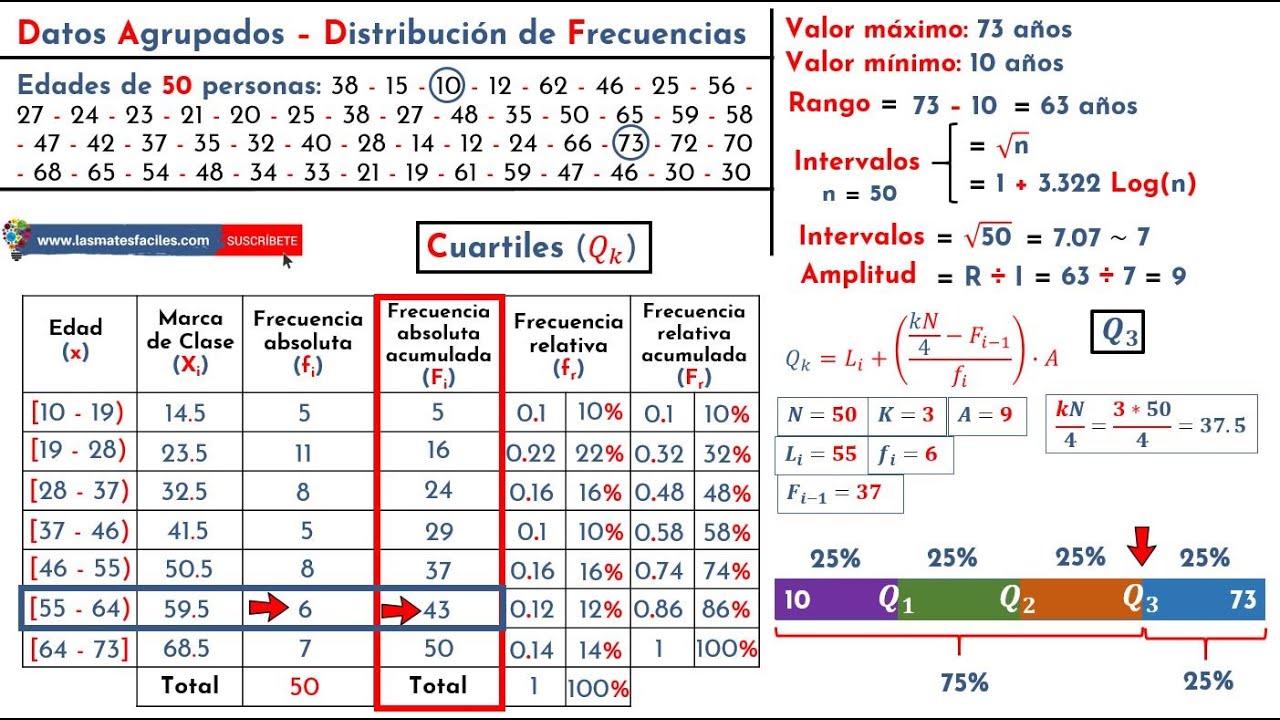
Cuartiles, Deciles y Percentiles - Datos Agrupados
5.0 / 5 (0 votes)
