MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles
Summary
TLDREn este video, se explica cómo calcular y entender las medidas de dispersión, como percentiles, deciles y cuartiles, utilizando una tabla de frecuencias. A través de ejemplos prácticos con la edad de estudiantes de diferentes grados, se muestra el proceso para hallar la frecuencia acumulada, las posiciones y cómo interpretar estos valores en contextos como el 5% o el 75% de los datos. También se enseña a utilizar fórmulas para calcular estos percentiles, deciles y cuartiles, ayudando a los estudiantes a comprender mejor cómo se distribuyen los datos y cómo hacer inferencias estadísticas. Ideal para aprender conceptos clave de estadística de manera clara y sencilla.
Takeaways
- 😀 Se explica cómo calcular los percentiles, deciles y cuartiles a partir de una tabla de frecuencias acumuladas.
- 😀 Se utiliza una tabla de edades de estudiantes de dos cursos para ejemplificar cómo trabajar con variables discretas.
- 😀 Para calcular los percentiles, se usa la fórmula K * n / 100, donde K es el percentil y n es el total de los datos.
- 😀 El percentil 5 se calculó y resultó en 13 años, lo que indica que el 5% de los datos tienen esa edad o menos.
- 😀 En el cálculo del percentil 75, la posición obtenida fue 41,25, lo que llevó a una edad de 16 años, reflejando que el 75% de los datos tienen 16 años o menos.
- 😀 Los deciles dividen el 100% en 10 partes iguales. El decil 3, por ejemplo, representó el 30% de los datos, y se encontró que equivalía a 14 años.
- 😀 Se mostró cómo los deciles también pueden ser calculados usando la fórmula K * n / 10, con K representando el decil.
- 😀 El cálculo del decil 9 dio como resultado 16 años, mostrando que el 90% de los datos tienen esa edad o menos.
- 😀 Los cuartiles dividen los datos en cuatro partes. El cuartil 2 es igual a la mediana, que representa el 50% de los datos.
- 😀 En el cálculo del cuartil 2 (la mediana), se encontró que el 50% de los estudiantes tienen 15 años o menos, lo que también reflejó la mayor frecuencia en los datos.
- 😀 Finalmente, se explicó que el cuartil 3 equivale al percentil 75, y se encontró que el 75% de los datos tiene 16 años o menos.
Q & A
¿Qué es una variable discreta?
-Una variable discreta es aquella que toma valores enteros, como en el caso de la edad de los estudiantes en este ejemplo.
¿Cómo se calcula la frecuencia acumulada?
-La frecuencia acumulada se calcula sumando las frecuencias absolutas de cada clase en orden secuencial. En el caso del ejemplo, se empieza con 3 estudiantes que tienen 13 años, luego se suma la frecuencia de 14 años, y así sucesivamente.
¿Qué son los percentiles?
-Los percentiles dividen el 100% de los datos en 100 partes iguales, representando cada uno un porcentaje específico de los datos.
¿Cómo se calcula un percentil?
-Para calcular un percentil, se utiliza la fórmula K * n / 100, donde K es el percentil deseado y n es el total de datos. La posición obtenida nos da el valor en el conjunto de datos correspondiente al percentil.
Si el resultado de la fórmula de percentiles no es un número entero, ¿qué se debe hacer?
-Si el resultado no es un número entero, se toma el siguiente número entero más cercano en la tabla de frecuencia acumulada.
¿Qué significa el percentil 5 en este ejemplo?
-El percentil 5 en este ejemplo corresponde a la edad de 13 años, lo que significa que el 5% de los estudiantes tienen 13 años o menos.
¿Qué son los deciles?
-Los deciles dividen el 100% de los datos en 10 partes iguales. Cada decil representa un 10% del total de los datos.
¿Cómo se calcula un decil?
-Para calcular un decil, se utiliza una fórmula similar a la de los percentiles, pero el divisor es 10. Por ejemplo, para hallar el tercer decil, se multiplica 3 * n (donde n es el total de datos) y luego se divide entre 10.
¿Qué es un cuartil?
-Los cuartiles dividen el conjunto de datos en cuatro partes iguales. El primer cuartil corresponde al 25% de los datos, el segundo cuartil es la mediana (50%), y el tercer cuartil corresponde al 75% de los datos.
¿Qué nos indica el cuartil 2 en este ejemplo?
-El cuartil 2, que es el 50% de los datos, corresponde a la mediana. En este caso, la mediana es 15 años, lo que significa que el 50% de los estudiantes tienen 15 años o menos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
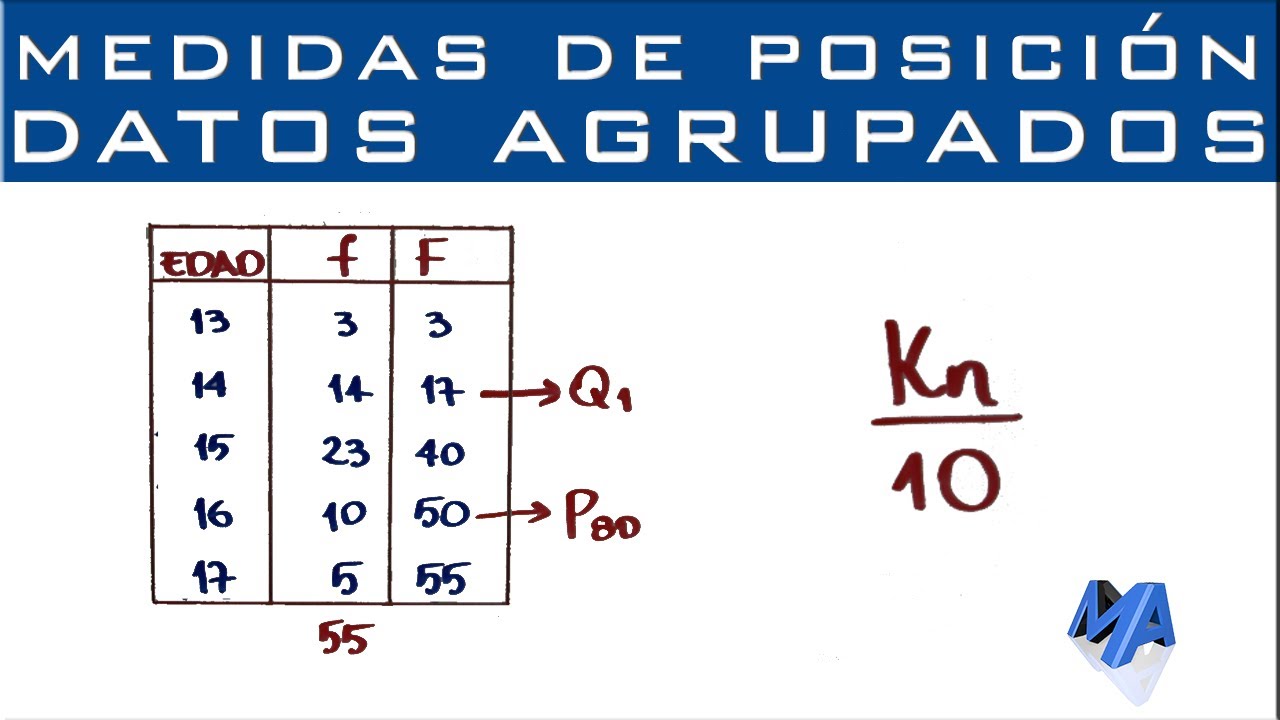
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS
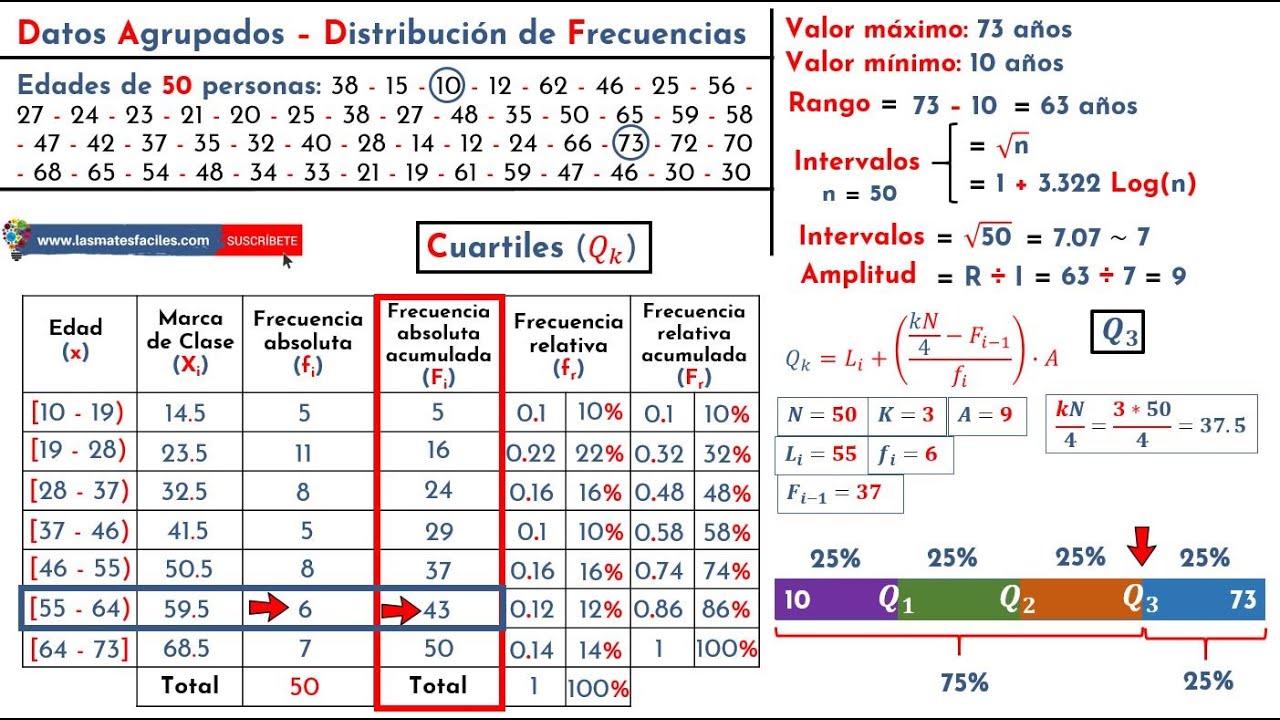
Cuartiles, Deciles y Percentiles - Datos Agrupados

Cuartiles, deciles y percentiles a partir de tablas con intervalos
Parámetros de posición: mediana, cuartiles, deciles y percentiles, estadística descriptiva

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
5.0 / 5 (0 votes)
