Karnaugh Map (K' Map) - Part 1
Summary
TLDRThis presentation introduces the Karnaugh map (K-map), a fundamental tool for logic minimization in digital circuits. It aims to clarify the concept for both beginners and those already familiar with K-maps but seeking a deeper understanding of their workings. The speaker explains the simplicity of using K-maps for simplifying Boolean expressions and emphasizes the importance of grasping the underlying logic to improve proficiency in solving complex problems. The session is ideal for anyone looking to enhance their knowledge of logic minimization techniques.
Takeaways
- 😀 K-map is an abbreviation for Karnaugh map, used in logic minimization.
- 😀 The presentation is aimed at people with different levels of understanding of K-maps.
- 😀 If you already know how to solve a K-map but don’t understand the underlying process, this lecture will clarify it.
- 😀 For those who are completely new to K-maps, this presentation offers an easy-to-understand introduction.
- 😀 K-maps are a useful tool for simplifying Boolean algebra expressions.
- 😀 The goal of the K-map is to minimize logic functions in a way that is both effective and efficient.
- 😀 Understanding how K-maps work is essential for simplifying complex logical expressions.
- 😀 The presentation encourages viewers to stay until the end for a full understanding of K-map applications.
- 😀 K-map is a visual method for minimizing logic functions by grouping adjacent cells that have 1s or 0s.
- 😀 This method helps in designing simpler, faster, and more efficient digital circuits.
- 😀 The speaker intends to explain the K-map from both a practical and theoretical perspective, covering both how and why it works.
Q & A
What is a K-map, and why is it important in logic minimization?
-A K-map, or Karnaugh map, is a diagrammatic method used to simplify Boolean algebra expressions. It allows the visualization of truth tables and helps in reducing logical expressions by grouping adjacent 1's in the map, making the overall logic simpler and more efficient.
Who would benefit from this K-map presentation?
-This presentation is designed for a wide audience, including people who already know about K-maps, those who are unfamiliar with K-maps but want to learn, and individuals who understand how to solve K-maps but want to understand the underlying principles.
What is the main goal of this presentation?
-The main goal is to introduce the K-map in a simple and understandable way, focusing not only on how to solve K-maps but also on explaining the underlying concepts to ensure a deeper understanding of how K-maps work.
Why should viewers watch the entire lecture if they already know how to solve K-maps?
-Viewers who already know how to solve K-maps are encouraged to watch the entire lecture because it will provide insights into the theoretical aspects and internal workings of K-maps, improving their overall comprehension.
How does the K-map relate to logic minimization?
-The K-map is a tool used for logic minimization by visually simplifying Boolean expressions. It helps in reducing complex expressions into simpler ones by finding patterns in the truth table and grouping terms that can be combined.
What will viewers learn about K-maps in this presentation?
-Viewers will learn the basics of K-maps, including how they function, how to use them for logic simplification, and the importance of grouping terms in the K-map to achieve a simplified Boolean expression.
What does the presenter mean by 'a very simple way to understand K-maps'?
-The presenter emphasizes that the approach will be straightforward and easy to follow, ensuring that even beginners can grasp the concept of K-maps without feeling overwhelmed by complex details.
Why is understanding K-maps important for solving Boolean logic problems?
-Understanding K-maps is crucial for solving Boolean logic problems because they provide an intuitive visual tool to minimize logical expressions, which leads to simpler, more efficient digital circuits.
What makes K-maps different from other methods of simplifying Boolean expressions?
-K-maps differ from other methods, such as algebraic manipulation, by offering a visual approach that makes it easier to identify simplifications and avoid mistakes that might occur when working purely with algebraic methods.
What is the expected outcome for someone who watches this presentation until the end?
-By watching the presentation until the end, viewers will not only learn how to solve K-maps but also gain a deeper understanding of the logic and principles behind them, leading to better problem-solving skills in Boolean simplification.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Minimize the given Boolean Function using K-Map then Implement Using Basic Gates | By Mathur Sir
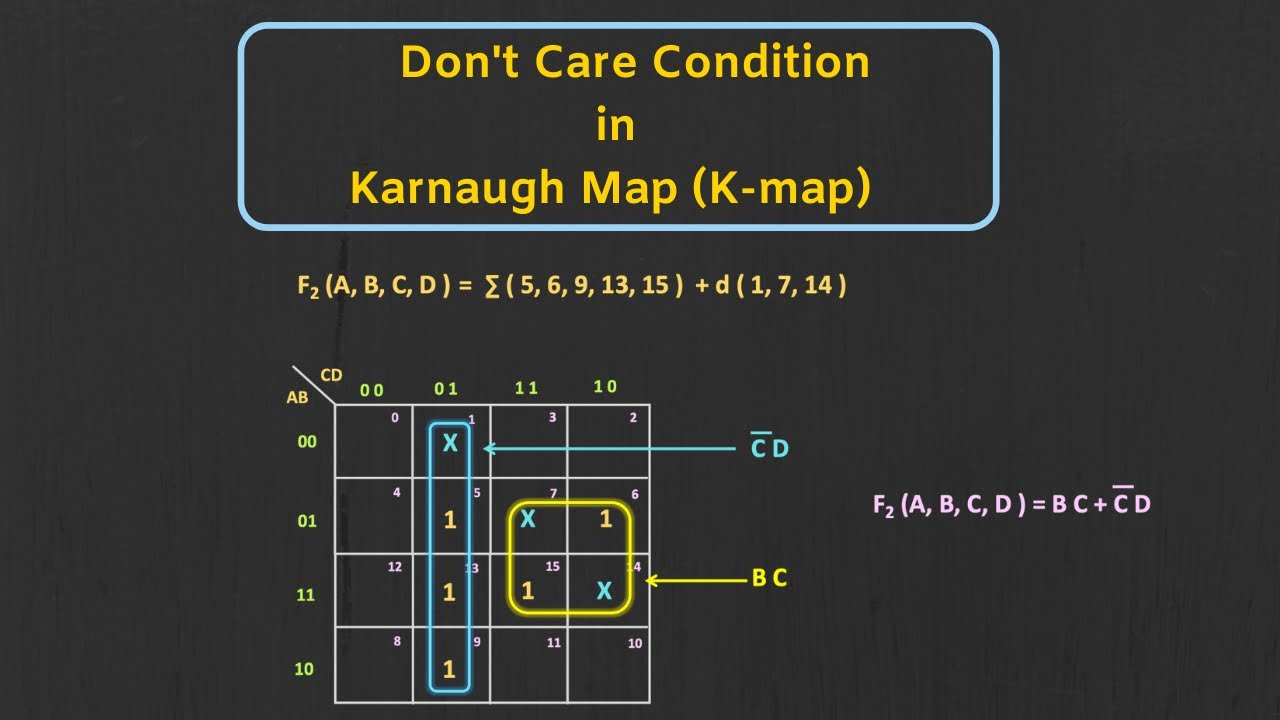
Don't Care Conditions in Karnaugh Map (with Solved Examples)
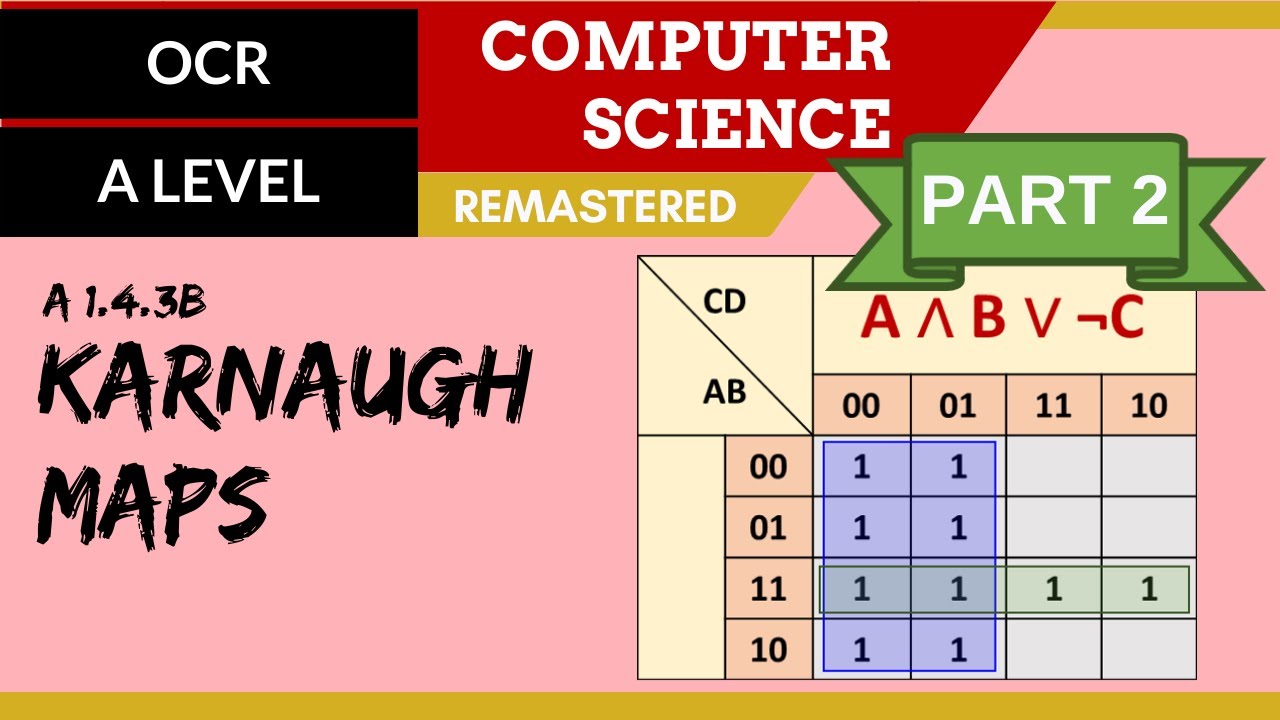
99. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 2

Priority Encoder
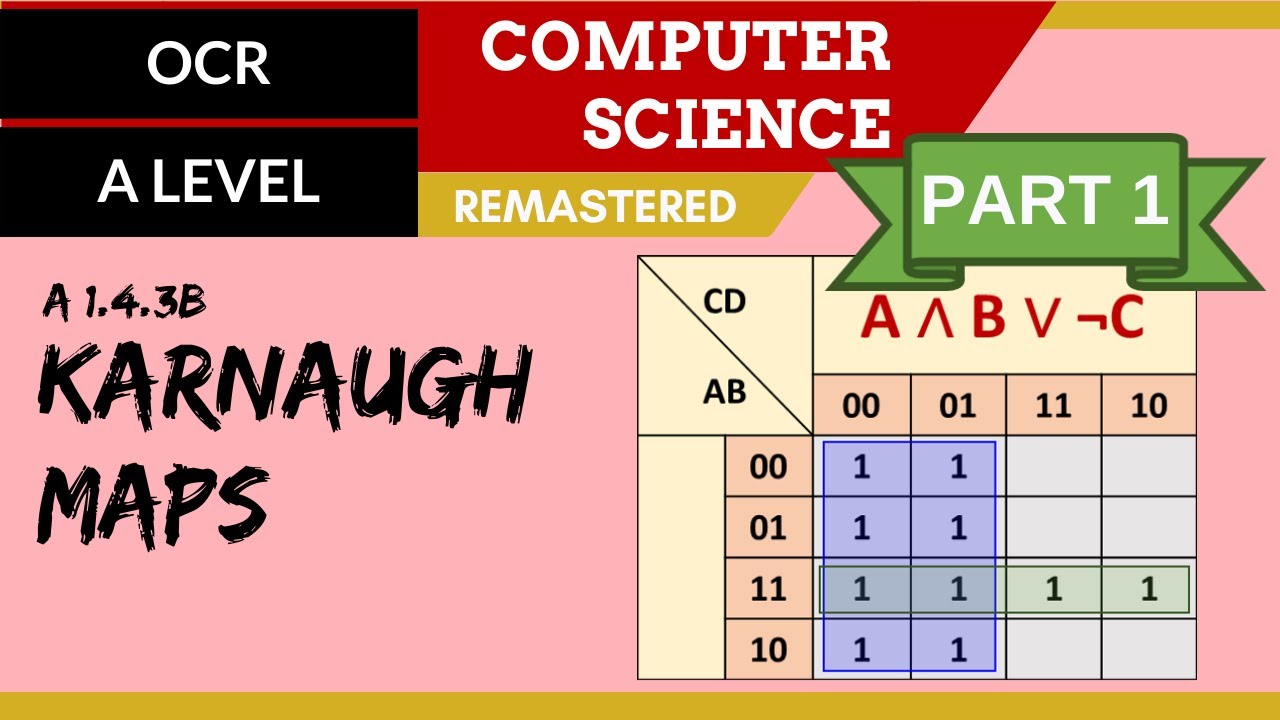
98. OCR A Level (H046-H446) SLR15 - 1.4 Karnaugh maps part 1

3-Variable K-Map | Minimization of 3-Variable POS Function Using K-Map | By Mathur Sir
5.0 / 5 (0 votes)
