Einstein's proof of Pythagoras theorem
Summary
TLDRThis video presents an elegant proof of the Pythagorean Theorem, originally proposed by Einstein, through geometric methods. It begins by explaining the relationship between the sides of a right triangle and the areas of squares drawn on each side. The video explores the use of semicircles and similar triangles to demonstrate that the area of the hypotenuse’s semicircle equals the sum of the areas of the other two shapes. The proof ultimately proves the theorem by showing how areas on the triangle’s sides relate, offering an insightful and accessible approach to understanding this fundamental concept in geometry.
Takeaways
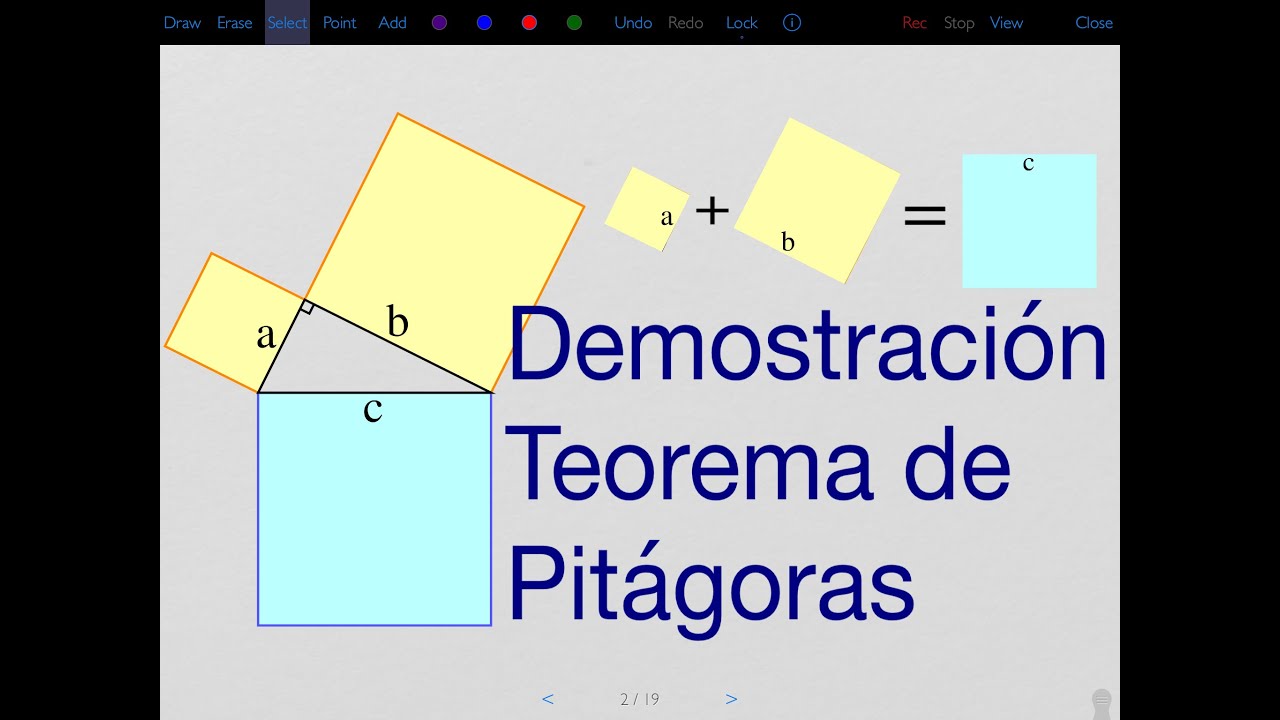
- 😀 The Pythagoras Theorem states that in a right-angled triangle, the square of the hypotenuse (side c) equals the sum of the squares of the other two sides (a and b), i.e., c² = a² + b².
- 😀 The theorem is commonly illustrated by drawing squares on each side of the triangle, with their areas representing the squares of the side lengths.
- 😀 Einstein's proof of the Pythagoras Theorem offers a more elegant and simple approach that does not rely on using squares, but on geometric shapes like semicircles and similar triangles.
- 😀 In Einstein's proof, semicircles are drawn on each side of the triangle, and their areas are used to establish the relationship between the side lengths.
- 😀 The area of a semicircle is calculated as (π * r²) / 2, where r is the radius. For the semicircles on sides a, b, and c, the areas are proportional to a², b², and c², respectively.
- 😀 By summing the areas of the semicircles on sides a and b, the result equals the area of the semicircle on side c, which is a visual proof of the Pythagoras Theorem.
- 😀 The theorem can also be proven using similar triangles. Drawing a perpendicular line from the hypotenuse to the opposite vertex divides the original triangle into three smaller, similar triangles.
- 😀 Two triangles are considered similar if they have the same shape, with corresponding angles equal and side lengths in proportion.
- 😀 The similar triangles formed by the perpendicular line have hypotenuses of length a, b, and c, and they are used to prove that the areas of the smaller triangles add up to the area of the larger triangle.
- 😀 By demonstrating that the areas of the triangles on sides a and b add up to the area on side c, Einstein's proof confirms the validity of the Pythagoras Theorem.
- 😀 Einstein's proof emphasizes the use of geometric constructs and similarity relationships between triangles to intuitively prove the Pythagoras Theorem without relying on algebraic methods.
Q & A
What is the Pythagoras Theorem?
-The Pythagoras Theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side, 'c') is equal to the sum of the squares of the other two sides ('a' and 'b'). The equation is: c² = a² + b².
How can the Pythagoras Theorem be illustrated geometrically?
-The Pythagoras Theorem can be visually illustrated by drawing squares on each side of a right triangle. The area of the square on side 'a' is a², the area of the square on side 'b' is b², and the area of the square on side 'c' is c². The theorem shows that the area of the square on the hypotenuse (c²) equals the sum of the areas of the squares on the other two sides (a² + b²).
What is the significance of using semicircles in the proof?
-In the proof, semicircles are used as an alternative to squares. By calculating the area of the semicircles drawn on each side of the triangle, the relationship between their areas (π/8 * c² = π/8 * (a² + b²)) illustrates the same mathematical relationship as the Pythagorean Theorem, thereby validating the equation.
How are the areas of the semicircles related to the sides of the triangle?
-The area of a semicircle is calculated using the formula (π/8) * r², where 'r' is the radius. For each side of the triangle, the radius is half the length of the respective side. Therefore, for side 'a', the area of the semicircle is (π/8) * a², and similarly for sides 'b' and 'c'. The sum of the areas of the semicircles on sides 'a' and 'b' equals the area of the semicircle on side 'c'.
What role do similar triangles play in the proof?
-In the proof, drawing a perpendicular from the hypotenuse to the opposite vertex creates three similar triangles. These triangles share the same angles as the original triangle, and their areas can be used to show that the sum of the areas of the shapes on sides 'a' and 'b' is equal to the area of the shape on side 'c'.
Why are the three triangles formed in the proof considered similar?
-The three triangles formed by drawing a perpendicular from the hypotenuse to the opposite vertex are considered similar because they all share the same angles as the original right triangle. This similarity arises from having two equal angles and being right-angled triangles.
How does the use of similar triangles lead to the proof of the Pythagoras Theorem?
-By proving that the areas of the shapes on sides 'a' and 'b' can be combined to form the area on side 'c', the similarity of the triangles helps to confirm that the sum of the squares of the two shorter sides ('a' and 'b') is equal to the square of the hypotenuse ('c').
What is the significance of the equation 'π/8 * c² = π/8 * (a² + b²)'?
-The equation 'π/8 * c² = π/8 * (a² + b²)' demonstrates that when both sides of the Pythagoras Theorem are multiplied by the constant π/8, the relationship still holds true. This equation effectively proves that the area of the semicircle on the hypotenuse is equal to the sum of the areas of the semicircles on the other two sides, which is another way of expressing the Pythagoras Theorem.
How does Einstein's proof differ from other proofs of the Pythagoras Theorem?
-Einstein's proof is notable for using geometric shapes such as squares, semicircles, and similar triangles to prove the Pythagoras Theorem. Unlike algebraic proofs, this approach relies heavily on visual and geometric reasoning to demonstrate the relationship between the areas and the sides of the triangle.
What is the final conclusion of the proof presented in the video?
-The final conclusion of the proof is that the sum of the areas of the shapes on the two shorter sides ('a' and 'b') is equal to the area of the shape on the hypotenuse ('c'). This proves the Pythagoras Theorem, confirming that c² = a² + b².
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)