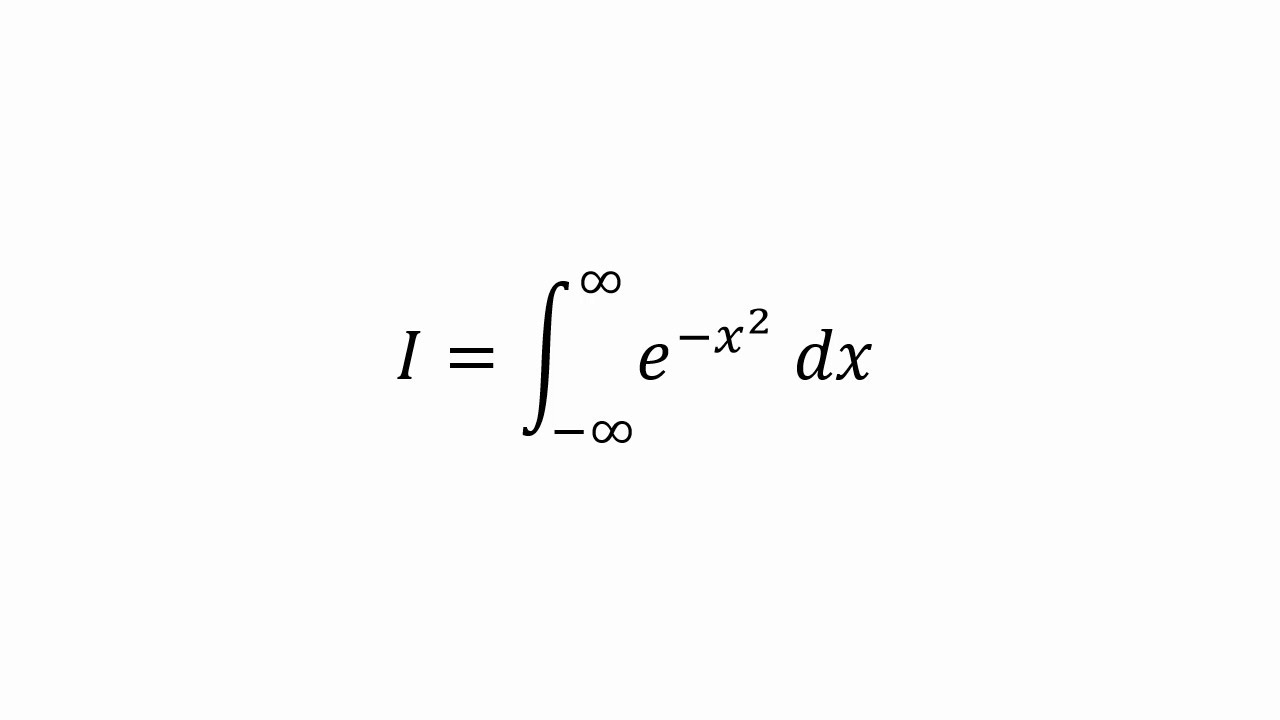Lecture 32 : Improper Integral – Part 2

Summary

本讲座详细讲解了积分的比较测试方法，尤其是如何通过比较函数的积分来判断其收敛性或发散性。讲解中介绍了两种主要的比较测试：一种是通过函数的上界和下界来比较积分的收敛性，另一种是通过函数间的增长率来判断积分行为的相似性。通过具体例子，演示了如何利用比较测试得出积分收敛或发散的结论，帮助学生更好地理解如何应用这些数学工具解决实际问题。

Takeaways

• 😀 比较测试可以用来分析积分的收敛性或发散性。
• 😀 第一个比较测试表明，如果一个较大函数的积分收敛，较小函数的积分也会收敛。
• 😀 第二个比较测试表明，如果较大函数的积分发散，较小函数的积分也会发散。
• 😀 可以通过调整常数（例如将2改为4）来确保函数始终保持正值，从而进行有效的比较。
• 😀 在应用比较测试时，首先需要确保被比较的函数满足适当的条件，比如大于等于零。
• 😀 比较测试2表明，如果两个函数的比值趋近于一个常数k，那么这两个积分的行为将类似。
• 😀 如果常数k为0且较大函数的积分收敛，那么较小函数的积分也会收敛。
• 😀 如果常数k为无穷大且较大函数的积分发散，那么较小函数的积分也会发散。
• 😀 通过选择合适的函数进行比较，可以更简便地确定积分的收敛性。
• 😀 通过这两种比较测试方法，可以推导出复杂函数积分的收敛性或发散性。
• 😀 该讲座总结了关于比较测试的两个重要结论，并提供了多个实例加以说明。

Q & A

什么是比较测试？

比较测试是一种数学方法，用于通过将目标函数与其他已知收敛或发散的函数进行比较，来判断一个积分的收敛性或发散性。

如何应用比较测试？

通过找出一个函数（如f(x)）与另一个已知的函数（如g(x)）之间的关系，确保f(x)在某些区间内小于等于g(x)，然后利用g(x)的积分收敛性或发散性来推断f(x)的积分行为。

什么是比较测试1？

比较测试1指出，如果g(x) ≥ f(x)，并且g(x)的积分收敛，那么f(x)的积分也会收敛；如果f(x)的积分发散，则g(x)的积分也会发散。

什么是比较测试2？

比较测试2涉及函数f(x)与g(x)的比值lim(x→∞) f(x)/g(x)的极限。如果该极限是常数且不为0，那么两个积分的行为相同；如果极限为0且g(x)的积分收敛，则f(x)的积分也收敛；如果极限为∞且g(x)的积分发散，则f(x)的积分也发散。

比较测试如何帮助判断积分收敛性？

通过比较f(x)和g(x)的行为，我们可以通过已知函数的积分结论来推测未知函数的积分结论。如果较大的函数g(x)的积分收敛或发散，我们就可以得出f(x)积分的结论。

如何处理包含负值的函数？

在应用比较测试时，我们通常希望函数f(x)的值为非负值，以确保比较过程的有效性。可以通过调整函数的常数项或改变函数的参数来实现这一点。

在比较测试中，如何选择合适的g(x)？

选择g(x)时，要确保g(x)在目标区间内大于或等于f(x)，并且g(x)的积分已知能够收敛或发散，这样可以借助g(x)的性质来推断f(x)的积分行为。

如何理解测试中提到的“k”值？

在比较测试2中，k是f(x)和g(x)比值的极限。如果k不为0且是常数，则两个积分的行为相同。如果k为0且g(x)的积分收敛，则f(x)的积分也收敛；如果k趋向于无穷且g(x)发散，则f(x)也会发散。

函数的增长速度如何影响比较测试的结论？

如果函数g(x)比f(x)增长得更快，且g(x)的积分收敛，则f(x)的积分也会收敛。反之，如果g(x)的积分发散，则f(x)的积分也会发散。

为什么比较测试对积分收敛性判断如此重要？

比较测试提供了一种简便的方法来判断复杂函数的积分收敛性。通过与已知的简单函数进行比较，我们可以避免直接计算复杂积分，从而得到快速且准确的结论。