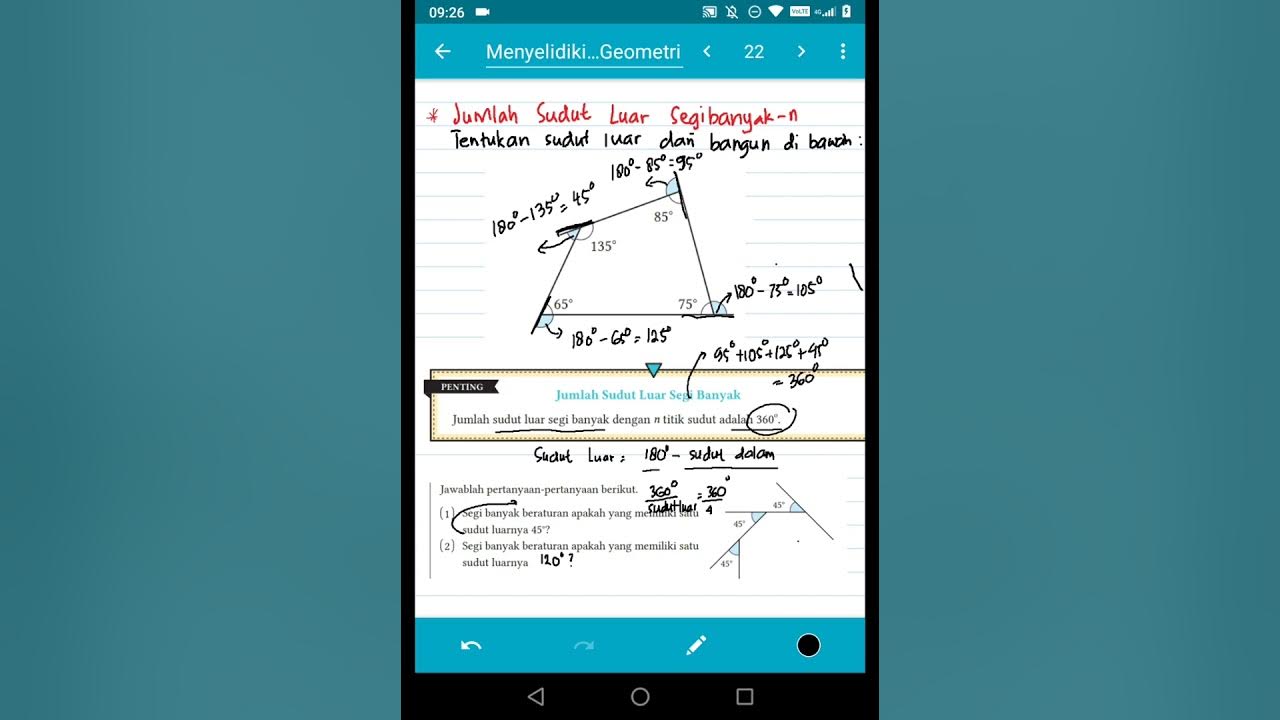
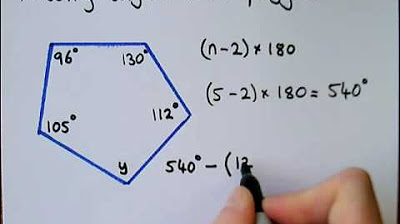
Suma de ángulos internos de un polígono

Summary

In this video, the presenter explains how to calculate the sum of internal angles in a convex polygon. The formula involves multiplying 180 degrees by the number of sides minus 2. Several examples are provided, starting with a quadrilateral and progressing to polygons with more sides. For each case, the number of sides (n) is identified, and the formula is applied to find the sum of angles. The video concludes with an exercise, encouraging viewers to calculate the sum of angles for polygons with eight and twenty sides.

Takeaways

• 😀 The sum of the interior angles of any convex polygon can be calculated using the formula: 180° × (n - 2), where n is the number of sides.
• 😀 To calculate the sum of the interior angles of a polygon, substitute the number of sides (n) into the formula.
• 😀 For a quadrilateral (4 sides), the sum of the interior angles is 360° (180° × (4 - 2) = 360°).
• 😀 For a polygon with 5 sides, the sum of the interior angles is 540° (180° × (5 - 2) = 540°).
• 😀 For a polygon with 16 sides, the sum of the interior angles is 2520° (180° × (16 - 2) = 2520°).
• 😀 The formula for finding the sum of interior angles is applicable to any convex polygon, regardless of the number of sides.
• 😀 The key component of the formula is (n - 2), which adjusts the calculation based on the number of sides in the polygon.
• 😀 To apply the formula correctly, it's important to first identify the number of sides (n) in the polygon.
• 😀 After applying the formula, the sum of the interior angles can be easily computed by multiplying 180° by (n - 2).
• 😀 The tutorial encourages practicing the formula with different polygons, such as one with 8 sides and one with 20 sides, to reinforce understanding.

Q & A

What is the formula for calculating the sum of interior angles in a polygon?

The formula for calculating the sum of the interior angles in a polygon is 180° × (n - 2), where 'n' is the number of sides of the polygon.

What does the 'n' represent in the formula for the sum of interior angles?

'n' represents the number of sides of the polygon.

How would you calculate the sum of interior angles for a quadrilateral using the formula?

For a quadrilateral, 'n' equals 4. The sum of the interior angles is calculated as 180° × (4 - 2), which is 180° × 2 = 360°.

Why does the formula subtract 2 from the number of sides (n - 2)?

The subtraction of 2 accounts for the fact that a polygon's interior angles are calculated from triangles. A polygon with 'n' sides can be divided into (n - 2) triangles, and the sum of angles in each triangle is 180°.

If a polygon has 5 sides, how would you find the sum of its interior angles?

For a polygon with 5 sides, 'n' equals 5. The sum of the interior angles is calculated as 180° × (5 - 2), which is 180° × 3 = 540°.

How do you calculate the sum of interior angles for a 16-sided polygon?

For a 16-sided polygon, 'n' equals 16. The sum of the interior angles is calculated as 180° × (16 - 2), which is 180° × 14 = 2520°.

What is the sum of the interior angles of a polygon with 8 sides?

For an 8-sided polygon, 'n' equals 8. The sum of the interior angles is calculated as 180° × (8 - 2), which is 180° × 6 = 1080°.

How can the sum of interior angles help us understand the properties of polygons?

The sum of interior angles provides insight into the overall geometry of the polygon. It helps in determining how the angles relate to each other based on the number of sides the polygon has, and it's essential in geometry for solving various problems related to polygons.

What is the sum of the interior angles for a polygon with 20 sides?

For a polygon with 20 sides, 'n' equals 20. The sum of the interior angles is calculated as 180° × (20 - 2), which is 180° × 18 = 3240°.

Can the formula for the sum of interior angles be used for any convex polygon?

Yes, the formula for the sum of interior angles (180° × (n - 2)) applies to all convex polygons, regardless of the number of sides.