Pertidaksamaan linear dua variabel kelas X. SOAL DAN PEMBAHASAN TRIK CEPAT. Part #1
Summary
TLDRIn this educational session, the instructor explains linear inequalities in two variables, focusing on solving and graphing these inequalities. Through detailed examples, such as X + 3Y > 6 and 5X + 2Y ≤ 10, the instructor demonstrates how to find intercepts, graph the corresponding lines (solid or dashed based on the inequality type), and shade the correct regions. The discussion emphasizes the importance of visual representation in understanding inequalities, encouraging students to practice these techniques for better comprehension.
Takeaways
- 😀 Understanding linear inequalities involves rewriting them as equations for easier manipulation.
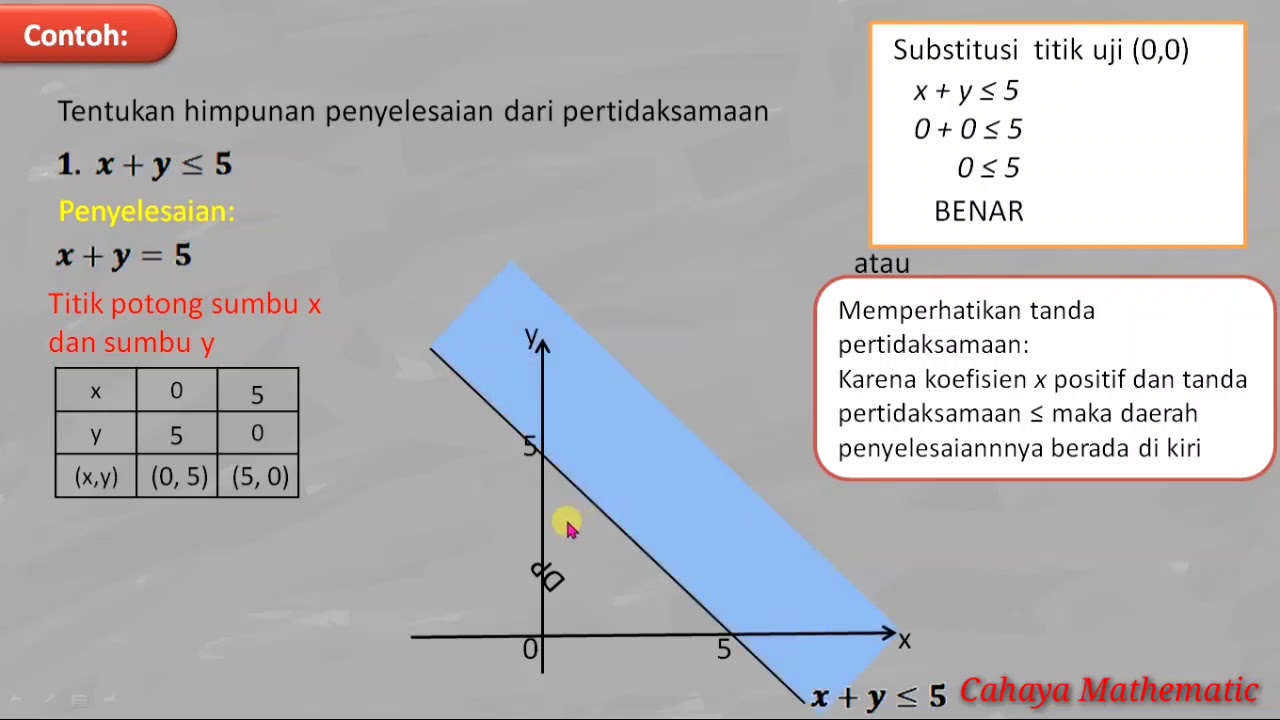
- 📊 Plotting points on a Cartesian graph is essential for visualizing solutions to inequalities.
- ✏️ A dashed line represents strict inequalities (e.g., > or <), while a solid line indicates inclusive inequalities (e.g., ≥ or ≤).
- 📏 To find boundary points, you can set one variable to zero and solve for the other, providing clear intersection coordinates.
- 🖊️ The two-point formula is crucial for determining the equation of the line that serves as the boundary for the inequality.
- 🔍 Shading regions on the graph helps identify where the inequality holds true: above the line for greater than and below for less than.
- ✅ The process of solving inequalities includes substituting values to check if points lie within the solution area.
- 📉 Understanding the relationship between the variables is key to interpreting the graph accurately.
- 💡 Quick methods for graphing can be developed with practice, enhancing efficiency in solving linear inequalities.
- 🧮 Practical examples illustrate how to apply theoretical concepts to real-world problems, reinforcing understanding.
Q & A
What is the primary topic discussed in the video?
-The primary topic is linear inequalities in two variables, specifically how to solve and graph them.
How do you begin solving the inequality x + 3y > 6?
-To begin solving the inequality, you can convert it to the equation 2x + 3y = 6 and find the intersection points.
What does a dashed line represent when graphing inequalities?
-A dashed line indicates that the boundary is not included in the solution set, meaning points on the line do not satisfy the inequality.
What method is suggested for finding points to plot on the graph?
-The instructor suggests substituting values for x and y, such as setting x = 0 or y = 0, to find intersection points for plotting.
Why is it important to understand the regions in relation to the origin when graphing?
-Understanding the regions in relation to the origin helps determine whether the solution set includes points that approach or move away from the origin based on the inequality.
What formula is used to determine the equation of the boundary line?
-The formula used is (y2 - y1) / (x2 - x1), which helps to find the slope and create the equation for the line based on two points.
How does the video suggest handling equations with more than one variable?
-The video suggests substituting one variable to isolate the other, making it easier to graph and find the solution.
What happens to the solution set if the inequality is changed from 'greater than' to 'less than'?
-If the inequality changes from 'greater than' to 'less than', the orientation of the shaded region on the graph also changes, affecting which side of the boundary line represents the solution.
Can you explain the significance of solid lines in graphing inequalities?
-Solid lines indicate that the boundary is included in the solution set, meaning points on the line satisfy the inequality.
What does the instructor mention about the approach to teaching graphing methods?
-The instructor emphasizes teaching conventional methods before introducing quicker techniques for determining graphs, ensuring a solid foundational understanding.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

SPtDV Matematika Kelas 10 • Part 1: Pertidaksamaan Linear & Kuadrat Dua Variabel

Menyelesaikan Permasalahan Program Linear Menentukan Nilai Optimum dengan Metode Uji Titik Pojok

cara cepat sistem pertidaksamaan linier dua variabel dari grafik

MENENTUKAN MODEL MATEMATIKA DARI SOAL CERITA SPtLDV
PERTIDAKSAMAAN LINEAR DUA VARIABEL

Soal & Pembahasan SPTLDV Sistem Pertidaksamaan Linear Dua Variabel SOAL CERITA
5.0 / 5 (0 votes)
