Solving Quadratic Inequalities - Grade 9 Math Teacher Gon
Summary
TLDRIn this educational video, Teer explains how to solve quadratic inequalities, focusing on two examples. He begins with the inequality x² + 7x + 10 ≤ 0, identifying critical points and using a number line to determine valid solution regions. Teer emphasizes the importance of including or excluding critical points based on the inequality's symbols. The video then moves to a second example, x² + 3x - 10 < 0, where Teer showcases the process of finding solutions and illustrates how to express them in interval notation. Viewers are encouraged to like and subscribe for more math content.
Takeaways
- 😀 Quadratic inequalities can be solved by first converting them into quadratic equations.
- 😀 The critical points are found by factoring the quadratic equation and setting each factor to zero.
- 😀 It's important to represent critical points accurately on a number line, including whether they are included in the solution or not.
- 😀 Use solid circles for critical points included in the solution and open circles for those that are not included.
- 😀 The number line is divided into regions based on critical points, which helps in testing for valid solutions.
- 😀 Selecting test points from each region determines if that region satisfies the inequality.
- 😀 If a test point results in a true statement when substituted back into the inequality, that region is part of the solution.
- 😀 For solutions in interval notation, use brackets [] for included critical points and parentheses () for excluded points.
- 😀 The method demonstrated can be applied to both strict inequalities (< or >) and non-strict inequalities (≤ or ≥).
- 😀 Understanding the process of solving quadratic inequalities is essential for advanced algebra topics and real-world applications.
Q & A
What is the first step in solving a quadratic inequality?
-The first step is to convert the inequality into a quadratic equation by replacing the inequality sign with an equal sign.
How do you determine the critical points of a quadratic inequality?
-Critical points are found by factoring the quadratic equation and setting each factor equal to zero.
What notation is used to indicate that critical values are included in the solution?
-A solid circle is used to indicate that critical values are included in the solution, while an open circle is used if they are not included.
How do you divide the number line for quadratic inequalities?
-The number line is divided into regions based on the critical points, allowing you to test values from each region to see if they satisfy the inequality.
What is a representative value in the context of solving quadratic inequalities?
-A representative value is a test value chosen from each region of the number line to determine whether that region is part of the solution.
How do you interpret the results after testing the regions?
-The interpretation of the results is based on which regions yield true statements when the representative values are substituted back into the original inequality.
What does it mean if a region is determined to be a solution?
-If a region is a solution, it means all values of x within that region satisfy the inequality.
What is interval notation, and how is it used in the context of quadratic inequalities?
-Interval notation is a way of representing solutions of inequalities, using brackets to indicate included endpoints and parentheses for excluded endpoints.
In the second example, why were the critical values not included in the solution?
-The critical values were not included because the inequality was strictly less than (not less than or equal to), which requires open circles on the graph.
Can you summarize the solutions of the two examples given in the video?
-For the first example, the solution is [-5, -2], indicating that both -5 and -2 are included. For the second example, the solution is (-5, 2), meaning neither -5 nor 2 is included.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

SPtDV Matematika Kelas 10 • Part 1: Pertidaksamaan Linear & Kuadrat Dua Variabel

Half Past Paper - Week 2 - Higher Edexcel GCSE Maths - Maths Revision
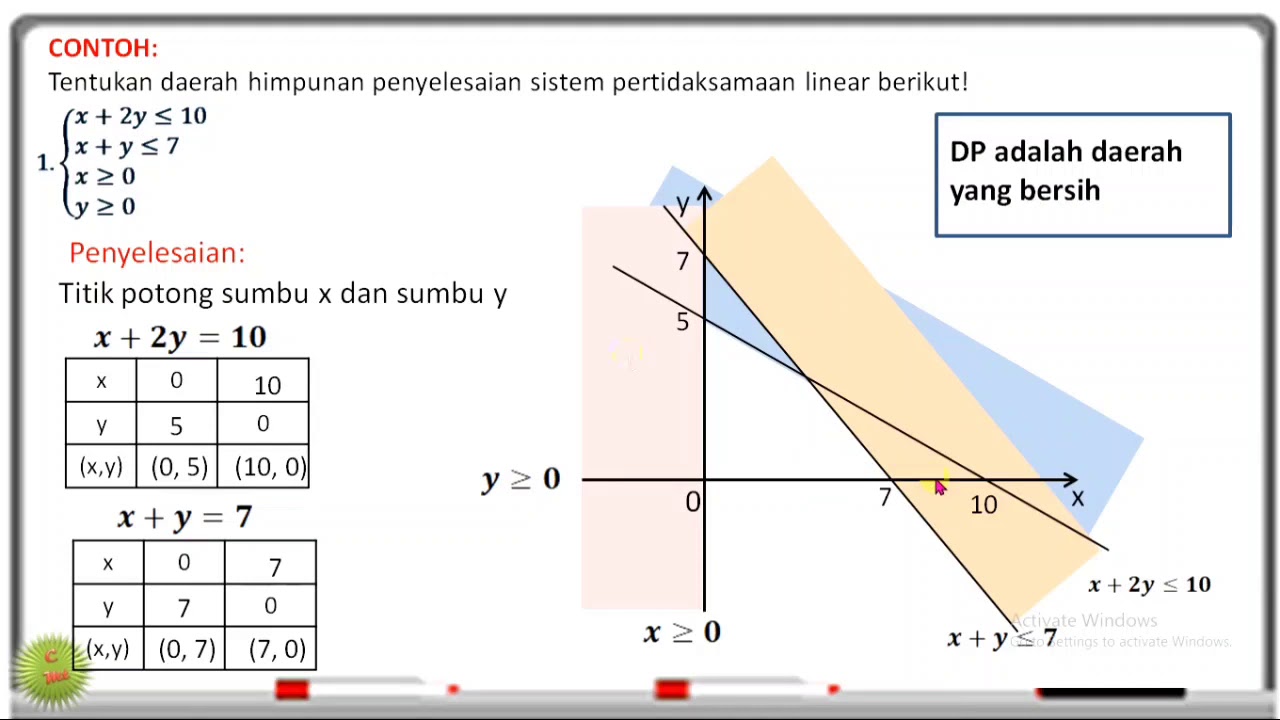
SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL SPtLDV

Jenis-jenis akar persamaan kuadrat || akar real berbeda, akar real sama, akar tidal real (IMAJINER)
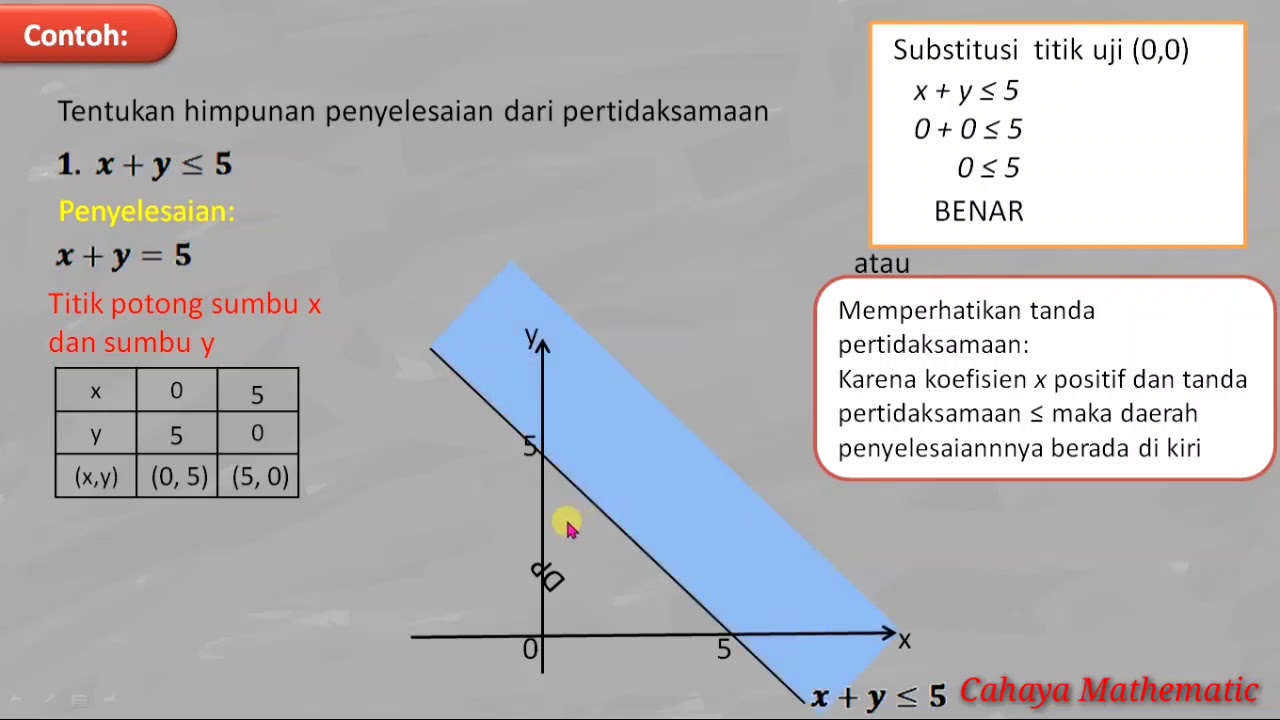
PERTIDAKSAMAAN LINEAR DUA VARIABEL
Solving Quadratic Inequalities - GCSE Higher Maths
5.0 / 5 (0 votes)
