Derivada del cociente de dos funciones (u/v)
Summary
TLDREn este video, se explica cómo derivar el cociente de dos funciones utilizando la fórmula adecuada. El presentador desglosa el proceso paso a paso, comenzando por identificar el numerador y el denominador de la función. Se derivan cada uno de los términos, aplicando las reglas de derivación, y se realizan multiplicaciones y restas para simplificar el resultado final. Con un ejemplo práctico de derivar la función (5x + 2) / (3x + 8), el video proporciona una comprensión clara de cómo aplicar las técnicas de cálculo diferencial de manera efectiva.
Takeaways
- 😀 Bienvenida a la continuación del tema de cálculo diferencial.
- 📐 Se aborda la derivada del cociente de dos funciones.
- 📝 Fórmula de la derivada de un cociente: (u/v)' = (v * u' - u * v') / v^2.
- 🔍 Ejemplo práctico: derivar la función (5x + 2) / (3x + 8).
- 📊 Identificación de funciones: u = 5x + 2, v = 3x + 8.
- ➕ Derivadas calculadas: u' = 5, v' = 3.
- 🔄 Aplicación de la fórmula para obtener la derivada.
- ✏️ Se realizan multiplicaciones y simplificaciones en el proceso.
- 🧮 Resultado final de la derivada: (34) / (3x + 8)^2.
- 👋 Cierre del tema con un saludo a los amigos.
Q & A
¿Cuál es el tema principal de la sesión?
-La sesión se centra en la derivada del cociente de dos funciones en cálculo diferencial.
¿Cuál es la fórmula para derivar el cociente de dos funciones?
-La fórmula es: d/dx(u/v) = (v * du/dx - u * dv/dx) / v^2.
¿Cómo se identifica el numerador y el denominador en el ejemplo proporcionado?
-En el ejemplo, el numerador es 5x + 2 y el denominador es 3x + 8.
¿Qué es lo primero que se hace al aplicar la fórmula de derivación?
-Se identifican las funciones u y v y se encuentran sus derivadas.
¿Cuál es la derivada de 5x y por qué?
-La derivada de 5x es 5 porque se utiliza la regla de derivación de una constante multiplicada por x.
¿Qué ocurre con la derivada de una constante?
-La derivada de una constante es 0, por lo que la derivada de 2 es 0.
¿Cuál es el resultado de la multiplicación de los términos al aplicar la fórmula?
-Se obtiene 15x + 40 - 15x - 6, que simplificado es 34.
¿Cómo se simplifica el resultado final?
-El resultado se simplifica a 34 sobre (3x + 8)^2 después de restar los términos.
¿Cuál es el resultado final de la derivada en el ejemplo?
-El resultado final de la derivada es 34 / (3x + 8)^2.
¿Cuál es la importancia de entender cómo derivar el cociente de dos funciones?
-Es importante porque permite resolver problemas más complejos en cálculo y aplicaciones en diversas áreas de las matemáticas y la física.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Derivada de un cociente | Reglas de derivación

Derivada de un producto o multiplicación de funciones. Cálculo diferencial
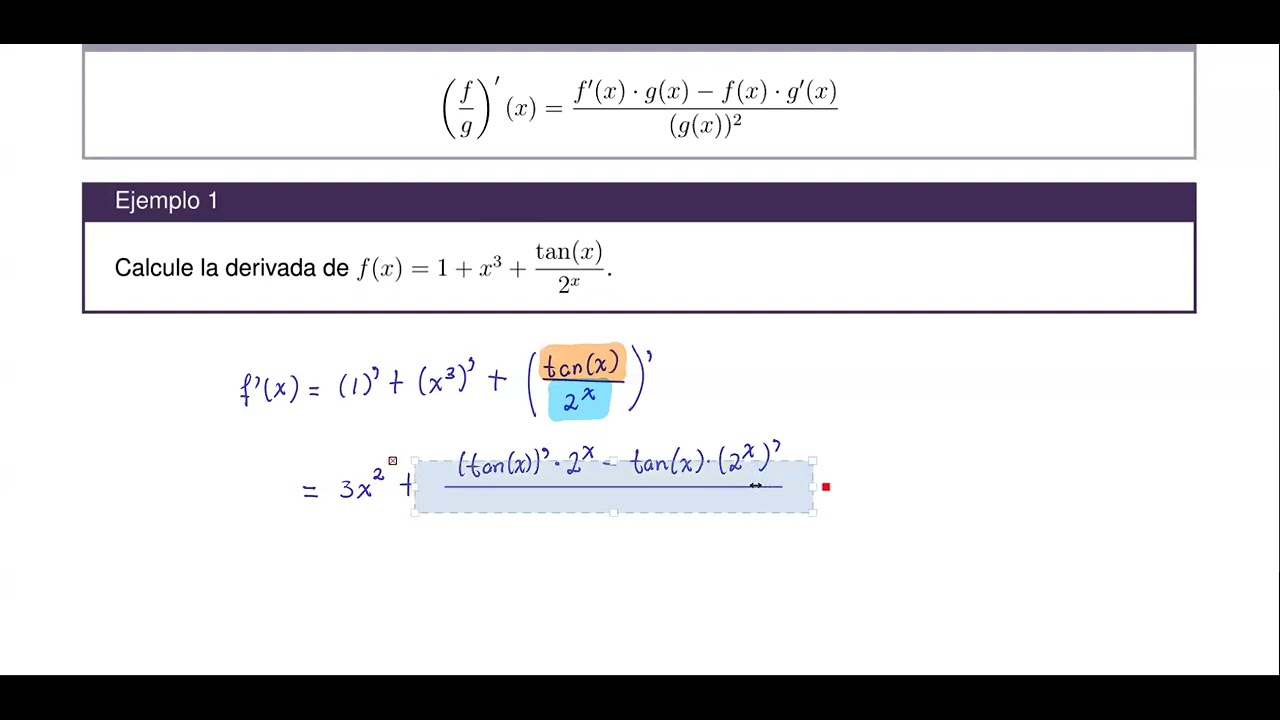
Derivadas (Regla del cociente) 1

CÓMO SE DERIVADA UNA FUNCIÓN PARAMÉTRICA - DERIVADA de FUNCIÓN PARAMÉTRICA #2

Derivadas de orden superior - Ej. 2

REGLAS DE DERIVACIÓN - Repaso en 7 minutos con ejemplos
5.0 / 5 (0 votes)
