CB2201 Operations Management - Lecture 07 Queueing Model
Summary
TLDRIn this lecture, Sally explains the MMC (Multi-Server Queuing) model within the context of operations management, emphasizing its application in designing optimal service capacity. She details key parameters such as arrival rates, service rates, and the number of servers, illustrating their impact on customer waiting times. By introducing Little’s Law, she highlights the relationship between the number of customers in the system and their waiting time. The discussion includes real-life applications, the effects of variability on queues, and strategies to minimize waiting times, making this model a vital tool for effective service management.
Takeaways
- 😀 The importance of communication skills in personal and professional settings cannot be overstated.
- 🤝 Active listening enhances relationships and shows respect for others' opinions.
- 📝 Non-verbal cues, such as body language and eye contact, play a significant role in effective communication.
- 📚 Practicing public speaking can boost confidence and reduce anxiety.
- 💬 Tailoring your message to your audience improves understanding and engagement.
- 🔄 Feedback is essential for growth and helps refine communication techniques.
- 🗣️ Clarity and conciseness are key; avoid jargon to make your message accessible.
- 🧠 Emotional intelligence aids in navigating complex social situations and improving interactions.
- 💡 Using stories and examples can make your message more relatable and memorable.
- 🎯 Setting clear goals for communication helps focus discussions and achieve desired outcomes.
Q & A
What is the main topic of the lecture discussed in the video?
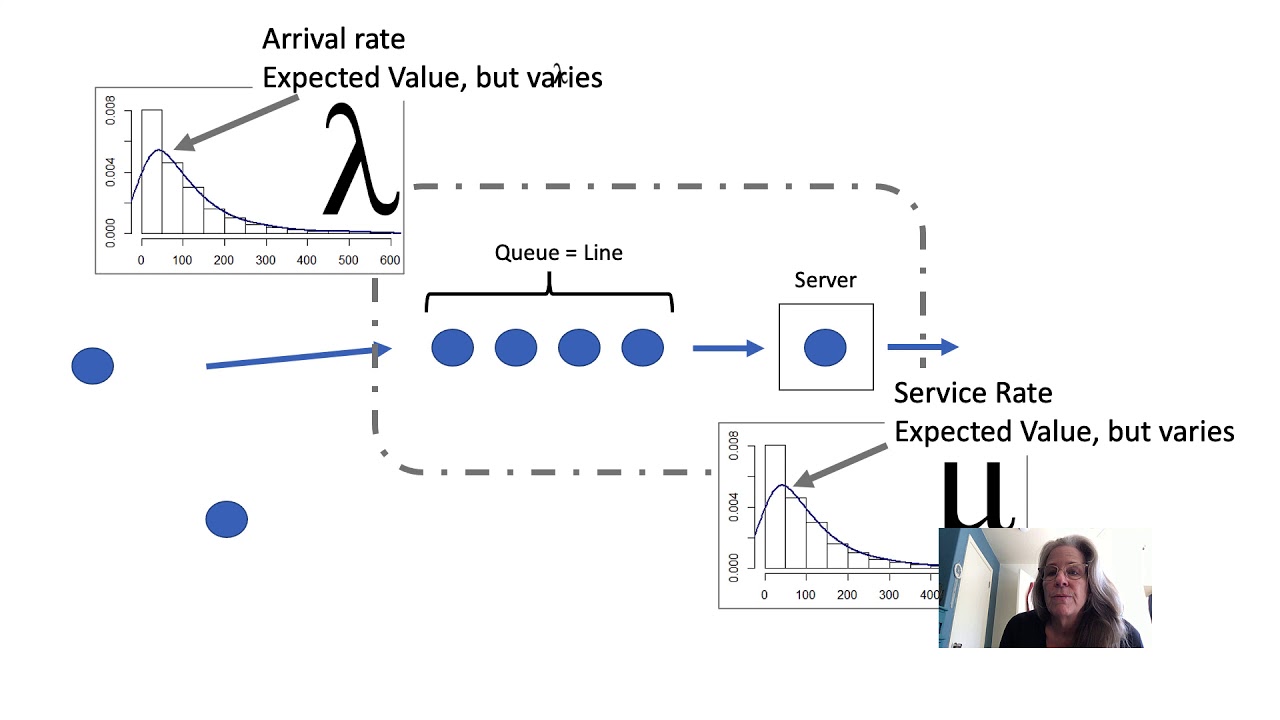
-The lecture discusses the M/M/c queuing model as part of operations management, focusing on how to design optimal service capacity.
What challenges do managers face when scheduling employees in a service environment?
-Managers need to balance the number of staff to avoid long customer wait times and high salary costs.
What does the 'M' in M/M/c stand for?
-'M' stands for 'memoryless', indicating that both arrival times and service times follow an exponential distribution.
How is the arrival rate represented in queuing models?
-The arrival rate is represented by the Greek letter λ (lambda), which indicates the number of customers arriving per unit of time.
What is the significance of Little's Law in queuing theory?
-Little's Law states that the average number of customers in a system (L) equals the arrival rate (λ) multiplied by the average waiting time in the system (W).
What factors can lead to increased waiting times in a queuing system?
-Increased variability in customer arrival and service times can lead to longer waiting times due to randomness.
Why might the M/M/c model not perfectly represent all queuing systems?
-The M/M/c model is a simplification and may not account for all real-life factors, such as variability in service times or multiple queues.
What are the three primary methods mentioned for reducing queue length and waiting times?
-The three methods are: reducing service time (increasing service rate μ), increasing the number of servers (c), and decreasing variability in arrival and service times.
In the context of the lecture, how is service rate μ calculated?
-Service rate μ is calculated by taking the reciprocal of the average service time per customer, converting it to the number served per unit time.
What is an example of a real-world application of the M/M/c queuing model provided in the lecture?
-The model can be applied in a Starbucks coffee store to determine the optimal number of employees needed to minimize customer wait times and salary costs.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)