Proyecto de ciencias para demostrar el MRUA - parte #2
Summary
TLDREste video ofrece una guía detallada sobre cómo construir un plano inclinado y medir el movimiento rectilíneo uniformemente acelerado. Se comienza calculando los ángulos de inclinación con un triángulo rectángulo, asumiendo un ángulo de 5 grados para este caso. Luego, se construye la rampa y se utiliza un cronómetro para medir el tiempo que tarda una canica en desplazarse a través de intervalos de 30, 60 y 90 centímetros. Los datos se registran y se analizan en una hoja de cálculo para encontrar el promedio de tiempos y construir una gráfica de desplazamiento versus tiempo. Finalmente, se calcula la aceleración utilizando la ecuación del movimiento y se grafica la relación entre el tiempo al cuadrado y la aceleración. El video concluye con la demostración de cómo, a partir de un plano inclinado, se puede calcular la aceleración, ofreciendo un proyecto práctico para el aprendizaje de física.
Takeaways
- 📐 La construcción de un plano inclinado se utiliza para demostrar el movimiento rectilíneo uniformemente acelerado.
- 📏 Se asume un ángulo de inclinación de 5 grados para este experimento, lo cual es recomendable para ángulos pequeños.
- 📐 La altura del plano inclinado se determina usando la función trigonométrica seno, aplicado al ángulo de inclinación.
- 🔍 Se utiliza un libro, una cajita desarmadores y tablas de MDF para construir el plano inclinado con la altura específica.
- ⏱️ Se toman mediciones de tiempo para diferentes intervalos de desplazamiento (30, 60 y 90 centímetros) y se repiten para mayor precisión.
- 📊 Los datos recolectados se analizan y grafican en una hoja de cálculo para visualizar el desplazamiento en función del tiempo.
- 📈 La gráfica resultante muestra un patrón de movimiento rectilíneo uniformemente acelerado, con una ecuación que representa el desplazamiento en función del tiempo al cuadrado.
- ⚙️ La aceleración se calcula a partir de la ecuación del movimiento, considerando que el desplazamiento es proporcional al tiempo al cuadrado.
- 📉 Se calcula el promedio de la aceleración obtenida de los intervalos de desplazamiento, proporcionando un valor promedio de aceleración para el experimento.
- 🔢 El valor de aceleración encontrado es específico para el ángulo de inclinación de 5 grados utilizado en el experimento.
- 📚 El proyecto es una herramienta educativa para entender conceptos de física en el contexto de un plano inclinado y su relación con el movimiento acelerado.
Q & A
¿Qué es el objetivo principal del video?
-El objetivo principal del video es continuar con la construcción de un plano inclinado para demostrar el movimiento rectilíneo uniformemente acelerado, hallar la aceleración y construir el gráfico de desplazamiento versus tiempo.
¿Cómo se calcula la altura de la rampa en función del ángulo de inclinación?
-Se utiliza un triángulo rectángulo para determinar la altura de la rampa. Conociendo la longitud de la hipotenusa (90 cm) y asumiendo un ángulo de inclinación de 5 grados, se calcula la altura como el seno del ángulo multiplicado por la longitud de la hipotenusa, dando como resultado aproximadamente 8 cm.
¿Qué instrumentos se utilizan para medir el desplazamiento de la canica en el plano inclinado?
-Se utilizan una canica, un plano inclinado con una altura específica, y un flexómetro para medir los desplazamientos a lo largo del plano.
¿Cómo se toman los tiempos de desplazamiento para cada intervalo?
-Se toman los tiempos de desplazamiento soltando la canica y utilizando un cronómetro para medir el tiempo que tarda en pasar por referencias marcadas a 30, 60 y 90 centímetros. Se realiza esta medición tres veces para cada intervalo.
¿Cómo se procesan los datos recolectados en una hoja de cálculo?
-Los datos recolectados se ingresan en una hoja de cálculo donde se calcula el promedio de los tiempos medidos para cada intervalo. Luego, se utilizan estas medias para construir una gráfica de desplazamiento versus tiempo.
¿Qué función se utiliza para modelar el movimiento en la gráfica de desplazamiento versus tiempo?
-Se utiliza una función cuadrática para modelar el movimiento, ya que el desplazamiento en un movimiento rectilíneo uniformemente acelerado es proporcional al tiempo al cuadrado.
¿Cómo se calcula la aceleración a partir de la gráfica de desplazamiento versus tiempo?
-Dado que el desplazamiento es proporcional al tiempo al cuadrado en un movimiento uniformemente acelerado, se despeja la aceleración (a) de la ecuación x = (1/2)at², encontrando así la aceleración para cada intervalo de tiempo y desplazamiento.
¿Qué significa el valor de R cuadrado en el contexto de la gráfica?
-El valor de R cuadrado, o el coeficiente de determinación, indica la calidad de la correlación entre las variables en la gráfica. Un valor cercano a 1 sugiere una correlación muy fuerte, lo que en este caso implica una buena ajuste de la curva cuadrática al modelo teórico del movimiento.
¿Por qué se recomienda utilizar ángulos pequeños para el plano inclinado?
-Se recomienda utilizar ángulos pequeños para facilitar los cálculos y para que la aproximación de los seno y coseno a los valores tangente en los triángulos rectángulos sea más precisa, simplificando así el análisis del movimiento.
¿Cómo se relaciona el valor de la aceleración calculada con la pendiente de la línea de tendencia en la gráfica?
-La pendiente de la línea de tendencia en la gráfica de desplazamiento versus tiempo al cuadrado representa la aceleración. Al calcular la pendiente se obtiene una ecuación que, una vez despejada, proporciona el valor de la aceleración.
¿Por qué es importante repetir las mediciones más de una vez?
-Repetir las mediciones varias veces ayuda a mejorar la precisión de los resultados al reducir el error experimental. Tomar el promedio de múltiples mediciones proporciona una valor más estable y confiables para el análisis.
¿Cómo se puede utilizar este experimento en un proyecto de ciencia?
-Este experimento puede utilizarse para demostrar conceptos de física como el movimiento uniformemente acelerado, la aceleración y la construcción de gráficas. Es útil para proyectos de ciencia que requieran una comprensión práctica de estos principios y para enseñar a los estudiantes a realizar mediciones y análisis de datos.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
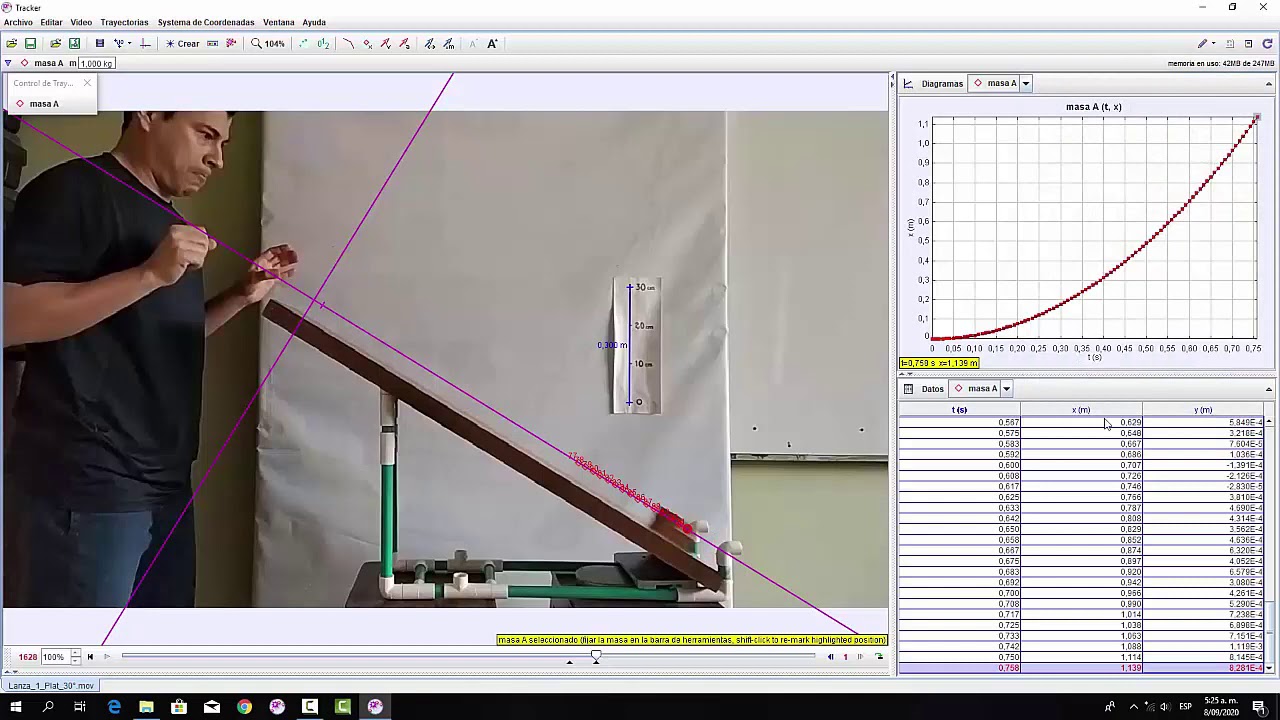
Tracker: Dinámica (Plano inclinado)

🚀 MRUA Movimiento Rectilíneo Uniformemente Acelerado | Explicación, fórmulas y ejercicios resueltos

Caída libre| movimiento vertical | formulas y ejemplos

Movimiento rectilíneo uniformemente acelerado - Introducción│ Física 8 de 28

Movimiento Parabólico

Movimiento Rectilíneo Uniformemente Acelerado o Variado MRUA MRUV | Ejemplo 5
5.0 / 5 (0 votes)
