Solución de problemas con Ecuaciones de Primer Grado | Ejemplo 14
Summary
TLDREl video explica cómo resolver problemas de ángulos en triángulos mediante lógica y ecuaciones. Primero, se introduce la relación entre los ángulos de un triángulo, resaltando que la suma siempre es 180 grados. Se utiliza un ejemplo donde uno de los ángulos mide el doble que otro y otro ángulo es 20 grados menos. El problema se resuelve primero por lógica y luego con ecuaciones, mostrando ambas formas. Finalmente, se presenta un ejercicio de práctica sobre un triángulo isósceles para que los espectadores lo intenten. El video anima a los usuarios a dejar sus propios problemas en los comentarios.
Takeaways
- 📐 La suma de los ángulos internos de cualquier triángulo siempre es 180 grados.
- 🔢 El problema del vídeo busca hallar los tres ángulos de un triángulo, donde A es el doble de B y C es 20 grados menos que B.
- 📝 Primero se intenta resolver el problema usando lógica, asumiendo valores para B, A y C.
- 🔍 Si B es 30 grados, A sería 60 grados (el doble de B) y C sería 10 grados (20 menos que B), pero la suma no es 180, por lo que se ajustan los valores.
- ✅ Al asumir que B es 50 grados, A sería 100 grados (el doble de B) y C sería 30 grados (20 menos que B), lo que suma 180 grados, siendo la solución correcta.
- ✏️ El problema también se resuelve usando ecuaciones. B es el ángulo base, A es el doble de B y C es B menos 20 grados.
- 🧮 La ecuación que representa la suma de los ángulos es B + 2B + (B - 20) = 180.
- ⚙️ Resolviendo la ecuación, se obtiene que B = 50 grados, lo que confirma los valores anteriores.
- 🎯 Finalmente, los ángulos son A = 100 grados, B = 50 grados y C = 30 grados.
- 📚 El vídeo invita a los espectadores a practicar con un ejercicio adicional sobre un triángulo isósceles.
Q & A
¿Cuál es la suma total de los ángulos internos de cualquier triángulo?
-La suma total de los ángulos internos de cualquier triángulo es siempre 180 grados.
Si en un triángulo, el ángulo A es el doble del ángulo B y el ángulo C es 20 grados menos que B, ¿cómo se puede calcular cada ángulo?
-Primero, se supone que B mide 50 grados, entonces A, que es el doble de B, mide 100 grados, y C, que es 20 grados menos que B, mide 30 grados. Así, los tres ángulos suman 180 grados.
¿Cómo se resuelve un problema geométrico utilizando ecuaciones?
-Primero se asignan letras a cada ángulo o variable. Luego, se escriben ecuaciones basadas en las relaciones dadas entre los ángulos, y finalmente se resuelven estas ecuaciones para encontrar los valores de los ángulos.
¿Qué es importante recordar sobre los ángulos en cualquier triángulo al resolver problemas?
-Es importante recordar que la suma de los ángulos internos de un triángulo siempre debe ser 180 grados.
¿Qué estrategia se utilizó en el video para resolver el problema de los ángulos antes de usar ecuaciones?
-Primero se utilizó la lógica, probando valores posibles para el ángulo B y calculando los otros ángulos basándose en las condiciones dadas.
¿Cómo se nombran usualmente los ángulos de un triángulo en geometría?
-Los ángulos de un triángulo generalmente se nombran con letras mayúsculas: A, B y C.
¿Qué debe cumplirse para que tres ángulos sean considerados los ángulos internos de un triángulo?
-Deben sumar exactamente 180 grados.
Si el ángulo A es el doble del ángulo B y el ángulo C es 20 grados menos que B, ¿qué ecuación se forma para resolver el problema?
-La ecuación sería: B + 2B + (B - 20) = 180, donde B es el ángulo más pequeño.
¿Qué pasos se deben seguir al resolver ecuaciones con ángulos de triángulos?
-Primero, se escriben las ecuaciones basadas en las relaciones dadas. Luego, se agrupan términos similares y se simplifican para encontrar los valores de los ángulos.
¿Cómo se comprueba la solución de un problema de ángulos en un triángulo?
-Se comprueba sumando los ángulos calculados y verificando que sumen 180 grados, y que las relaciones dadas (como que un ángulo sea el doble de otro) se cumplan.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Razones Trigonométricas

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera

Solución de problemas con Ecuaciones de Primer Grado | Ejemplo 8

Ángulos I - Operaciones con las medidas de ángulos y bisectriz de un ángulo - Geometría

How To Pass Geometry EOC (Tips + Strategies)
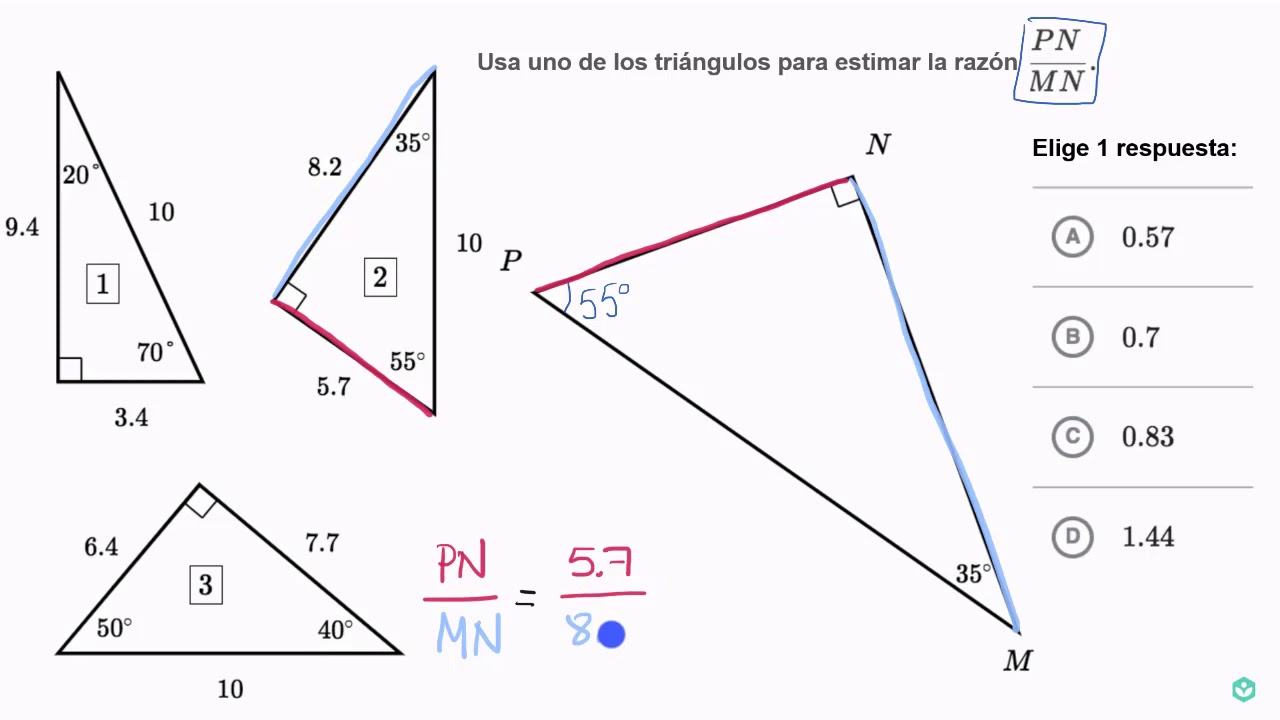
Usar semejanza para estimar la razón entre las longitudes de los lados
5.0 / 5 (0 votes)
