Circumference and area of a circle - exact answers in terms of pi
Summary
TLDRThis video explains how to calculate the exact circumference and area of a circle using pi, without approximations. It highlights that pi is an irrational number with an infinite decimal expansion, so for exact answers, pi should be used symbolically. The process demonstrates finding the circumference using the formula pi times the diameter and the area with pi times the radius squared. By substituting the radius of 9 meters, the results are expressed as 18π meters for the circumference and 81π square meters for the area, emphasizing that these are exact values in terms of pi.
Takeaways
- 🔢 The problem asks to find the circumference and area of a circle, with answers given in exact terms.
- 🔄 Typically, pi is approximated as 3.14 or with more digits, but pi is an irrational number, meaning it never ends.
- 🔠 To express exact answers, the symbol pi is used instead of an approximation.
- 📏 The formula for circumference is pi times the diameter of the circle.
- ⚪ In this example, the circle has a radius of 9 meters, meaning the diameter is 18 meters.
- 📝 The exact circumference is 18 pi meters, with the pi symbol left in place.
- 🏁 This format of writing 18 pi is just a convention, but it means 18 multiplied by pi.
- 🧮 The formula for area is pi times the radius squared.
- 💡 With a radius of 9 meters, the area becomes pi times 9 squared, which equals 81 pi meters squared.
- 🎯 The final answers for both circumference and area are given in exact terms using pi, which can be approximated later if needed.
Q & A
What does it mean to express a problem 'in terms of pi'?
-Expressing a problem 'in terms of pi' means leaving the symbol pi in the answer rather than using an approximation like 3.14. This gives an exact result instead of an approximate one.
Why do we avoid using an exact numerical value for pi?
-We avoid using an exact numerical value for pi because pi is an irrational number, meaning its decimal representation goes on forever without repeating. Using a symbol instead of a number allows for an exact result.
What is the formula for the circumference of a circle?
-The formula for the circumference of a circle is pi times the diameter.
In the example provided, what is the diameter of the circle?
-In the example, the diameter of the circle is 18 meters, since the radius is 9 meters and the diameter is double the radius.
How do you express the exact circumference of the circle in the example?
-The exact circumference is expressed as 18 pi meters, where 18 is the diameter and pi is left as a symbol for exactness.
What is the formula for the area of a circle?
-The formula for the area of a circle is pi times the radius squared.
How do you calculate the area of the circle in the example?
-To calculate the area, you square the radius (9), which gives 81, and then multiply by pi. The exact area is 81 pi square meters.
Why is the symbol pi placed second in the answers (e.g., 18 pi instead of pi 18)?
-The symbol pi is placed second as a convention in mathematical notation, similar to how you would write 18x instead of x18.
How would you find an approximate answer for the circumference or area?
-To find an approximate answer, you could replace pi with a numerical value like 3.14 and then perform the calculation.
What are the units for the exact circumference and area in the example?
-The exact circumference is measured in meters (18 pi meters), and the area is measured in square meters (81 pi square meters).
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
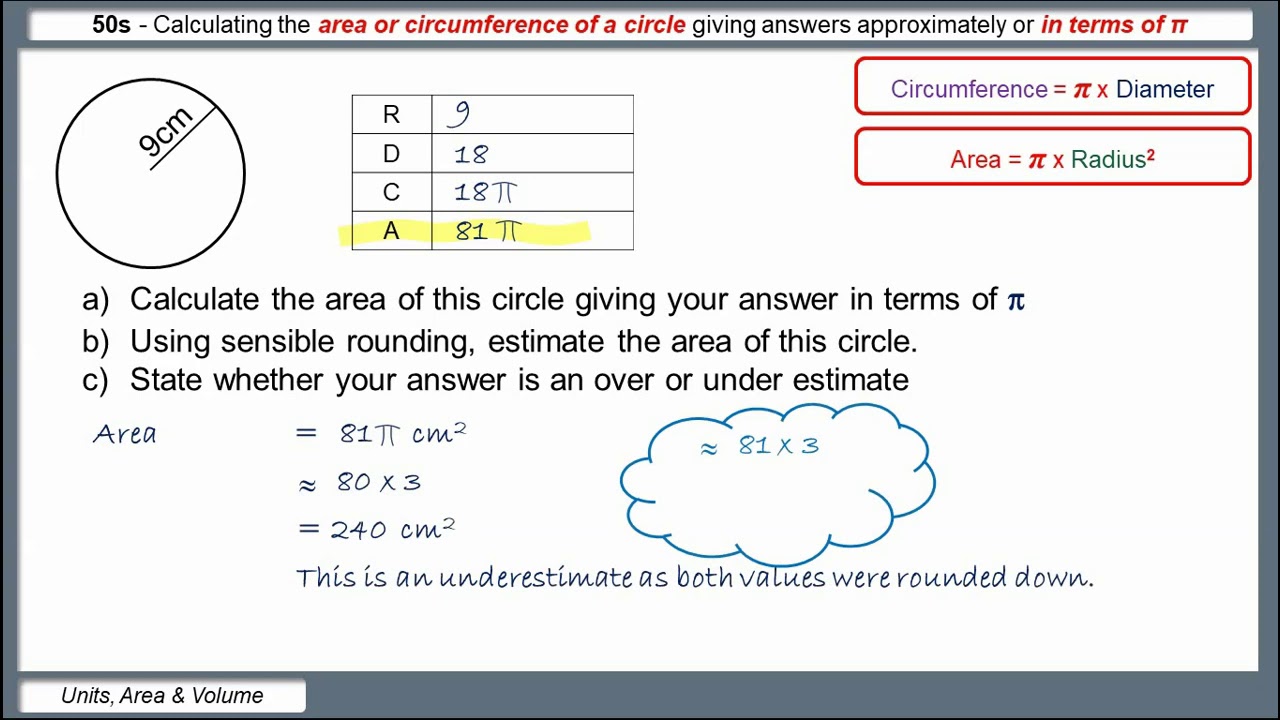
50s - Calculating area or circumference
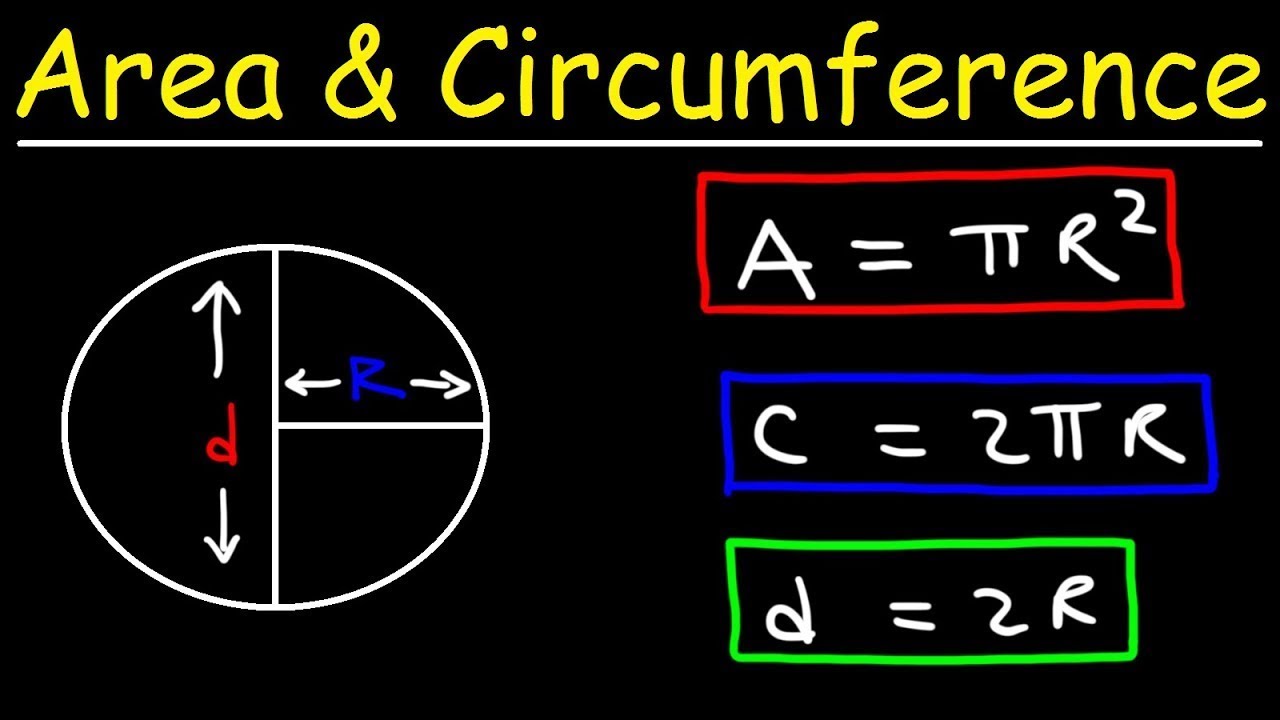
Circles - Area, Circumference, Radius & Diameter Explained!

Cara Mencari Keliling dan Luas Lingkaran Jika Jari-jari dan Diameter Diketahui

Circunferência - Raio, Diâmetro, Cálculo do Pi, Arco, Corda, Tangência | Matemática do ENEM

Comprimento da circunferência e o número pi

Cara Menghitung LUAS dan KELILING Lingkaran
5.0 / 5 (0 votes)
