Circunferência - Raio, Diâmetro, Cálculo do Pi, Arco, Corda, Tangência | Matemática do ENEM
Summary
TLDRIn this video, the concept of a circle and its elements, such as the circumference, radius, diameter, and pi (π), are explained. The difference between the circumference (the perimeter) and the circle (the enclosed area) is clarified. The video also discusses how to construct a circle, with an emphasis on the geometric properties of equidistant points. Furthermore, a practical Enem exam question about pipes is solved, using these principles to calculate the radius of a larger pipe. The video combines theoretical explanations with a real-world problem, making geometry engaging and accessible.
Takeaways
- 😀 Circumference refers to the perimeter or outer boundary of a circle, not the entire region inside it.
- 😀 The circle is the region inside the circumference, which includes all the points bounded by the circle's perimeter.
- 😀 A circle's key element is the radius (r), which is the distance from the center to any point on the circumference.
- 😀 The diameter (D) of a circle is twice the radius (2r), representing the distance across the circle through its center.
- 😀 Pi (π) is the constant ratio of the circumference to the diameter of a circle, approximately 3.14, and is used in the formula C = πD or C = 2πr.
- 😀 The number pi (π) can be estimated by dividing the circumference of any circular object by its diameter.
- 😀 An arc of a circle is a segment of the circumference, and it can represent any portion of the circle's perimeter.
- 😀 A semicircle is an arc that measures 180°, representing half of the circumference.
- 😀 A chord is a line segment connecting any two points on the circumference, and it doesn't pass through the center of the circle.
- 😀 Two circles are tangent if they touch at exactly one point, and this point is called the point of tangency.
- 😀 The video includes a practical exercise based on an ENEM exam question, which demonstrates how to solve a real-world geometry problem involving multiple circles.
Q & A
What is the difference between a circumference and a circle?
-A circumference refers to the perimeter or the boundary of the figure, whereas a circle includes the entire area enclosed by the circumference. The circle is the region inside, and the circumference is just the boundary.
What defines the construction of a circumference?
-A circumference is constructed by selecting a center point and drawing a set of points that are equidistant from the center. The distance from the center to these points is called the radius, denoted as 'R'.
How is the diameter of a circumference defined?
-The diameter of a circumference is twice the radius. It is the distance between two points on the circumference that pass through the center, and it is denoted as 'D'.
What mathematical constant is used in the formula for the circumference?
-The mathematical constant used is pi (π), which is the ratio between the circumference and the diameter. Its approximate value is 3.14.
How can we approximate the value of pi using real-world objects?
-To approximate pi, you can measure the circumference of a circular object, such as a coin or plate, using a string. Then, measure the diameter and divide the circumference by the diameter. The result will be approximately 3.14.
What is an arc in a circle?
-An arc is a segment of the circumference. It represents a portion of the circular boundary, which can vary in length depending on the angle of the segment.
What is a semicircle, and how is it formed?
-A semicircle is an arc that spans half of a circle, corresponding to a 180-degree angle. It is formed by dividing a circle along its diameter.
What is a chord in the context of a circle?
-A chord is a straight line segment that connects two points on the circumference of the circle. Unlike the diameter, it does not necessarily pass through the center.
What are tangent circles, and how do they interact?
-Tangential circles are two circles that touch each other at exactly one point. This point of contact is known as the point of tangency.
How does the ENEM 2013 question relate to the geometrical concepts discussed?
-The ENEM 2013 question involves a practical application of the concepts of radius, distance between circles, and tangency. It uses a system of pipes arranged with certain distances to find the radius of a larger pipe, applying the understanding of circles, tangents, and geometric properties.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

50s - Calculating area or circumference

Circles: radius, diameter, circumference and Pi | Geometry | Khan Academy

Radius & diameter from circumference | High School Geometry | High School Math | Khan Academy

Comprimento da circunferência e o número pi
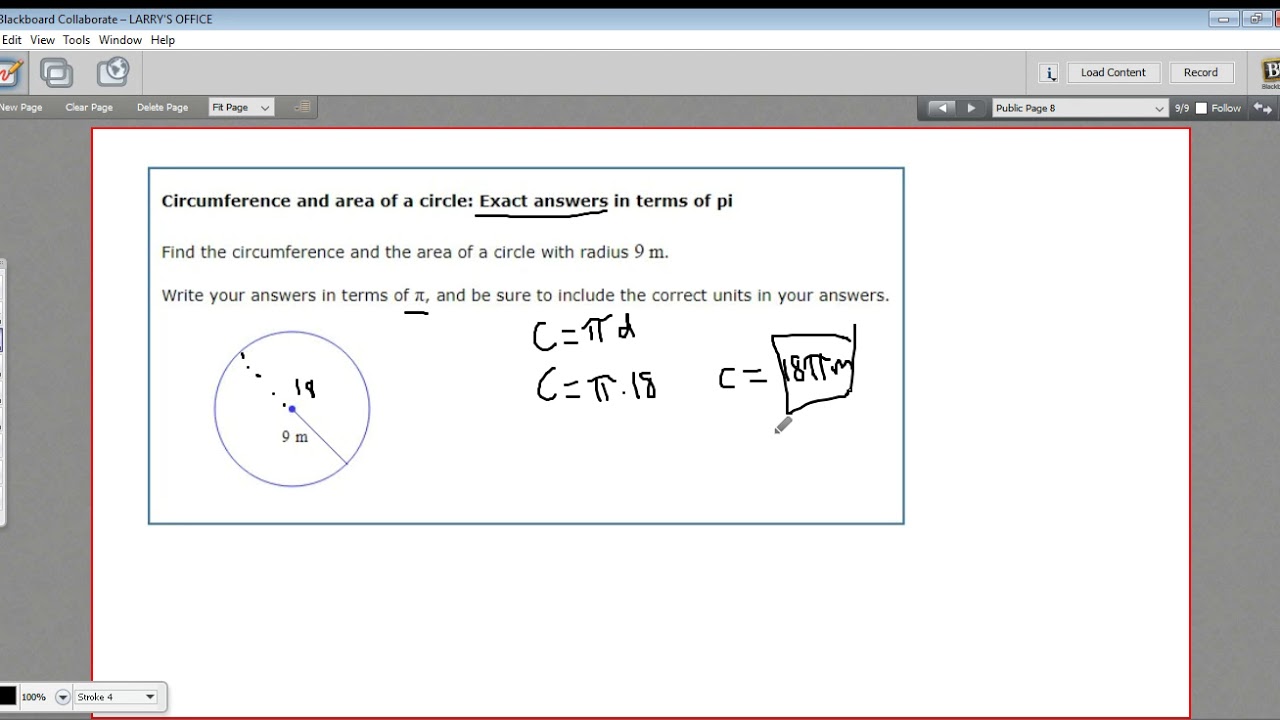
Circumference and area of a circle - exact answers in terms of pi
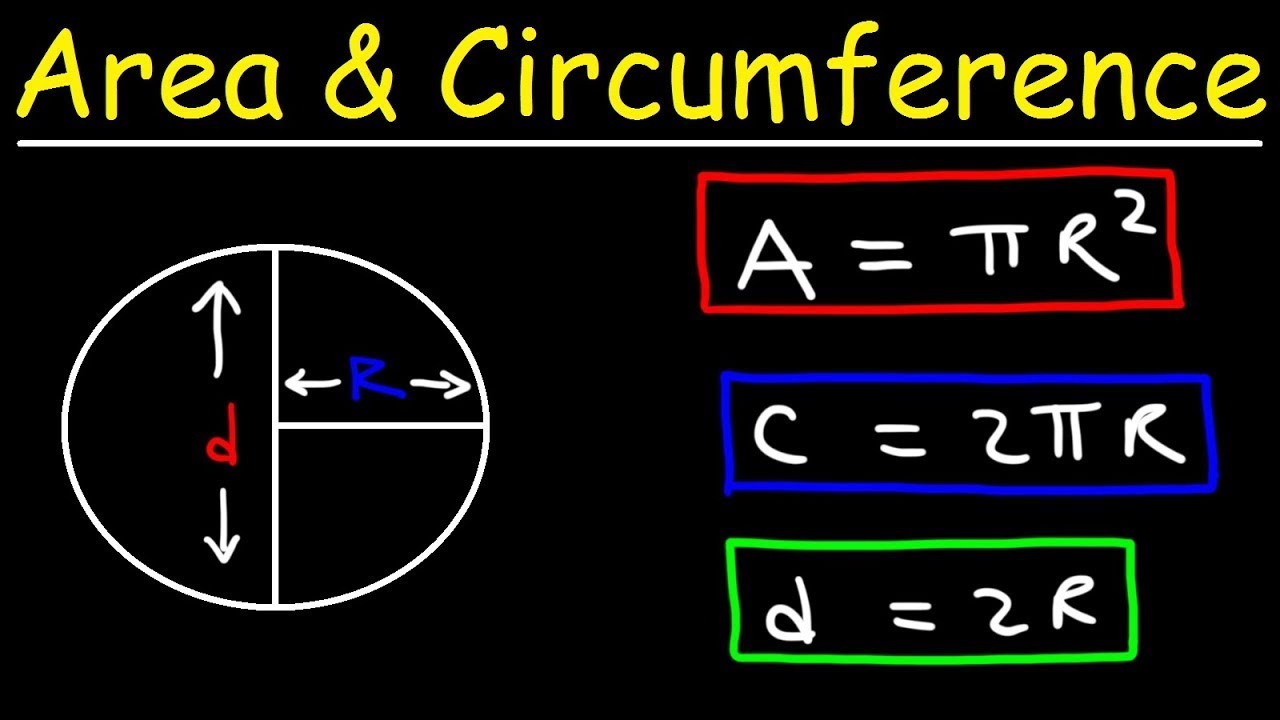
Circles - Area, Circumference, Radius & Diameter Explained!
5.0 / 5 (0 votes)