DISTRIBUCIÓN NORMAL desde CERO | 2º bachillerato
Summary
TLDREste video ofrece una explicación básica sobre la distribución normal y el cálculo de probabilidades, ideal para quienes buscan comprender sus conceptos fundamentales. Comienza describiendo variables continuas, distribuciones teóricas y empíricas, y las propiedades esenciales de la función de densidad de probabilidad. El enfoque se centra en la curva de Gauss, sus parámetros clave (media y desviación típica), y cómo simplificar los cálculos usando la normal estándar (media 0, desviación 1). También se enseña a usar tablas para determinar probabilidades, explicando paso a paso cómo tipificar variables con ejemplos prácticos.
Takeaways
- 📊 La distribución normal es una representación común de variables continuas en estadísticas.
- 📈 Se define a través de una función de densidad de probabilidad, que cumple con dos condiciones fundamentales.
- 🔢 La probabilidad de eventos puntuales en una distribución continua es cero, ya que se representa por áreas bajo la curva.
- 📚 La distribución normal se caracteriza por su media (centro de gravedad) y desviación típica (medida de dispersión).
- 🎓 La distribución normal fue descubierta por el matemático alemán Carl Friedrich Gauss, y también se conoce como curva de error.
- 📉 La función de densidad de probabilidad de una distribución normal tiene la forma de una campana, simétrica respecto a la media.
- 🌐 Aunque existen muchas distribuciones normales con diferentes medias y desviaciones típicas, todas son esencialmente similares y se pueden 'tipificar'.
- 🔄 La 'tipificación' de una variable normaliza la distribución a una media de 0 y una desviación típica de 1, facilitando el uso de tablas estandarizadas.
- 📖 Las tablas de probabilidades normales proporcionan la probabilidad de que la variable sea menor o igual que un cierto valor, y son esenciales para el cálculo de probabilidades.
- 🔢 Para calcular probabilidades en una distribución normal dada, se realiza una 'tipificación' de la variable y se consulta en las tablas correspondientes.
Q & A
¿Qué es una distribución de probabilidad de variable continua?
-Una distribución de probabilidad de variable continua es una idealización de una distribución estadística que se obtiene de manera empírica (mediante observación o experimentación) o teórica, y permite representar variables que pueden tomar infinitos valores.
¿Cuáles son los ejemplos típicos de variables continuas?
-Algunos ejemplos típicos de variables continuas son estaturas, pesos y tiempos, ya que estas variables pueden tomar un rango infinito de valores dentro de un intervalo determinado.
¿Cuáles son las dos condiciones que debe cumplir una función de densidad de probabilidad?
-1. La función debe ser mayor o igual a cero (no negativa). 2. El área bajo la curva de la función de densidad de probabilidad debe ser igual a 1, ya que esto representa la probabilidad total.
¿Cómo se calcula la probabilidad de que una variable esté dentro de un intervalo?
-Para calcular la probabilidad de que una variable esté dentro de un intervalo, se debe obtener el área bajo la curva de la función de densidad en ese intervalo, lo que se realiza mediante una integral definida.
¿Por qué la distribución normal se llama también 'curva de error'?
-La distribución normal se llama 'curva de error' porque Gauss, su descubridor, la desarrolló estudiando los errores cometidos al medir ciertas magnitudes. La mayoría de los valores se concentran alrededor de la media, y los errores más pequeños son más probables que los grandes.
¿Qué representa gráficamente la distribución normal?
-La representación gráfica de la distribución normal tiene forma de campana, mostrando que la mayoría de los valores de la distribución se concentran alrededor de la media y disminuyen simétricamente a medida que se alejan de ella.
¿Por qué no es posible calcular la integral de la función de densidad de la distribución normal directamente?
-La integral de la función de densidad de probabilidad de la distribución normal no tiene una primitiva conocida, por lo que no se puede calcular directamente. En su lugar, se usan tablas de probabilidades obtenidas mediante métodos numéricos.
¿Cómo se simplifica el cálculo de probabilidades para una distribución normal?
-Para simplificar el cálculo, se utiliza la distribución normal estándar con media 0 y desviación típica 1. Para convertir una distribución normal a esta forma estándar, se 'tipifica' la variable restando la media y dividiendo por la desviación típica.
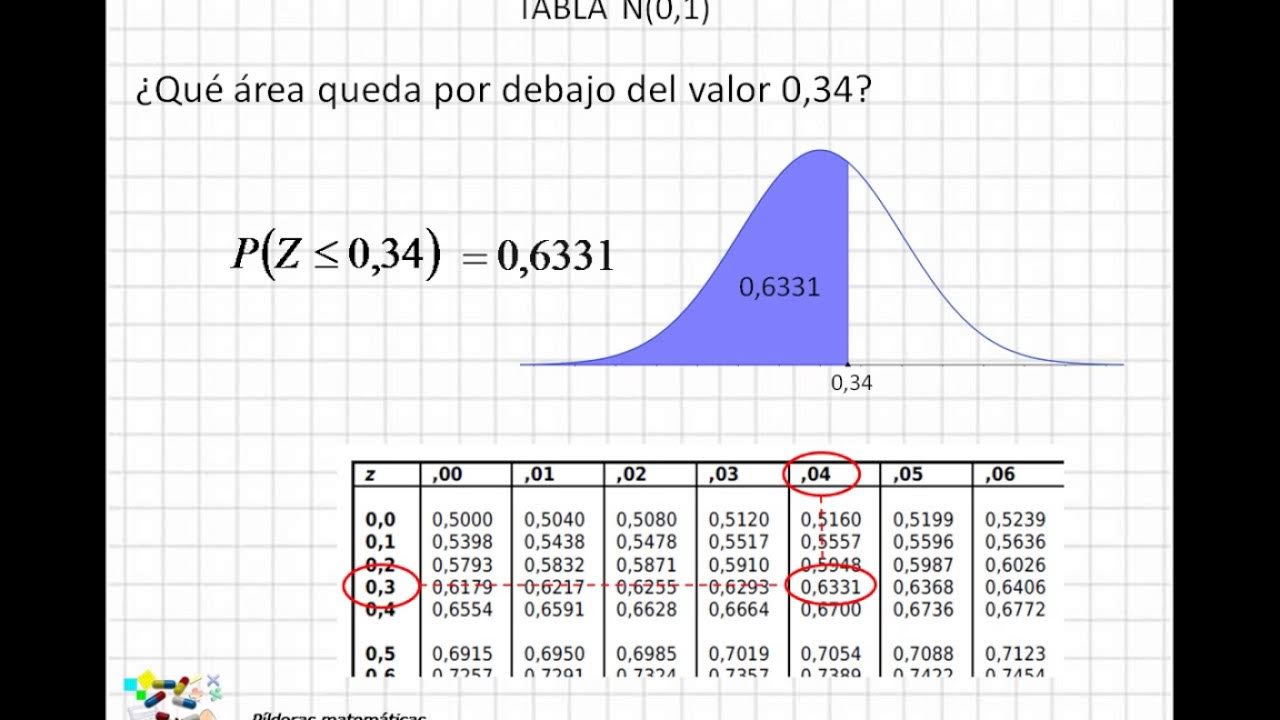
¿Cómo se usa la tabla de probabilidades para calcular probabilidades con la distribución normal estándar?
-Se busca el valor correspondiente en la tabla de probabilidades estándar, que muestra la probabilidad de que la variable sea menor o igual a un número positivo. Por ejemplo, si se tiene un valor z = 0.75, se busca en la tabla para encontrar su probabilidad asociada.
¿Qué se hace cuando el valor de z es negativo al usar la tabla de probabilidades?
-Si el valor de z es negativo, se puede usar la simetría de la distribución normal. La probabilidad de un valor negativo se transforma en una probabilidad positiva usando el suceso contrario, es decir, la probabilidad de que z sea menor o igual que el valor negativo es igual a 1 menos la probabilidad de que z sea mayor o igual que el valor positivo correspondiente.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
04 Cómo usar la tabla de distribución normal
Tabla de probabilidades de la Distribucion Normal Estandar - Valores z

2.8.a) Razones de Cambio en Ciencias Naturales y Sociales. Definición y ejemplo

✅RADIACIÓN ELECTROMAGNÉTICA en ONDAS | EJEMPLO PASO a PASO| QUÍMICA

¿Qué es la Distribución Normal? | Videos Educativos Aula365

Función de probabilidad de variable aleatoria discreta | Intro
5.0 / 5 (0 votes)
