Fluid Mechanics Lesson 02F: Manometers
Summary
TLDRIn this educational video, the presenter explores the function and operation of a manometer, a device used to measure pressure differences. They conduct a hands-on demonstration with a U-tube manometer, explaining how blowing or sucking into it creates a height difference in the fluid. The video delves into hydrostatic equations, illustrating how to calculate gauge pressure and absolute pressure using manometers filled with various fluids. It also addresses the impact of fluid densities and manometer design on pressure readings, offering practical tips for accurate measurements and emphasizing the importance of not simplifying equations when densities are significantly different.
Takeaways
- 🔍 The purpose of a manometer is to measure unknown pressure or pressure differences.
- 💧 Manometers can be filled with any fluid and can be of any shape.
- 📐 The key equation used for analyzing manometers is the hydrostatic pressure equation, ΔP = ρ g h.
- 🌀 A YouTube manometer demonstration shows that blowing or sucking into a tube can create a height difference in the fluid.
- 🌡 When calculating gauge pressure, one side of the manometer is open to the atmosphere.
- 📉 In a U-tube manometer, the manometer fluid must be denser than the fluid being measured to stay at the bottom.
- 🔄 The process of solving manometer problems involves selecting a reference point and moving around the tube, accounting for pressure changes when moving up or down.
- ⚖️ The height difference in a manometer (delta z) does not depend on the diameter or length of the U-tube, as long as capillary effects are negligible.
- 📏 Inclined manometers offer better resolution because they have more tick marks per unit of height compared to vertical ones.
- 📋 The vertical location of the manometer can affect the elevation difference if the fluid above the manometer is not air.
- 🚫 It's advised not to make approximations when the fluid being measured is a liquid, as the effect can be significant and lead to errors.
Q & A
What is the primary purpose of a manometer?
-The primary purpose of a manometer is to measure an unknown pressure or a pressure difference.
What is the key equation used for hydrostatics in the context of manometers?
-The key equation used for hydrostatics in manometers is the workhorse equation for hydrostatics, which is delta p = rho * g * h.
How does a U-tube manometer demonstrate pressure changes when blowing or sucking into a tube?
-A U-tube manometer demonstrates pressure changes by showing a height difference between the left and right legs of the manometer when blowing or sucking into a tube, which corresponds to the gauge pressure.
What is the significance of the height difference observed in the manometer when the professor blows or sucks into the tube?
-The height difference observed in the manometer when blowing or sucking into the tube signifies the gauge pressure in the mouth, which is the difference in pressure between the atmosphere and the mouth.
Why does the manometer fluid have to be denser than the fluid being measured?
-The manometer fluid has to be denser than the fluid being measured to ensure that the manometer fluid stays at the bottom of the U-tube and provides an accurate pressure reading.
What is the significance of the points labeled 1, 1', and 2 in the manometer analysis?
-The points labeled 1, 1', and 2 are used to apply the hydrostatic equation to calculate the absolute and gauge pressures in the manometer. These points represent different pressure levels within the manometer system.
Why is it important to consider the direction of fluid movement (up or down) when applying the hydrostatic equation?
-The direction of fluid movement is important because it determines whether to add or subtract pressure in the hydrostatic equation. Going down increases pressure (add), while going up decreases pressure (subtract).
What is the general formula derived for calculating the pressure difference in a manometer?
-The general formula derived for calculating the pressure difference in a manometer is delta p = (rho_m - rho_a) * g * (z2 - z1) - rho_a * g * (za - z2), where rho represents fluid density, g is the acceleration due to gravity, and z represents elevation.
Why is it advised to not simplify the equation by neglecting rho_a when rho_a is very small compared to rho_m?
-It is advised not to simplify the equation by neglecting rho_a because even if rho_a is small, it can become significant in certain situations, and neglecting it could lead to errors in pressure calculations.
How does the shape of the U-tube manometer affect the elevation difference (delta z)?
-The shape of the U-tube manometer does not affect the elevation difference (delta z) as long as the tube diameter is large enough to neglect capillary effects and the tube is long enough to include the delta z.
What is the advantage of an inclined manometer over a vertical one?
-An inclined manometer has the advantage of better resolution because it allows for more tick marks per centimeter, providing a more precise measurement of the height difference.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

4.3d Measuring Pressure: Manometer 'U Tubes' and Barometer Pipes | AS | Cambridge A Level Physics

Fluida Dinamis • Part 4: Venturimeter / Pipa Venturi

01 - Fluid Transport - Pitot Tube

Endotracheal Tube Care
Mekanika Fluida FM01 (Lecture3: 6/8). Venturimeter - Aplikasi persamaan Bernoulli
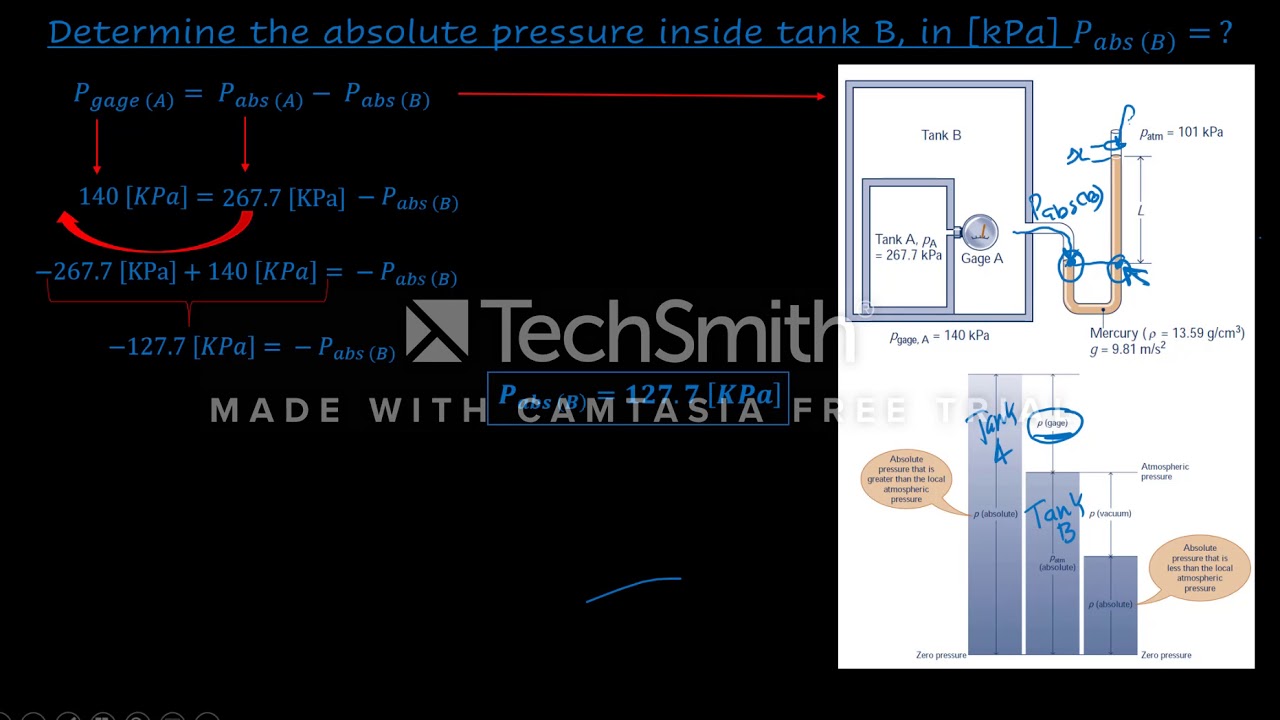
Solving problem related to absolute, atmospheric, gage pressures and The U-tube manometer.
5.0 / 5 (0 votes)
