Probability of an Event
Summary
TLDRThis script delves into the concept of probability, distinguishing between impossible and certain events with probabilities of zero and one, respectively. It introduces the idea of a sample space and defines an event as a set of simple outcomes. The script contrasts experiments with equally-likely outcomes, like tossing a fair coin, with those that are not, like the chance of an accident. It also highlights the difference between classical experiments, which assume equal likelihood, and real-life scenarios that often do not. Two approaches to calculating probability are presented: the classical method for equally-likely outcomes and the empirical method for others, emphasizing the importance of understanding both for accurate probability assessment.
Takeaways
- 🔢 The probability of an impossible event is 0, and the probability of a certain event is 1.
- 🎰 Probabilities of other events must fall between 0 and 1.
- 🧩 To find the probability of an event, consider the experiment's sample space, which includes all possible outcomes.
- 🪙 When tossing a fair coin, heads and tails are equally likely outcomes.
- 🚗 The likelihood of an accident while driving to work is not necessarily equal to not having an accident.
- 🎲 Rolling a die has six equally likely outcomes, assuming the die is fair.
- 💳 The number of credit cards in a person's wallet is not equally likely across all possible counts.
- 🎯 Classical probability applies to experiments with equally likely outcomes.
- 🌐 Empirical probability is used when outcomes are not equally likely, reflecting real-world scenarios.
- 📊 Two approaches to finding probabilities are classical and empirical, chosen based on the nature of the experiment's outcomes.
Q & A
What is the range of probability for any given event?
-The probability of any given event must be between zero and one, where zero represents an impossible event and one represents a certain event.
What is a sample space in the context of probability?
-A sample space is the set of all possible simple outcomes for a given experiment that can be used to define an event.
What is the difference between tossing a coin and driving to work in terms of probability?
-Tossing a coin is an experiment with equally-likely outcomes (heads or tails), whereas driving to work does not have equally-likely outcomes when considering the chance of an accident.
Why are the outcomes of tossing a fair coin considered equally likely?
-There is no reason to believe that the chances of getting heads are different from getting tails when tossing a fair coin.
How does the probability of getting in an accident while driving to work differ from the probability of getting heads or tails when tossing a coin?
-The probability of getting in an accident is not equally likely compared to not getting in an accident, unlike the equal chances of heads or tails when tossing a coin.
What is the difference between rolling a die and counting credit cards in a wallet in terms of probability outcomes?
-Rolling a die has equally-likely outcomes for each number between one and six, while the number of credit cards in a wallet does not have equally-likely outcomes across all possible counts.
Why are the outcomes of rolling a fair die considered equally likely?
-There is no reason to believe that any number between one and six is more or less likely than any other number when rolling a fair die.
What is the classical approach to finding the probability of an event?
-The classical approach is used when an experiment has equally-likely simple outcomes, and it involves calculating the probability by dividing the number of favorable outcomes by the total number of possible outcomes.
What is the empirical approach to finding the probability of an event?
-The empirical approach is used when an experiment does not have equally-likely simple outcomes, and it involves estimating the probability based on observed frequencies or data.
Why is it important to be able to work with both classical and empirical experiments?
-It is important because most classical experiments have equally-likely outcomes, but in real life, most experiments do not, and understanding both approaches allows for accurate probability calculations in various scenarios.
How do you determine which approach to use when calculating the probability of an event?
-You use the classical approach if the experiment has equally-likely simple outcomes, and the empirical approach if the outcomes are not equally likely.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
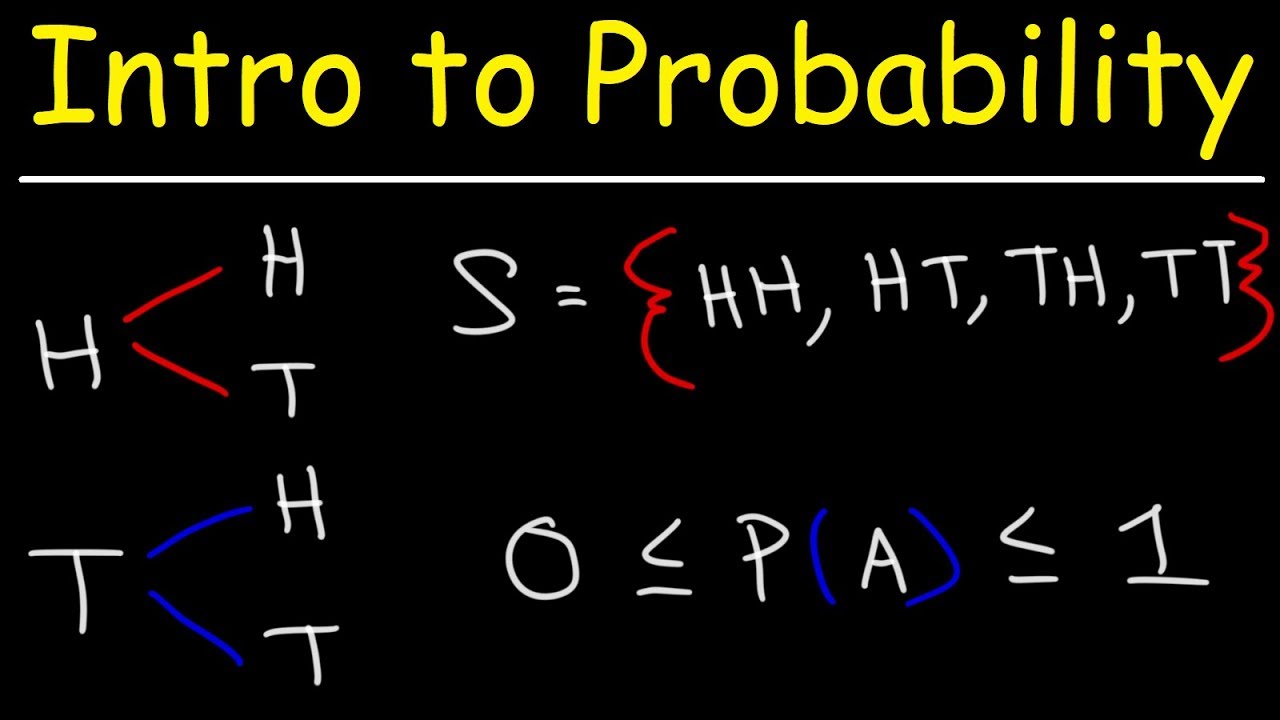
Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams

Math Antics - Basic Probability

The Classical Approach

Axioms of Probability - Probability and Statistics | Engineering Mathematics | GATE CSE

Probability Part 1: Rules and Patterns: Crash Course Statistics #13
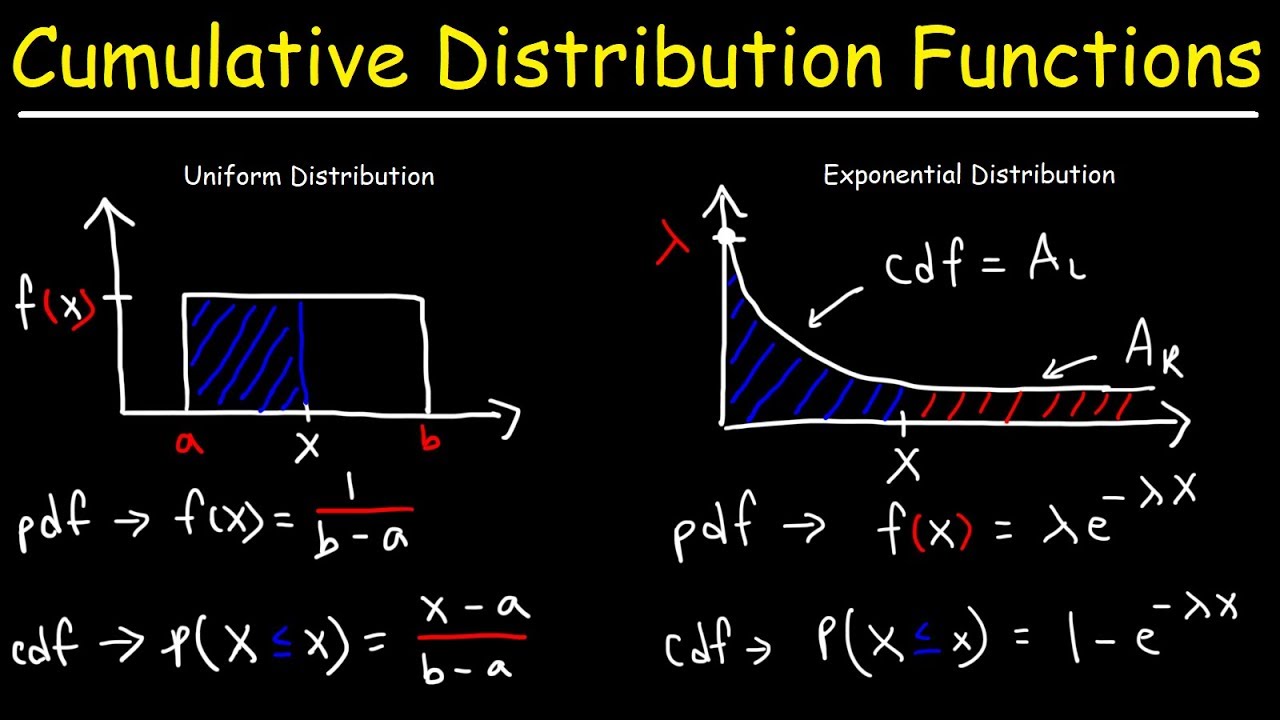
Cumulative Distribution Functions and Probability Density Functions
5.0 / 5 (0 votes)
