QUÉ ES UNA FUNCIÓN, Sobreyectiva, inyectiva, biyectiva
Summary
TLDREl guion trata sobre las funciones matemáticas, explicando que son relaciones entre conjuntos donde cada elemento del primer conjunto está asociado con un único elemento del segundo. Se ilustra con ejemplos cómo algunas relaciones no son funciones debido a que un elemento puede estar relacionado con más de uno del segundo conjunto. Además, se discuten las clases de funciones: sobreyectivas (algunos elementos del segundo conjunto no están asociados con ninguno del primero), inyectivas (cada elemento del segundo conjunto está asociado con exactamente uno del primero) y biyectivas (combinación de sobreyectiva e inyectiva). El video utiliza analogías como estudiantes y sillas para explicar conceptos, destacando la importancia de entender funciones en contextos naturales y científicos.
Takeaways
- 😀 Una función es una relación donde cada elemento de un conjunto está asociado con un único elemento de otro conjunto.
- 🔍 Incluso si hay elementos en el segundo conjunto que no están asociados con ningún elemento del primer conjunto, la relación sigue siendo una función.
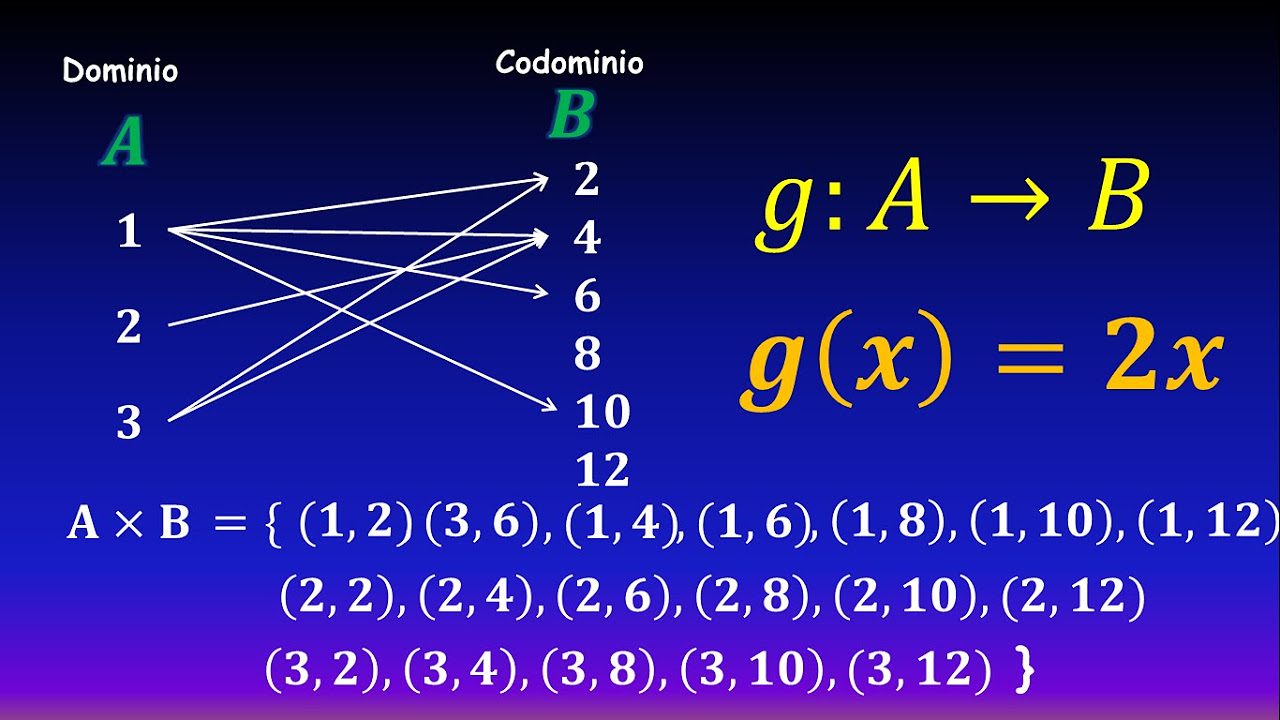
- 🚫 Si un elemento del primer conjunto está asociado con más de un elemento en el segundo conjunto, entonces la relación no es una función.
- 📚 Se presentan cuatro clases de funciones, cada una definida por cómo los elementos de los conjuntos están asociados entre sí.
- 👀 En una función sobreyectiva, hay elementos en el segundo conjunto que no están asociados con ningún elemento del primer conjunto.
- 🔄 Las funciones sobreyectivas y sobrelectivas son aquellas donde todos los elementos del segundo conjunto están asociados con al menos un elemento del primer conjunto.
- 💉 Las funciones inyectivas son aquellas donde a cada elemento del segundo conjunto le llega exactamente un elemento del primer conjunto.
- 💼 Se utiliza la analogía de estudiantes y sillas para ilustrar las diferentes clases de funciones, destacando la importancia de que cada elemento del segundo conjunto esté asociado con un único elemento del primero.
- 🌐 Se enfatiza la relevancia de las funciones en la naturaleza y la ciencia, donde muchos fenómenos pueden ser modelizados y explicados mediante funciones.
- 📢 El video invita a los espectadores a participar en la discusión, dejando comentarios y preguntas en la sección de comentarios.
Q & A
¿Qué es una función en matemáticas?
-Una función es una relación entre dos conjuntos donde a cada elemento del primer conjunto le corresponde un elemento y sólo un elemento del segundo conjunto.
¿Qué sucede si a algunos elementos del primer conjunto no les corresponde ningún elemento en el segundo conjunto?
-A pesar de que algunos elementos no tienen correspondencia, la relación entre los conjuntos sigue siendo una función.
¿Por qué no es una función si un elemento del primer conjunto corresponde a dos elementos distintos del segundo conjunto?
-Porque en una función, un elemento del primer conjunto solo puede corresponder a un solo elemento del segundo conjunto, no a múltiples.
¿Cuáles son los cuatro tipos de relaciones entre conjuntos mencionados en el guion?
-Las cuatro relaciones son: función, función no sobreyectiva, función sobreyectiva y función biyectiva.
¿Qué es una función sobreyectiva?
-Una función sobreyectiva es aquella en la que todos los elementos del segundo conjunto están relacionados con elementos del primer conjunto.
¿Qué característica tienen las funciones inyectivas?
-Las funciones inyectivas son aquellas donde a cada elemento del segundo conjunto le llega únicamente un elemento del primer conjunto.
¿Qué es una función biyectiva?
-Una función biyectiva es aquella que es a la vez inyectiva y sobreyectiva, es decir, donde hay una correspondencia única y total entre los elementos de ambos conjuntos.
¿Cómo se relaciona la función biyectiva con la situación de los estudiantes y las sillas?
-Una función biyectiva en este contexto sería una relación donde cada estudiante tiene su silla asignada de manera única y no hay sillas sobrantes ni faltantes.
¿Por qué es importante estudiar las funciones en la naturaleza?
-Es importante porque casi todas las relaciones en la naturaleza pueden ser modelizadas y explicadas mediante funciones, lo que es fundamental en campos como la física y la biología.
¿Cómo se puede aplicar el concepto de función en un entorno educativo según el guion?
-Se puede aplicar al asignar estudiantes a sillas de manera que cada estudiante tenga su propia silla, simbolizando una función biyectiva perfecta.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)