Curso de Integrales. Capítulo 2: la constante, el símbolo y el diferencial. Una propuesta didáctica.
Summary
TLDREl guion del video ofrece una introducción amigable al concepto de integral, comparando el aprendizaje de la integral con aprender a hablar, donde primero se adquiere la idea básica antes de abordar el rigor matemático. Expone la importancia de la 'c' en las integrales como constante de integración, y cómo representa el desplazamiento en el eje y cuando x es cero. Además, se discuten las fórmulas para dividir potencias con la misma base, la derivación de potencias y la importancia de la constante en la derivada de una función. El guion también explora el símbolo de la integral y su significado en el contexto de áreas y sumas infinitas, concluyendo con cómo insertar integrales en una aplicación de procesamiento de texto.
Takeaways
- 📚 El concepto de integral se acerca primero de forma amigable y sin rigor, similar a cómo se aprende a hablar, para facilitar su comprensión.
- 🔍 Se utiliza el área para introducir la idea de integral, como un modelo didáctico que ayuda a enraizar la idea de manera sencilla.
- 🧩 Aprender la integral sin sobrecargar la carga de trabajo cerebral es importante, al igual que aprender a manejar un coche paso a paso.
- 📉 El proceso de aprendizaje de la integral comienza con una aproximación general y luego se va enfolando en detalles más específicos, como el tráfico y las señales en la conducción.
- ✍️ Al calcular integrales, se pone una 'c' al final, que representa la suma de una constante a la función antiderivada.
- 🔢 La 'c' en las integrales es como los gastos fijos en economía o cualquier otro valor que se añade al inicio cuando x=0.
- 📈 La gráfica de las funciones muestra cómo la 'c' es el desplazamiento vertical de la función con respecto al eje x.
- 🤔 La curiosidad sobre el origen del símbolo de la integral y su evolución desde las anotaciones de Newton hasta el símbolo actual.
- 📐 El símbolo de integral se usa para denotar el conjunto de primitivas que, al derivar, dan la función original.
- 📏 El 'dx' en una integral representa una pequeña diferencia en el eje x, la base de un rectángulo en el proceso de sumar áreas.
- 📝 La integral de una función se escribe formalmente como la suma de rectángulos con altura 'f(x)' y base 'dx', y se puede insertar en aplicaciones de edición de texto como Word.
Q & A
¿Qué es el concepto de integral y cómo se acerca al mismo el guion?
-El concepto de integral se acerca a través de la idea de área, utilizando un modelo didáctico amigable que no requiere rigor inicialmente, permitiendo que el entendimiento se asienta antes de abordar el tema con rigurosidad matemática.
¿Por qué se menciona la importancia de entender el concepto de integral antes de abordarlo con rigor?
-La comprensión del concepto de integral sin rigor sirve como base para poder enfrentarlo con rigurosidad más adelante, evitando la sobrecarga cognitiva que puede causar el aprendizaje de conceptos complejos de forma abrupta.
¿Cómo se relaciona el aprendizaje de la integral con el aprendizaje del lenguaje o el manejo de un coche?
-Se compara el aprendizaje de la integral con el aprendizaje del lenguaje o el manejo de un coche, enfatizando la importancia de comenzar con un enfoque más amplio y luego pasar a detalles específicos y automáticos.
¿Qué es la 'c' que se menciona al final de calcular una integral y por qué se pone?
-La 'c' representa una constante que se añade al final de una integral para representar el conjunto de antiderivadas o primitivas de la función, ya que una misma derivada puede corresponder a diferentes funciones.
¿Qué es la derivada y cómo se calcula la derivada de una función simple como x?
-La derivada es una medida de la pendiente de una función en un punto dado. La derivada de x es 1, ya que la pendiente de la función f(x) = x en cualquier punto es 1.
¿Por qué las funciones x - 1, x + 1 y x tienen la misma derivada?
-Tienen la misma derivada porque la derivada es la pendiente y todas estas funciones tienen una pendiente de 1 en cualquier punto del eje x.
¿Qué significa el símbolo 'dx' en una integral y cómo se relaciona con el concepto de área?
-El 'dx' en una integral representa una pequeña diferencia en el eje x, y es parte del proceso de sumar áreas de rectángulos con bases muy pequeñas para calcular el área bajo la curva de una función.
¿Cómo se puede representar formalmente la integral de una función en una ecuación?
-La integral de una función se representa formalmente como ∫f(x)dx, donde 'f(x)' es la función y 'dx' indica la diferencia infinitesimal en el eje x.
¿Qué es el símbolo 'S' que se coloca delante de una integral y qué representa?
-El símbolo 'S', que en realidad es el símbolo de integral ∫, se coloca delante de una función para indicar que se está calculando el conjunto de primitivas de esa función.
¿Cómo se inserta una integral en una aplicación de procesamiento de texto como Word?
-Para insertar una integral en Word, se va a la pestaña 'Insertar', se selecciona 'Ecuación', se coloca el cursor donde se desea la integral, se elige el símbolo de integral y se escribe la función correspondiente, añadiendo 'dx' al final.
¿Qué es el significado de 'integral' fuera del contexto matemático y cómo se relaciona con otros contextos como la economía o la medicina?
-Fuera del contexto matemático, 'integral' puede referirse a algo esencial o fundamental en otros campos. Por ejemplo, en economía podría significar los gastos fijos de una empresa, mientras que en medicina podría tener otro significado específico relacionado con el campo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Introducción al cálculo integral | Khan Academy en Español

¿Qué es la derivada? El concepto gráfico de derivada. ¿Qué es doblegar la curva?

14. Integral de raiz quinta de 2x al cubo (Exponente fraccionario)
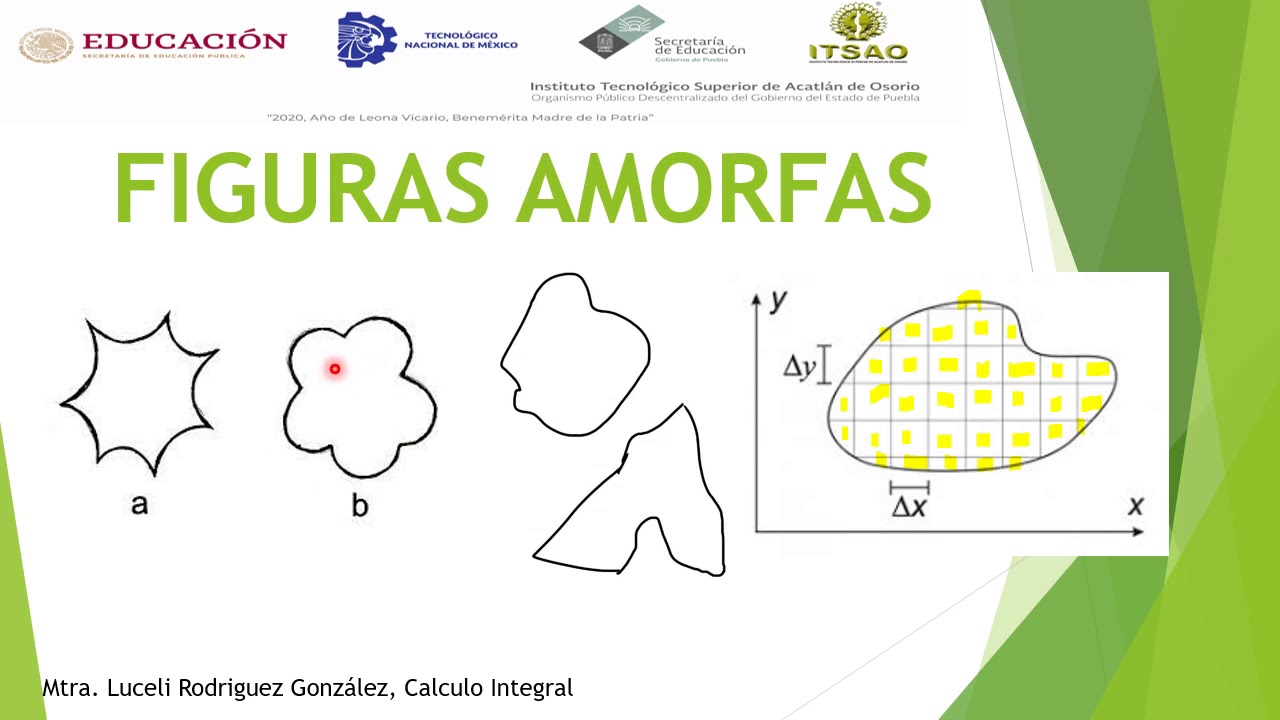
Figuras amorfas y notación sumatoria

Calculo integral

Ángulos en la circunferencia │ ángulo central
5.0 / 5 (0 votes)
