Ecuaciones diferenciales de variables separables | Introducción
Summary
TLDREn este video, el instructor explica cómo resolver ecuaciones diferenciales, enfocándose especialmente en las ecuaciones de variables separables. A lo largo del video, se abordan ejemplos prácticos que muestran cómo identificar y manipular las ecuaciones para separar las variables. El video también destaca la importancia de saber integrar para resolver este tipo de ecuaciones. Al final, se presenta un ejercicio para que los espectadores practiquen lo aprendido y se invita a profundizar en el tema a través de otros recursos disponibles.
Takeaways
- 😀 La ecuación diferencial que se presenta involucra términos que deben ser integrados para encontrar la solución.
- 😀 Es esencial entender cómo separar las variables en una ecuación diferencial para resolverla correctamente.
- 😀 El proceso de integración se utiliza para despejar términos y encontrar la solución de la ecuación.
- 😀 Las ecuaciones diferenciales pueden ser clasificadas según si son separables o no.
- 😀 Una ecuación diferencial separable permite que las variables se separen a ambos lados de la ecuación para facilitar la integración.
- 😀 En algunos casos, la derivada de la ecuación debe ser despejada antes de poder analizar si es separable.
- 😀 El despeje de la derivada implica mover términos y simplificar la ecuación antes de intentar separarla.
- 😀 Las ecuaciones que contienen multiplicaciones entre funciones de diferentes variables también pueden ser separables, dependiendo de su estructura.
- 😀 Es importante identificar cuándo las letras en una ecuación no pueden ser combinadas, ya que esto indica que no es una ecuación separable.
- 😀 Al final del video, se invita a los estudiantes a practicar con un ejercicio para reconocer ecuaciones separables y mejorar su comprensión del tema.
- 😀 La clase termina con una invitación a profundizar en el tema a través de un curso completo y otros recursos educativos.
Q & A
¿Qué es una ecuación diferencial separable?
-Una ecuación diferencial separable es aquella que se puede escribir de forma que todas las funciones de una variable se encuentren en un lado de la ecuación y las funciones de la otra variable en el otro lado, permitiendo así que se puedan integrar de forma directa.
¿Qué se necesita hacer para resolver una ecuación diferencial separable?
-Para resolver una ecuación diferencial separable, es necesario reorganizar la ecuación de forma que todas las variables estén separadas, es decir, las funciones de una variable se encuentren en un lado de la ecuación y las funciones de la otra en el lado opuesto. Luego, se integra ambos lados de la ecuación.
En el video, ¿cómo se explica que una ecuación no sea separable?
-En el video se menciona que una ecuación no es separable cuando no se puede despejar la derivada de manera que las funciones de una variable estén separadas. Por ejemplo, si en el denominador o numerador de la ecuación aparecen funciones con más de una variable, no se puede separar fácilmente.
¿Cuál es el primer paso cuando una ecuación diferencial no está separada?
-El primer paso es despejar la derivada para obtener una expresión en la que las funciones de las variables estén separadas. Esto puede implicar mover términos hacia un lado u operar con constantes y variables de manera apropiada.
¿Qué significa 'despejar la derivada' en el contexto de las ecuaciones diferenciales?
-Despejar la derivada significa aislarla en uno de los lados de la ecuación, dejando todas las funciones de las otras variables del otro lado. Esto facilita la integración posterior para resolver la ecuación.
¿Cuáles son los componentes esenciales que se deben identificar en una ecuación diferencial separable?
-En una ecuación diferencial separable, es importante identificar los términos que contienen las funciones de las variables independientes y dependientes. Estos deben poder separarse en dos grupos distintos para permitir la integración por separado.
¿Qué ocurre si las letras en la ecuación no están multiplicadas entre sí?
-Si las letras (variables) en la ecuación no están multiplicadas entre sí, sino que están sumadas o combinadas de alguna otra manera, no es posible separarlas. Esto implica que la ecuación no es separable y requiere un enfoque diferente para resolverla.
En el video, ¿qué sucede cuando una ecuación tiene una multiplicación entre funciones con diferentes variables?
-Cuando una ecuación tiene una multiplicación entre funciones con diferentes variables, como en el caso de una función de x multiplicada por una función de y, la ecuación se puede separar y resolver, ya que las variables están involucradas de manera que se pueden aislar en ambos lados de la ecuación.
¿Por qué es importante saber integrar para resolver ecuaciones diferenciales?
-Es importante saber integrar porque la solución de muchas ecuaciones diferenciales implica realizar integrales para separar las variables y obtener una expresión de la función que satisface la ecuación original. Sin una comprensión sólida de la integración, no sería posible resolver estas ecuaciones.
En el ejercicio propuesto al final del video, ¿qué se debía identificar en las ecuaciones diferenciales?
-En el ejercicio propuesto, se debía identificar cuáles de las cuatro ecuaciones diferenciales eran de variables separables y cuáles no. Esto implicaba analizar la estructura de cada ecuación para determinar si se podía reorganizar de forma que las variables estuvieran separadas y pudieran integrarse por separado.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Variables Separables, video 1

0. ¿Qué es una Ecuación Diferencial? Tipos de ecuaciones diferenciales, solución de ED

ECUACIONES DIFERENCIALES EXACTAS. Curso completo de ecuaciones diferenciales desde cero

Ecuaciones diferenciales simples
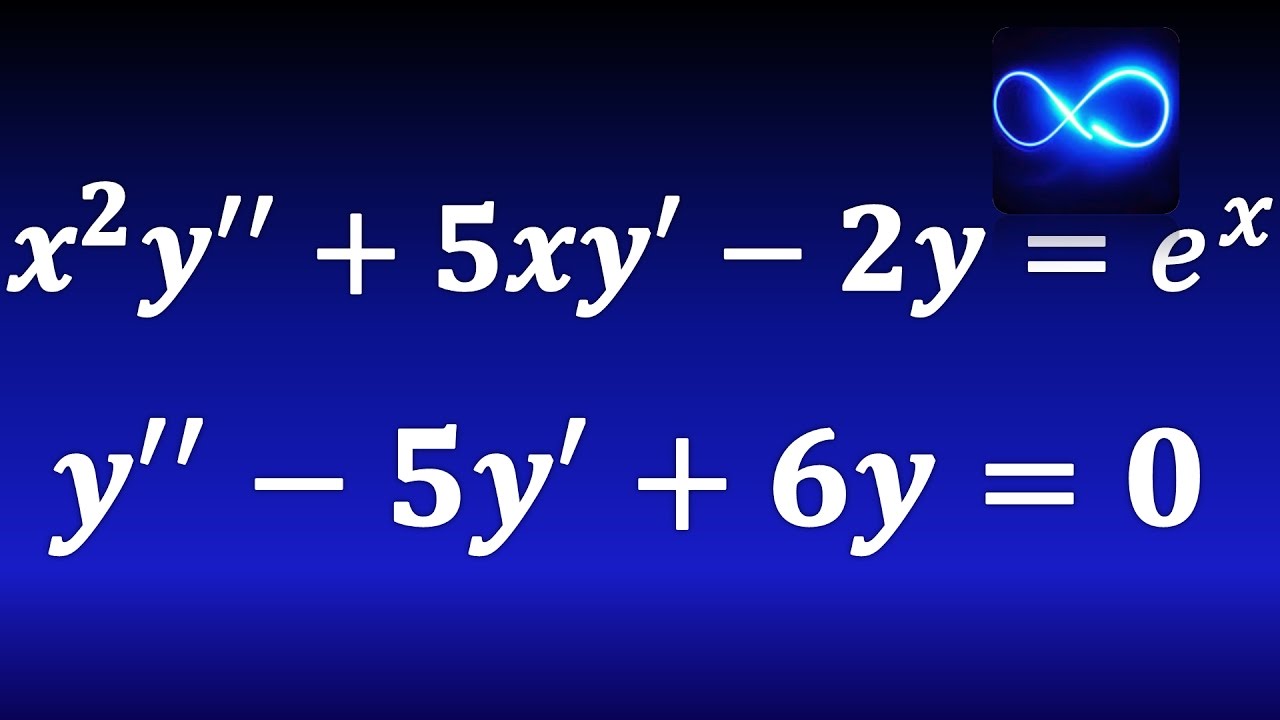
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
Ecuaciones diferenciales con Mathematica: Apliaciones de los sistemas de ecuaciones diferen | | UPV
5.0 / 5 (0 votes)
