Transformasi Geometri Bagian 2 - Refleksi (Pencerminan) Matematika Wajib Kelas 11
Summary
TLDRThis video script offers an educational exploration into the concept of geometric reflection, or 'refleksi' in Indonesian. The host, Handayani, guides viewers through the process of reflecting points and lines across various axes and lines, such as the x-axis, y-axis, and the line y=x. The explanation includes the transformation of coordinates, using both theoretical concepts and practical examples, such as reflecting a point across the origin or a specific line. The script also delves into solving reflection problems using matrices, providing formulas and step-by-step calculations for various reflection scenarios. The educational content is rounded off with several examples and exercises to solidify the viewers' understanding of geometric reflections.
Takeaways
- 📚 The video is an educational content about geometric transformations, specifically focusing on reflection or mirroring of points and lines in a Cartesian coordinate system.
- 🔍 The host introduces the concept of reflection by first explaining the basic idea of mirroring an object and its image with respect to a mirror, applying this concept to a flat mirror in a two-dimensional space.
- 📐 The video provides a step-by-step guide on how to find the coordinates of a reflected point over the x-axis and y-axis, using the formula for reflection: (x, y) becomes (-x, y) for the x-axis and (x, y) becomes (x, -y) for the y-axis.
- 📈 The script includes examples to illustrate the process of reflection, such as transforming the point (4, 2) to its mirror image over the x-axis resulting in the coordinates (-4, -2).
- 🤔 The video encourages viewers to actively participate in finding the formulas for reflection, fostering a learning environment where viewers are not just passive recipients of information.
- 📉 The concept of reflection over the line y = x is discussed, where the coordinates of a point are swapped, turning (x, y) into (y, x).
- 📍 The video explains how to reflect a point over the origin (0, 0), resulting in the coordinates becoming their negatives, e.g., (x, y) becomes (-x, -y).
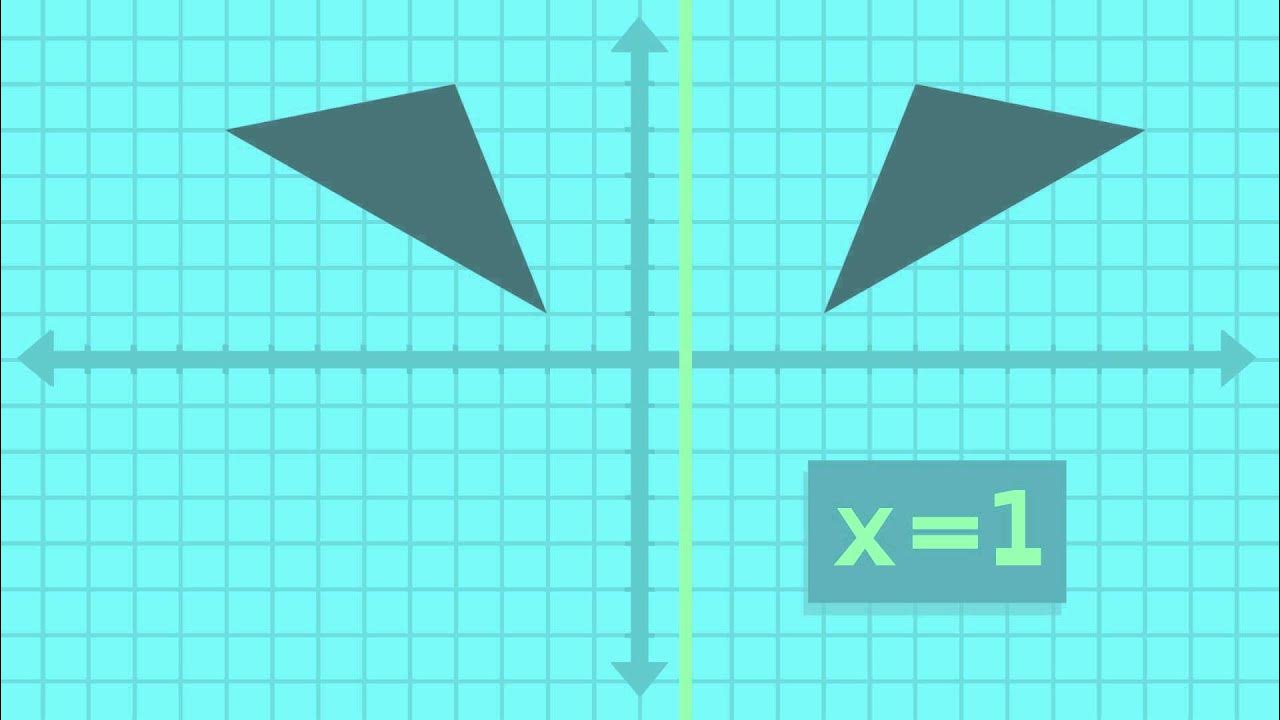
- 🔢 The script covers reflection over a vertical line x = h, where the y-coordinate changes its sign while the x-coordinate remains the same, e.g., (x, y) becomes (x, -y) when reflected over the line x = 2.
- 📘 The video also addresses reflection over a horizontal line y = k, with the x-coordinate changing its sign and the y-coordinate remaining constant, such as reflecting over y = 3 turning (4, 2) into (-4, 2).
- 📝 The host discusses the reflection of lines and curves, providing the method to determine the equation of the reflected line, using matrix transformations for lines like 3x + 2y - 1 = 0 over the line y = x.
- 🔄 The video concludes with the application of reflection using matrices, demonstrating how to calculate the reflected coordinates of points and the equations of reflected lines with examples.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the second type of geometric transformation, specifically reflection or mirroring of points, lines, and curves in a Cartesian coordinate system.
What is the formula for reflecting a point over the x-axis?
-The formula for reflecting a point (x, y) over the x-axis is (x, -y), where the x-coordinate remains the same and the y-coordinate changes its sign.
How does the reflection of a point over the y-axis differ from reflection over the x-axis?
-The reflection of a point over the y-axis results in changing the sign of the x-coordinate while keeping the y-coordinate the same, resulting in (-x, y).
What happens to the coordinates of a point when it is reflected over the line y = x?
-When a point is reflected over the line y = x, the coordinates of the point are swapped, resulting in the image point having the y-coordinate of the original point as its x-coordinate and vice versa.
Can you provide an example of a point reflected over the origin?
-An example of a point reflected over the origin (0, 0) would be a point (4, 2). Its reflection would be (-4, -2), with both coordinates changing their signs.
What is the reflection of a point over a horizontal line x = h?
-The reflection of a point (x, y) over a horizontal line x = h results in the x-coordinate changing to 2h - x, while the y-coordinate remains the same.
How do you reflect a point over a vertical line y = k?
-To reflect a point (x, y) over a vertical line y = k, the y-coordinate changes to 2k - y, while the x-coordinate remains unchanged.
What is the reflection of a line over the x-axis in terms of its equation?
-The reflection of a line over the x-axis changes the sign of the y-coefficients in its equation, resulting in a new line with the same x-coefficients and negated y-coefficients.
How can you reflect a line over the y-axis using its equation?
-To reflect a line over the y-axis, you negate the x-coefficients in its equation, resulting in a new line with the same y-coefficients and negated x-coefficients.
What is the reflection of a line over the line y = x in terms of its equation?
-The reflection of a line over the line y = x swaps the x and y coefficients in its equation, resulting in a new line where the roles of x and y are interchanged.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)