Statistics-Left Skewed And Right Skewed Distribution And Relation With Mean, Median And Mode

Summary

In this informative video, Krishnak discusses common examples of right and left skewed distributions, such as wealth distribution and human lifespan, and explains their characteristics. He also clarifies the relationship between mean, median, and mode in these distributions, noting that in right skew, mean > median > mode, while in symmetrical distributions like normal distribution, mean ≈ median ≈ mode, and in left skew, mode > median > mean. Krishnak emphasizes the importance of practical knowledge for better understanding and explanation of these concepts.

Takeaways

• 📚 The video discusses a statistical question related to skewness in data distributions that was asked in an interview.
• 📈 The script explains the concept of right skew distribution, where the right tail of the data distribution is elongated, compared to the left.
• 💰 Wealth distribution is given as a classic example of a right skew distribution, highlighting the few extremely wealthy individuals compared to the majority with less wealth.
• ✍️ The length of comments on the speaker's YouTube channel is used as another example of a right skew distribution.
• 📊 The script contrasts right skew distribution with symmetrical (normal) distribution, which includes examples like age, weight, and height distributions.
• 🌟 Machine learning algorithms often prefer data that follows a normal distribution, as it simplifies the modeling process.
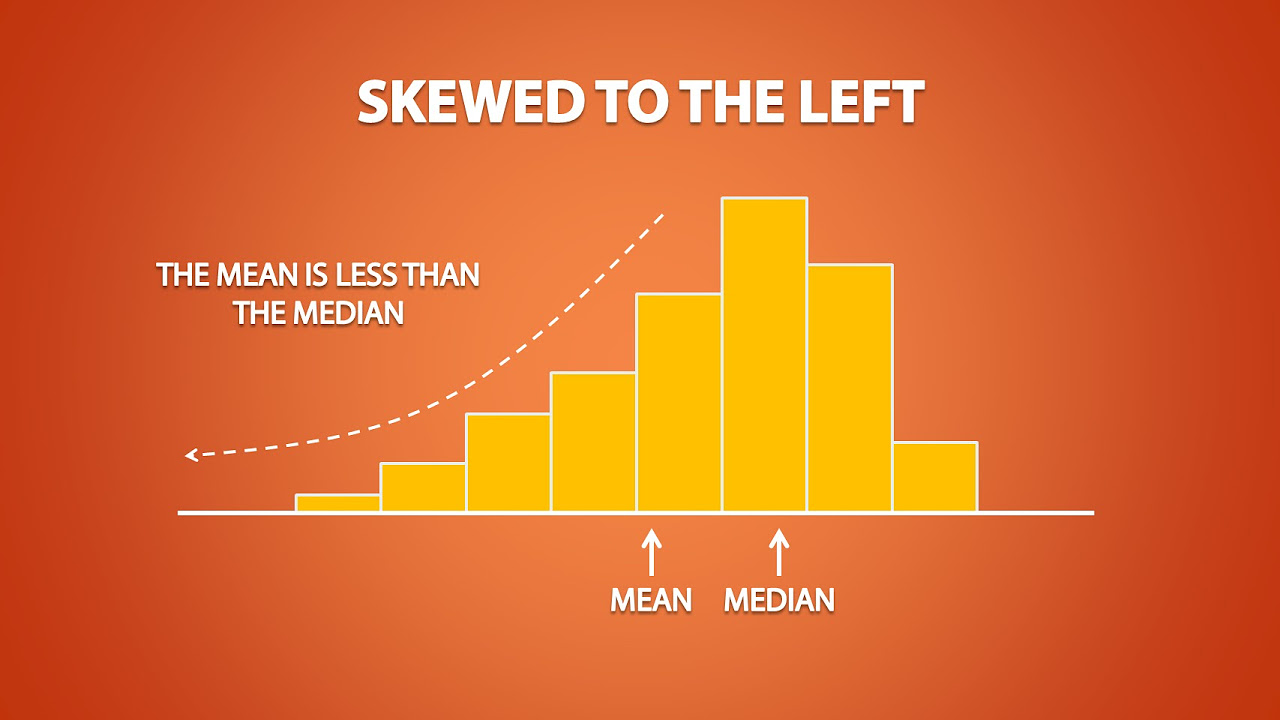
• 🔄 The left skew (or negative skew) distribution is also explained, with the lifespan of humans given as an example, where few live much longer than the average lifespan.
• 🔢 In a right skewed distribution, the mean is greater than the median, which in turn is greater than the mode.
• ⚖️ For symmetrical distributions, the mean, median, and mode are approximately equal, reflecting the balance of the data.
• 📉 In left skewed distributions, the mode is the highest, followed by the median, and then the mean, indicating the concentration of data towards the lower end.
• 🤓 The importance of understanding and being able to explain theoretical concepts with practical examples is emphasized for effective communication in interviews.

Q & A

What is the main topic discussed in the video?

The main topic discussed in the video is the concept of right skew distribution and left skew distribution, along with examples and the relationship between mean, median, and mode in these distributions.

What is a right skew distribution?

A right skew distribution, also known as a positively skewed distribution, is a type of distribution where the tail on the right side is longer or fatter than the left side, indicating that the data has a longer tail to the right.

Can you provide an example of a right skew distribution mentioned in the video?

One example of a right skew distribution mentioned in the video is wealth distribution, where a few extremely wealthy individuals like Elon Musk and Jeff Bezos represent the long tail on the right side of the distribution.

What is a left skew distribution?

A left skew distribution, also known as a negatively skewed distribution, is a type of distribution where the tail on the left side is longer or fatter than the right side, indicating that the data has a longer tail to the left.

Can you provide an example of a left skew distribution mentioned in the video?

The lifespan of human beings is given as an example of a left skew distribution, where there are fewer people living to very old ages compared to the average lifespan, creating a longer tail on the left side.

What is the relationship between the mean, median, and mode in a right skew distribution?

In a right skew distribution, the mean is greater than the median, and the median is greater than the mode. This is because the long tail on the right side pulls the mean to a higher value than the median.

What is the relationship between the mean, median, and mode in a left skew distribution?

In a left skew distribution, the mode is the highest, followed by the median, and then the mean. This is because the long tail on the left side pulls the mean to a lower value than the mode.

What is a symmetrical distribution and what is an example mentioned in the video?

A symmetrical distribution is one where the right and left sides of the distribution are mirror images of each other. An example mentioned in the video is the normal distribution, which is often seen in features like age, weight, and height in datasets.

What is the relationship between the mean, median, and mode in a symmetrical distribution?

In a symmetrical distribution, the mean, median, and mode are approximately equal, as the distribution is balanced with no skew to either side.

Why is it important to understand the relationship between mean, median, and mode in different types of distributions?

Understanding the relationship between mean, median, and mode in different distributions is important because it helps in interpreting the data correctly. It can indicate the presence of outliers, the central tendency, and the skewness of the data, which are crucial for data analysis and decision-making.

How can one remember the relationship between mean, median, and mode in different distributions?

One can remember the relationship by visualizing the distribution diagrams and associating the positions of mean, median, and mode with the direction of the skew. For right skew, mean > median > mode; for symmetrical, mean ≈ median ≈ mode; for left skew, mode > median > mean.

Outlines

00:00

📊 Introduction to Skewness in Data Distribution

Krishnak introduces a statistical question from a recent interview, focusing on right and left skew distributions. He explains the concept of skewness by describing the shape of a histogram or kernel density estimator and provides examples of right-skewed data, such as wealth distribution featuring billionaires like Elon Musk and Bill Gates. He also mentions the length of comments on his YouTube channel as another example. The explanation is aimed at helping viewers understand the basic concept of skewness and its practical applications.

05:02

📚 Understanding Mean, Median, and Mode in Skewed Distributions

The second paragraph delves into the relationship between mean, median, and mode in different types of distributions. Krishnak clarifies that in a right-skewed distribution, the mean is greater than the median, which in turn is greater than the mode. For a symmetrical distribution, like the normal distribution, the mean, median, and mode are approximately equal. In contrast, for a left-skewed or negative skew distribution, the mode is the highest, followed by the median and then the mean. Krishnak emphasizes the importance of knowing examples to explain these concepts effectively and encourages viewers to apply theoretical knowledge to practical scenarios.

Keywords

💡Right Skew Distribution

Right skew distribution, also known as positive skew, is a type of data distribution where the tail on the right side is longer or fatter than the left side. This indicates that the majority of the data points are concentrated on the lower end, with fewer data points spread out towards the higher end. In the video, wealth distribution is given as a classic example where a few extremely wealthy individuals like Elon Musk and Jeff Bezos represent the long tail on the right, while the majority of people have less wealth.

💡Left Skew Distribution

Left skew distribution, or negative skew, is the opposite of right skew, where the tail on the left side of the distribution is longer. This means that the data points are more spread out towards the lower values, with fewer points at the higher end. The lifespan of human beings is used as an example in the video, where many people die at a younger age, but a smaller number live well beyond the average lifespan, creating a long tail on the left.

💡Symmetric Distribution

A symmetric distribution is one where the data is evenly spread out around a central point, with both ends mirroring each other. The normal distribution, or Gaussian distribution, is a prime example of this, where the mean, median, and mode are all equal. The video mentions that many features in machine learning datasets, such as those in the iris dataset, follow this distribution, which is preferred by most machine learning algorithms.

💡Mean

The mean, often referred to as the average, is a measure of central tendency that is calculated by summing all the values in a dataset and then dividing by the number of values. In the context of the video, the mean is discussed in relation to skewed distributions, where in a right skew, the mean is greater than the median due to the influence of extreme values on the right.

💡Median

The median is the middle value of a dataset when the values are arranged in ascending order. It is less affected by extreme values compared to the mean. In the video, the median is explained as being less than the mean in a right-skewed distribution and approximately equal to the mean in a symmetric distribution.

💡Mode

The mode is the value that appears most frequently in a dataset. It is a measure of central tendency that can be used for both numerical and categorical data. In the video, the mode is described as being the smallest of the three measures of central tendency in a left-skewed distribution and the smallest in a right-skewed distribution.

💡Histogram

A histogram is a graphical representation of the distribution of data, where data is grouped into bins or intervals, and the frequency of data points within each bin is represented by the height of the bars. In the video, histograms are mentioned as a way to visualize the skewness of a distribution, with right-skewed histograms having a long tail on the right side.

💡Kernel Density Estimator

A kernel density estimator (KDE) is a way to visualize the distribution of data by smoothing the histogram into a continuous curve. It is used to estimate the probability density function of a continuous random variable. The video script mentions KDE as a method to identify the skewness of data distributions.

💡Interview Question

The term 'interview question' in the video refers to the practice of preparing for job interviews by understanding and practicing responses to common and challenging questions. The video discusses a specific interview question related to statistical distributions, highlighting the importance of knowing both theoretical concepts and practical examples.

💡Comment Length

Comment length is used as an example in the video to illustrate a right-skewed distribution in a non-traditional context. It refers to the varying lengths of comments people leave on videos, with some individuals writing very long comments, while most write shorter ones, creating a distribution that is skewed to the right.

💡Iris Dataset

The iris dataset is a classic in the field of machine learning and statistics, often used for teaching and testing clustering algorithms. In the video, it is mentioned as an example of a dataset where features like petal length and width follow a symmetric distribution, which is ideal for many machine learning models.

Highlights

Introduction to the YouTube channel and the purpose of sharing interview questions.

The importance of uploading interview questions to an interview playlist for future reference.

A recent interview question about classical examples of right and left skew distributions.

Explanation of what constitutes a right skew distribution in data.

Wealth distribution as a classical example of a right skew distribution.

Length of comments on videos as an example of right skew distribution.

Introduction to symmetrical distribution, also known as normal distribution.

Examples of normal distribution in features of machine learning algorithms.

Iris dataset features following a normal distribution.

Definition and explanation of left skew or negative skew distribution.

Lifespan of humans as an example of a left skew distribution.

The relationship between mean, median, and mode in right skew distribution.

Mean being greater than median, which in turn is greater than mode in right skew distribution.

Mean, median, and mode being approximately equal in symmetrical distribution.

In left skew distribution, mode is the highest, followed by median and then mean.

The significance of understanding and remembering examples for explaining theoretical concepts.

Encouragement for viewers to subscribe to the channel for more interview question insights.

Transcripts

hello all my name is krishnak and

welcome to my youtube channel so guys

morning ad actually asked you a

statistical question which was recently

asked

in an interview to one of my subscriber

as you all know guys

most of the interview questions

whichever i get to know i am definitely

uploading that in my interview playlist

and whenever i find out any new

questions i'll probably make a video

with respect to that

so let me just tell you what was the

question basically asked and for that

in the morning also i had actually

created a video many of you

actually gave the right answer and yes

many of you were also actually confused

okay with respect to the question that i

had asked so the question was that

just tell us some of the classical

examples of

the right skew distribution and the left

skid distribution

and the second question was that what is

the relationship between the mean

median mode of right skill distribution

and the left skill distribution now

first of all we'll try to understand

what exactly is right skew distribution

and left skill distribution

now guys whatever data you take and

probably if you're trying to

plot it in the form of histogram in the

form of

kernel density estimator and whenever

you see

this kind of right hand side elongated

line right like this like this kind of

distribution this is basically called as

right skewed data okay

that basically means your right side

right hand side of this particular curve

is little bit elongated when compared to

the left hand side right

now some of the classical examples over

here so i'm just going to take some of

the example

the first example that i would like to

take is wealth

distribution this is a very classical

example

which recruiters also like to hear just

imagine some of the top most richest

people like elon musk

jeff from amazon mark zuckerberg bill

gates they usually fall in this

particular region

even ambani and they are very less

number of people

you know who follows in this specific

reason whereas

in this particular region you will be

finding people with the same amount of

wealth

right this is one classical example the

second classical example that i would

like to take

is probably you can you know that like

you have seen my channel you have seen

most of my videos guys you'll be seeing

that some of the people like to

write a longer comments right probably

after seeing a video

so length of the comments

length of comments probably in my video

this is also a classical example

right so here you'll be seeing that some

of the people will be writing

longer comments they are also some of

the people who will be writing smaller

comments and some of the people

will most of the people will be writing

medium size comment probably one liner

right so this is two classical examples

that i want to give

yes in the morning video many people

gave some amazing examples itself

right and you should also check out that

again the link will be given in

description

now coming to the second uh distribution

second distribution which is called a

symmetrical distribution this is nothing

but our

normal distribution this is the example

normal distribution i think we have

worked out normal distribution with

respect to our machine learning problem

statement

i'll get some of the algorithms once all

of the features falling in this kind of

most of the features falling in this

kind of distribution itself

some of the classical example is that

age distribution

probably weight distribution uh

probably height distribution they all

follow this kind of normal distribution

and even if you have worked with iris

data set you saw that in the iris data

set you had features like petal length

petalwidth sepal length and

weight right that was also following

this kind of normal distribution

and remember guys most of the machine

learning algorithm likes the data

to have this kind of normal distribution

property or

and why it is called a symmetrical

distribution because the right hand

curve

will almost be equal to the left hand

curve okay

so these are like mirror phase fine

coming to the third kind of distribution

which is also called as

left cube distribution it is also called

as negative skew distribution

here the left hand side will be little

bit elongated

and then the right hand side right so

here the perfect example i'll say

lifespan of human being

lifespan of human being

because there are many people if i talk

about the average lifespan

it is somewhere around 50 to 70 so 50 to

70 will basically be falling in this

particular region

there will be people who will be dying

quite early in the age

but they will be also very less number

of people who will be living more than

70 years probably near 100 and all

again a perfect example to make you

understand yes

if you have some more examples

definitely many people had also written

in the morning

and i i like most of the examples itself

right

now coming to the second question what

is the exact relationship with respect

to mean median and mode

it is very very much simple just by

seeing this particular diagram i think

you will be able to know it guys

mean in the right skewed distribution

over here will be greater than median

and median will be greater than mode

right so mean will be greater than

median and median will be greater than

mode so this is the exact relationship

that you will be able to find

just by seeing this particular diagram

will be able to understand in the case

of symmetrical distribution

mean will be approximately equal to

median it will be approximately equal to

mode so this is the second relationship

that you find out with respect to normal

distribution

the third one basically what you see

over here if i take this particular

example over here your mode is highest

then your median then your

mean right so this is the exact

relationship let me just write it down

if you are getting confused

first the highest will be mode

then your median you have because median

will be obviously smaller than mode

then you have mean so this is the

relationship that you find out with

respect to the

negative skewed data so this

is what the interviewer may be expecting

probably remember whenever this kind of

questions are asked always make sure

that you know some of the examples

because if you tend to forget this

particular topics also

just with the help of those examples

will be able to explain it in a proper

way

trust me guys practical knowledge

definitely understanding of that

theoretical is very very much important

if you are able to relate this

theoretical thing with some practical

stuff

you will be able to understand you will

be able to relate once you able to

relate it

you will be able to understand you will

be able to explain it okay

so this is what i really wanted to cover

just let me know whether

you like this kind of thing or not

because every day i'll at least come up

with one interview questions probably

and then i'll try to explain you

completely from end to end so i hope you

like this particular video please do

subscribe the channel if you're not

already subscribed i'll see you in the

next video have a great day ahead

thank you and all bye