Perceptron Learning Algorithm

Summary

This lecture delves into supervised learning, focusing on binary classification and the distinction between generative and discriminative models. It highlights the Naive Bayes algorithm as a generative model and contrasts it with discriminative models like K-Nearest Neighbors and decision trees. The instructor introduces the Perceptron algorithm, developed by Rosenblatt in the 1950s, emphasizing its application in linearly separable datasets. The Perceptron's iterative process updates weights to minimize the zero-one loss, aiming for a model that perfectly classifies all data points, contingent on the linear separability assumption.

Takeaways

• 📚 The course focuses on supervised learning, specifically binary classification algorithms, and distinguishes between generative and discriminative models.
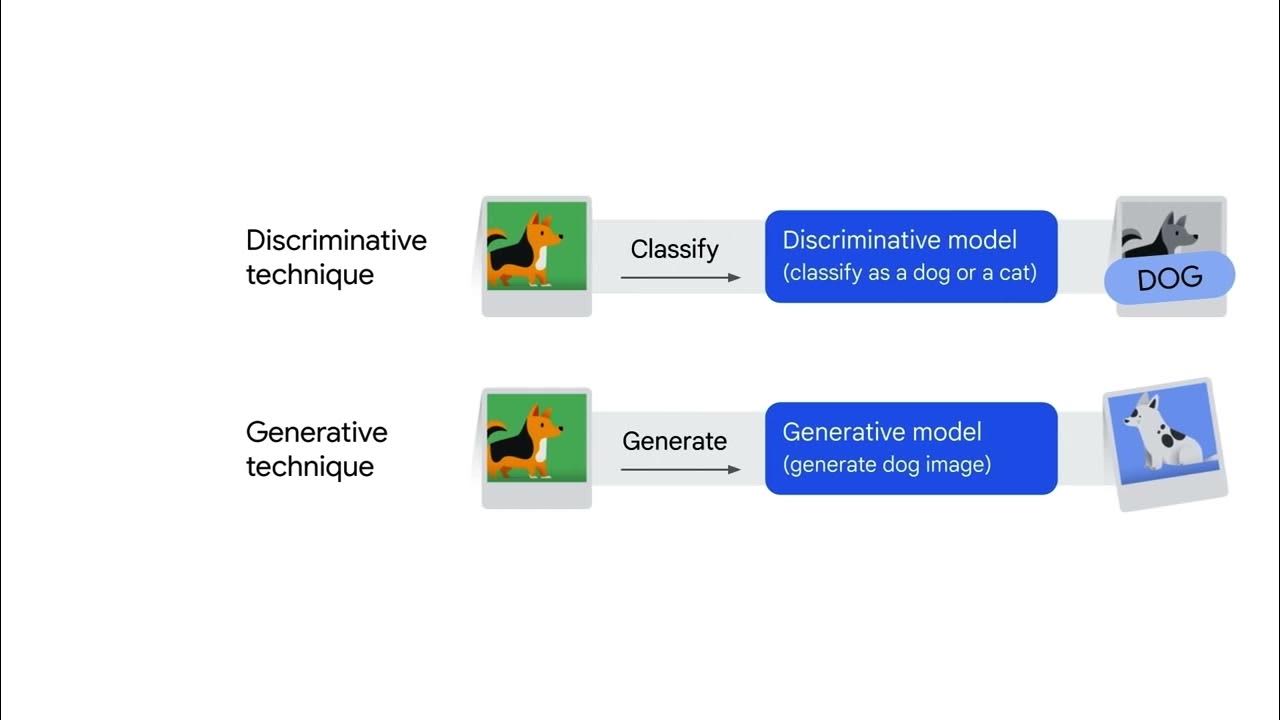
• 🔍 Generative models, like Naive Bayes, assume class-conditional independence and are used to model the joint probability of features and labels.
• 📈 Discriminative models, such as K-Nearest Neighbors and Decision Trees, predict outcomes based on data points without modeling the data's generation process.
• 🤖 The Perceptron algorithm, introduced by Frank Rosenblatt in the 1950s, is a linear classifier that updates weights iteratively to classify data points correctly.
• 🧠 The Perceptron is inspired by biological neurons and synapses, aiming to mimic the decision-making process of the human brain.
• 🔄 The algorithm begins with an initial weight vector of zero and iteratively updates the weights by adding misclassified points multiplied by their labels.
• ✅ The Perceptron converges when it finds a weight vector that correctly classifies all data points in the training set, achieving zero training error.
• 🚫 The Perceptron algorithm assumes linear separability, meaning there exists a hyperplane that can perfectly separate different classes in the feature space.
• 📉 The algorithm may fail to converge if the data is not linearly separable, highlighting a limitation of this model.
• 🔢 The update rule of the Perceptron is crucial for its convergence, where the weight vector is adjusted based on the error made on each misclassified point.
• 🔮 The script discusses the theoretical aspects of the Perceptron, including its assumptions, update rule, and conditions for convergence, providing foundational knowledge for understanding machine learning algorithms.

Q & A

What are the two broad ways of modeling a binary classification problem discussed in the script?

The two broad ways of modeling a binary classification problem are the generative model and the discriminative model.

What is the Naive Bayes assumption in the context of the generative model?

The Naive Bayes assumption is that it assumes class-conditional independence, which means it assumes that the presence of a particular feature in a class is unrelated to the presence of any other feature.

What is the difference between Gaussian Naive Bayes and Gaussian Discriminant Analysis mentioned in the script?

Gaussian Naive Bayes and Gaussian Discriminant Analysis are actually the same algorithm, which is used when features are assumed to be normally distributed. The difference in names is just a matter of terminology.

Why are K-Nearest Neighbors and decision trees considered discriminative models?

K-Nearest Neighbors and decision trees are considered discriminative models because they do not model how the data is generated. Instead, they focus on making predictions based on the data points given.

What is the fundamental assumption made by the perceptron algorithm?

The fundamental assumption made by the perceptron algorithm is that the data is linearly separable, meaning there exists a hyperplane that can perfectly separate the different classes in the feature space.

How does the perceptron algorithm handle the probability of y given X?

The perceptron algorithm simplifies the problem by assuming a deterministic relationship where the probability of y given X is either 1 or 0, based on whether the weighted sum of the features (W transpose X) is greater than or equal to zero.

What is the perceptron algorithm's update rule, and when is it applied?

The update rule of the perceptron algorithm is to add the instance (xi) multiplied by its label (yi) to the current weight vector (w) when the current weight vector misclassifies the instance (i.e., sign(w^T * xi) does not equal yi).

What does the perceptron algorithm aim to find, and how does it start?

The perceptron algorithm aims to find a weight vector (w) that correctly classifies all the data points in the dataset. It starts with an initial weight vector of zero.

How does the script describe the convergence of the perceptron algorithm?

The script describes the convergence of the perceptron algorithm as the point when it finds a weight vector that correctly classifies all the data points, at which no more updates are needed.

What is the significance of the perceptron algorithm in the history of machine learning?

The perceptron algorithm is significant as it was one of the earliest algorithms developed for machine learning, inspired by the biological structure of neurons, and it laid the groundwork for understanding classical machine learning.