SHS General Physics 1 | Lesson 3: VECTOR ADDITION

Summary

In this lesson, students will learn about vectors, including differentiating vectors and scalar quantities, performing vector addition, and rewriting vectors in component form. The lesson begins with a review of trigonometric functions and the law of cosines. It covers vector representation, addition of parallel and non-parallel vectors, and methods like the tip-to-tail and parallelogram methods for finding resultant vectors. The lesson also includes numerical analysis for calculating resultant forces and introduces unit vectors and their calculations. Practical examples and problems are provided for better understanding. Students are assigned activities to reinforce the concepts learned.

Takeaways

• 📚 The lesson covers vectors, including differentiation between vectors and scalars, vector addition, and writing vectors in component form.
• 📐 Quick review of SOHCAHTOA: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent.
• 🔢 Example problem solving: For a 30-degree triangle with given sides, calculating sine, cosine, and tangent.
• 🔺 Law of cosines: Useful for finding a third side of a triangle when two sides and the angle between them are known, or finding angles when all three sides are known.
• 🛠️ Scalars are quantities described by magnitude only, such as speed, volume, mass, and time.
• ➡️ Vectors have both magnitude and direction, important in motion studies; examples include force, velocity, acceleration, and momentum.
• 📏 Representation of vectors: Typically a letter with an arrow above or in boldface, and the magnitude is shown without an arrow or with vertical bars.
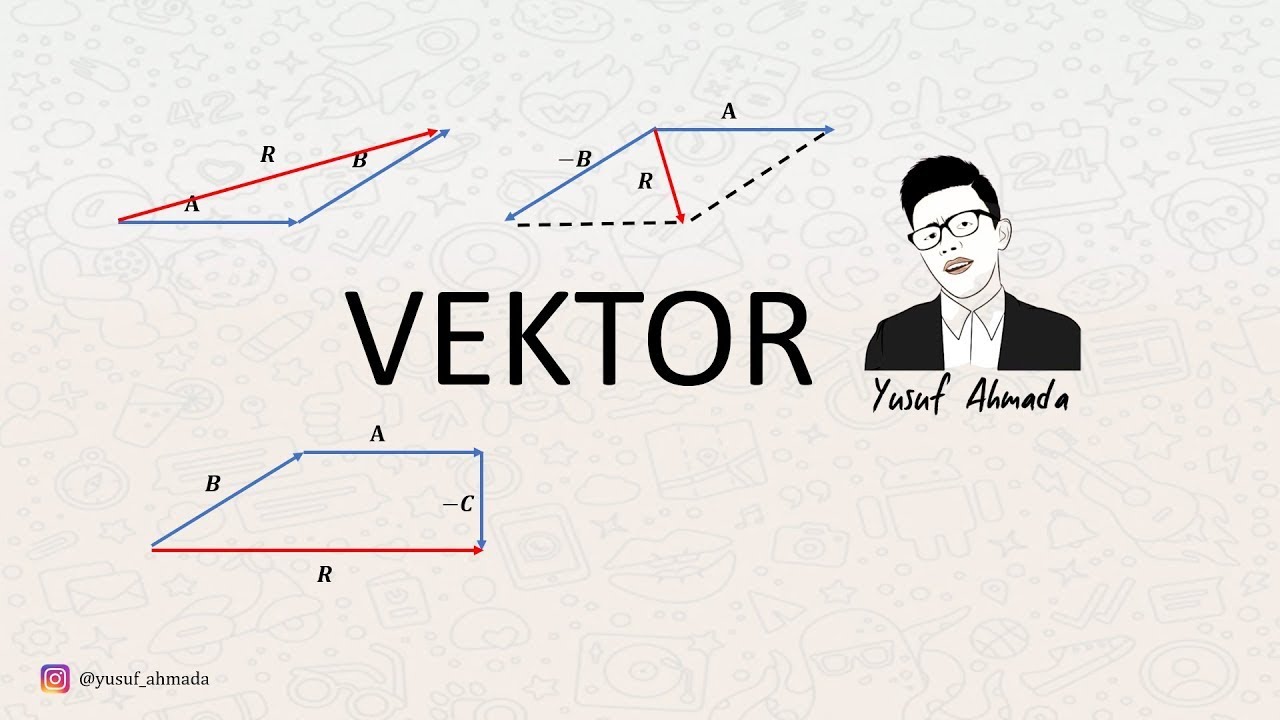
• ➕ Vector addition: Adding corresponding components of vectors to find the resultant vector.
• 🔄 Adding parallel and non-parallel vectors: Use direction consideration for parallel vectors and tip-to-tail or parallelogram methods for non-parallel vectors.
• 📊 Numerical analysis: Law of cosines and Pythagorean theorem can be used for calculating resultant forces in non-graphical methods.

Q & A

What are the objectives of today's lesson on vectors?

The objectives are to differentiate vectors and scalar quantities, perform addition of vectors, and rewrite a vector in component form.

What is SOHCAHTOA and how is it used?

SOHCAHTOA is a mnemonic to remember the definitions of sine, cosine, and tangent: Sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent.

How do you solve for sine, cosine, and tangent in a 30-degree triangle with given side lengths?

For sine, divide the opposite side (1) by the hypotenuse (2) to get 0.5. For cosine, divide the adjacent side (√3) by the hypotenuse (2) to get 0.866. For tangent, divide the opposite side (1) by the adjacent side (√3) to get 0.577.

What is the law of cosines and when is it useful?

The law of cosines is useful for finding the third side of a triangle when two sides and the angle between them are known, or for finding the angles when all three sides are known. The formula is c² = a² + b² - 2ab * cos(C).

What is the difference between a scalar and a vector quantity?

A scalar quantity is described by a magnitude only, while a vector quantity has both a magnitude and a direction.

How are vectors typically represented?

Vectors are usually represented by a letter with an arrow above it or in boldface. The magnitude of a vector can be represented by a lightface letter without an arrow or the vector symbol with vertical bars on both sides.

How do you add two vectors in component form?

To add two vectors in component form, you add their corresponding components. For example, vector A (2, 4) + vector B (-1, 6) results in vector C (1, 10).

How do you add parallel vectors?

For parallel vectors in the same direction, you add their magnitudes. For vectors in opposite directions, you subtract their magnitudes.

What methods can be used to add non-parallel vectors?

The tip-to-tail method and the parallelogram method can be used to add non-parallel vectors.

How can you calculate the resultant force using the law of cosines?

Using the law of cosines, you can calculate the resultant force by applying the formula: R² = a² + b² - 2ab * cos(C). Then, solve for R.

What is a unit vector and how is it calculated?

A unit vector has a magnitude of one and is used to indicate direction. It is calculated by dividing each component of the vector by the vector's magnitude.

How can you find the direction of a vector using trigonometry?

The direction of a vector can be found using the arctangent function: θ = arctan(b/a), where b and a are the components of the vector.

What is the process for finding the net force when multiple forces act at different angles?

To find the net force, break each force into its x and y components, sum the components separately, then use the Pythagorean theorem to find the resultant magnitude and arctangent to find the direction.

What activities were assigned at the end of the lesson?

The activities assigned are: Activity 1 on page 13, Activity 2 on page 14, Activity 3 on page 15, and Activity 4 on page 16.

Outlines

00:00

🎓 Introduction to Vectors and Scalars

This lesson covers vectors and scalar quantities. By the end, students will be able to differentiate between vectors and scalars, perform vector addition, and rewrite vectors in component form. A review of SOHCAHTOA helps refresh knowledge on sine, cosine, and tangent functions. The lesson also recalls the law of cosines, useful for finding triangle sides or angles. Scalars, described by magnitude alone, include quantities like speed and mass. Vectors, which have both magnitude and direction, include force and velocity.

05:03

➕ Vector Representation and Addition

This section explains how vectors are represented, with arrows or bold letters for vectors and lightface letters or bars for magnitudes. It discusses vector components, which are ordered pairs describing changes in x and y values. Vectors are equal if they have the same magnitude and direction. Vector addition is performed by adding corresponding components. Examples include adding vectors and handling parallel vectors by considering their directions, resulting in net forces based on their magnitudes and directions.

10:05

📐 Methods for Adding Non-Parallel Vectors

This part covers methods for adding non-parallel vectors using the parallelogram method and tip-to-tail method. An example is given with forces of 75N and 50N at a 60-degree angle. The parallelogram method involves redrawing diagrams to scale and finding the resultant force as the diagonal. The tip-to-tail method involves drawing arrows representing forces and finding the resultant by connecting the starting point of the first force to the endpoint of the second. Numerical analysis is introduced to calculate resultants using the law of cosines.

📏 Numerical Analysis of Vectors

This section illustrates solving vector problems numerically. For example, calculating the resultant force using the law of cosines when given two sides and an angle. Another example involves a weight of 8N pulled sideways by a 5N force, using the Pythagorean theorem to find the resultant. Unit vectors, which have a magnitude of one, are explained. Calculations for unit vectors in two and three dimensions are demonstrated, and vector addition/subtraction using components is shown. Magnitude and direction of vectors can be calculated using specific formulas.

⚖️ Advanced Vector Problems and Activities

This final section presents complex vector problems, such as calculating the net force from multiple forces at different angles. It involves breaking forces into x and y components and using trigonometric functions to determine these components. The resultant is found by summing the components and applying the Pythagorean theorem. The direction is found using the arctan function. The section concludes with assigned activities from the textbook, reinforcing the lesson's concepts through practice problems.

Keywords

💡Vectors

Vectors are quantities that have both magnitude and direction. In the video, vectors are fundamental to understanding various physical phenomena such as force, velocity, and acceleration. For example, the script discusses vector addition and representation, showing how vectors are combined to find a resultant force.

💡Scalars

Scalars are quantities described by only a magnitude, without direction. Examples given in the script include speed, volume, mass, and time. Scalars are contrasted with vectors to highlight the importance of direction in certain physical quantities.

💡Addition of Vectors

This process involves combining vectors to find a resultant vector. The script explains methods like the parallelogram and tip-to-tail methods to visually and mathematically add vectors. For instance, adding vectors with components (2,4) and (-1,6) results in (1,10).

💡Component Form

The component form of a vector describes its projection along the x and y axes. The script explains how vectors can be represented as ordered pairs (x, y), making it easier to perform operations like addition and subtraction. For example, vector A (2, 4) has components 2 in the x direction and 4 in the y direction.

💡Resultant

The resultant is the vector sum of two or more vectors. It represents the combined effect of the vectors. In the script, the resultant is found by adding the components of the vectors. For example, the resultant of vectors A and B is shown as the arrow between them.

💡Parallelogram Method

A graphical technique to add vectors, where vectors are represented as adjacent sides of a parallelogram. The diagonal of the parallelogram represents the resultant vector. The script details this method using a 75 N and 50 N force example.

💡Tip-to-Tail Method

Another graphical method for vector addition, where the tail of one vector is placed at the tip of the other. The resultant vector is drawn from the tail of the first to the tip of the second vector. The script demonstrates this with a 75 N and 50 N force.

💡Law of Cosines

A mathematical formula used to find unknown sides or angles in a triangle, particularly useful when vectors form a triangle. The script explains its application in determining the resultant vector in non-parallel vector addition.

💡Unit Vector

A vector with a magnitude of one, used to indicate direction. The script explains how unit vectors are calculated and used in vector analysis, such as representing vector A in terms of its unit vectors.

💡Pythagorean Theorem

A fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. The script uses this theorem to calculate the resultant of perpendicular vectors.

💡Magnitude

The size or length of a vector. The script explains how to calculate the magnitude of a vector using the Pythagorean theorem, which is crucial for finding the length of the resultant vector in various examples.

Highlights

Differentiate between vectors and scalar quantities.

Perform addition of vectors.

Rewrite a vector in component form.

Recall the basic trigonometric functions: sine, cosine, and tangent.

Example problem involving a 30-degree triangle with specific side lengths.

Explanation of the law of cosines for finding sides or angles of a triangle.

Definition and examples of scalar quantities like speed, volume, mass, and time.

Definition and examples of vector quantities like force, velocity, acceleration, and momentum.

Representation of vectors using letters with arrows or boldface letters.

Component form of a vector as an ordered pair describing changes in x and y values.

Methods for adding vectors: summing corresponding components and graphical methods like the parallelogram method.

Adding parallel vectors by considering direction: sum for the same direction, subtract for opposing directions.

Non-parallel vector addition using the tip-to-tail method and the parallelogram method.

Example problem using the parallelogram method to find the resultant of two non-parallel forces.

Introduction of unit vectors as vectors with a magnitude of one unit, often used to denote direction.

Algebraic addition and subtraction of vectors using their components.

Calculating the magnitude and direction of a vector using the Pythagorean theorem and trigonometric functions.

Example problem involving three forces acting on a point, requiring summation of x and y components.

Transcripts

[Music]

hello dear students

our lesson for today is all about

vectors

at the end of this lesson you will be

able to

1. differentiate vectors and scalar

quantities

two perform addition of vectors and

three

rewrite a vector in component form

before we start

let us have a short review about sokodoa

we all know that it is just an easy way

to remember how sine

cosine and tangent works for sine it is

always opposite over hypotenuse

for cosine it is adjacent over

hypotenuse

and for tangent it is opposite over

adjacent

to refresh your knowledge let us answer

this simple problem

a 30 degree triangle has a hypotenuse of

length 2

an opposite side of length 1 and an

adjacent side of square root of 3

as shown on the figure now try solving

for the functions

for sine we get 0.5 by dividing opposite

magnitude of 1 with the hypotenuse

magnitude of 2.

for cosine we get 0.866 by dividing the

adjacent magnitude of square root of 3

with the hypotenuse magnitude of 2.

lastly for tangent we get 0.577

by dividing the opposite magnitude of 1

with the adjacent magnitude of square

root of 3.

for this lesson it is also important

that we recall the law of cosines

the law of cosines is useful for finding

either

the third side of a triangle when we

know two sides and the angle between

them

or the angles of a triangle when we know

all three sides

let us now continue with our lesson

vectors and scalars

a scalar is a quantity that is fully

described by a magnitude only

it is described by just a single number

some examples of scalar quantities

include speed

volume mass and time on the other hand

a vector is a quantity that has both a

magnitude and a direction

vector quantities are important in the

study of motion

some examples of vector quantities

include force velocity

acceleration and momentum the following

are the parameters considered as vectors

lift displacement weight drag force

momentum acceleration and velocity

for scalar we have time distance mass

volume area density work temperature

speed energy and power representation of

vectors

a vector is usually represented by

either a letter with an arrow above the

letter or a bold face letter

the magnitude of a vector is represented

by either a light face letter without an

arrow on top

or the vector symbol with vertical bars

on both sides

component of a vector the component form

of a vector is the ordered pair that

describes the changes in the x and y

values

we can say that two vectors are equal if

they have the same magnitude and

direction

or when they are parallel if they have

the same or opposite direction

we can combine vectors by adding them

the sum of two vectors is called the

resultant

in this picture the resultant is the

arrow between the vectors and b

in order to add two vectors we add the

corresponding components

example add the two following vectors

vector a with ordered pair two and four

and vector b with ordered pair negative

one and six

we add the corresponding components as

shown

vector of plus vector b equals two plus

negative one

and four plus six the answer is one and

ten

adding parallel vectors to add parallel

vectors

we just need to consider the direction

we add vectors in the same direction

and subtract those who oppose each other

for the first example

the forces 1 newton and 1.5 newton are

both directed to the right

so the f net will be one plus 1.5 equals

to 2.5 newtons to the right

for the second example the forces 1

newton and 1.5 newton are both directed

to the left

while 1.5 newton is directed to the

right

the f net will be 1.5 plus 1 minus 1.5

we get 1 newton to the left

non-parallel forces to add non-parallel

forces we use two methods

tip to tail method parallelogram method

let us answer this example while

illustrating how to use the two methods

consider two forces that are not acting

along the same line on an object

find the resultant force f1 is 75

newtons

while f2 is 50 newtons the angle between

them is 60 degrees

using the parallelogram method step 1

redraw the given diagram using a

suitable scale to represent the forces

with arrows

note 1 centimeter represents 10 newtons

so 75 n equals 7.5 centimeters and 50 n

equals 5 centimeters

step 2 complete a parallelogram to scale

step 3 the resultant force is

represented by the diagonal of the

parallelogram

find the magnitude and direction of the

resultant force to scale

measuring the length of the yellow line

we get f net equals 10.6 times

10 equals 106n at an angle of 25 to the

power of 0 from 75n

tip to tail method step 1 draw an arrow

to represent one of the two forces using

a suitable scale

note 1 centimeter represents 10 newtons

so 50 n equals 5 centimeters

step 2 where the first arrow ends draw

another arrow to represent the second

force 75n so that the tip of the first

arrow joins the tail of the second arrow

step 3 the resultant force is found by

joining the starting point of first

force to the endpoint of second force

find the magnitude and direction of the

resultant force to scale

measuring the resultant represented by

the yellow line

f net equals 10.6 times 10 equals 106n

at an angle of 35 to the power of 0 from

50n

[Music]

you may have observed that the recent

methods are graphical and you may be

worried that it will consume time

however we can calculate the resultant

numerically so you have nothing to worry

for the numerical analysis first observe

the figure on the bottom

the connected lines formed a triangle

which means

we can use any method that we know can

solve a triangle

look closely we are given two sides and

an angle between the adjacent side and

the hypotenuse

[Music]

through the given we can conclude that

we can use the law of cosines

the formulas for the law of cosines are

shown in the picture

now using the cosine law we can compute

for the resultant

r r squared is equals to the square of

adjacent side

plus the opposite side minus the product

of twice the two sides and cause of the

angle opposite the hypotenuse

r that we are looking for typing this on

your calculators we get 108.97

next example a weight of eight newtons

hangs from the end of a row

it is pulled sideways by a horizontal

force f of five

n and is held stationary what is t

we can draw the figure using the

parallelogram method and the tip-to-tail

method

like what is shown in the picture below

to solve this using a numerical analysis

let us focus on figure enclosed in a red

shape

looking closely observe that the shape

formed by connecting the lines is a

right triangle

because of this we can use the

pythagorean theorem to solve for the

resultant

just square the sides and add them then

get the square root of their sum

we get t equals 9.4339

unit vector a unit vector is a vector

that has a magnitude of one unit

a unit vector is also known as a

direction vector

the symbol for the unit vector is

usually a lower case letter with a hat

such as shown in the picture the unit

vector of a vector can be calculated

using the given formula

unit vector is equals to the ratio of 1

and the magnitude of the given vector

where the magnitude of the vector can be

calculated by getting the square root of

the sum of the squares of the ordered

pair

unit vectors can be used in two

dimensions here we show that the vector

a is made up of two

x unit vectors and 1.3 y unit vectors

likewise we can use unit vectors in

three or more

dimensions

[Music]

we can add or subtract vectors

algebraically using the vector

components

using the given vectors let us try a

minus c

a c equals 4 sub x i plus 5 sub z k

minus 7 sub y j minus 8 sub z k

reordering the components with the same

variables we arrive at 4 sub x minus 7

sub j

plus 13 sub z k

[Music]

we can compute for the magnitude of the

vector and find its direction using the

formula shown

for the direction we use theta is equals

to arc tan of b over a

[Music]

let us try computing for the magnitude

and direction of vector a

as you may have observed the magnitude

is calculated just like the pythagorean

theorem

substituting the values we get magnitude

of vector

as 6.4 units for its direction

simply get the arc tan of five over four

we get theta as 51.34

let's try another sample problem three

forces act on a point

eight n at zero degrees 9n at 90 degrees

and 10n at 217 degrees what is the net

force

first let us draw the diagram for this

problem so we can easily analyze

for 8 newtons it is at 0 degrees so we

draw it like this

then let us draw 9 newtons which is

directed to 90 degrees

third 10 newtons is at 217 degrees

finally let us draw the resultant

observe that the shaped formed is not a

triangle

not even a square so we cannot use the

pythagorean theorem and the law for

cosines

to solve this let us consider the

summation of the foss's x and y

components

for the summation of the foss's x

component we write f sub x

all magnitudes directed to the right are

positive while all that is directed to

the left will be negative

we write f x as equals to positive 8

plus 0

because the 9 newton force has no x

component

to get fx remember that the position of

of the force 10 newtons is at 217

degrees

now locating the x component we draw a

yellow dashed line and a red dashed line

for the y component

to be able to use sine we need to get

the angle between the hypotenuse and the

y component

subtracting 217 from 270 we get 53

now we can write fx equals 10 sine 53

the summation of fx is 0.013644 newtons

for the summation of fy we write all

magnitudes directed upward as positive

now to get fy we use cosine considering

that the angle is between the adjacent

side and the hypotenuse

for the summation of fy we get 2.9818

now to get the resultant we simply

compute for the square root of the

square of the summation of fx and fy

our resultant r is equals 2.9818 newtons

to determine whether our resultant's

direction is right let us compute for

theta arctan multiplied by fy

over fx we get 89.7378 degrees

[Music]

for your activities answer activity 1 on

page 13

activity 2 on page 14 activity 3 on page

15 and activity 4 on page 16.

that's all for today have a nice day