(RINGKASAN) Materi Vektor | Fisika SMA Kelas 10

Summary

In this educational video, Pak Agung introduces the concept of vectors in physics, specifically for Class 10 students based on the 2013 Curriculum. He covers essential topics like vector and scalar quantities, the significance of vectors in real-life applications (such as GPS), and how to represent vectors graphically and analytically. The video explains trigonometric functions in the context of vectors, methods for determining vector results, and the use of the cosine and sine laws for vector addition. Pak Agung also discusses various methods for solving vector problems, such as graphical (triangle, parallelogram, polygon) and analytical techniques. This lesson provides a comprehensive foundation for understanding vectors and their applications.

Takeaways

• 😀 Vectors are physical quantities with both magnitude and direction, such as velocity, acceleration, and momentum.
• 😀 Scalars are physical quantities with only magnitude, such as mass and time, with no direction involved.
• 😀 Understanding vectors is crucial for applications like GPS, which relies on vector mathematics.
• 😀 Vectors are often represented with an arrow over a capital letter or using bold and italicized letters.
• 😀 Trigonometry is essential when working with vectors, especially with special angles (30°, 45°, 60°) and their sine, cosine, and tangent values.
• 😀 To memorize special angles, a trick is to remember the sequence of values (0, 1/2, √2/2, √3/2, 1) and reverse them for cosine.
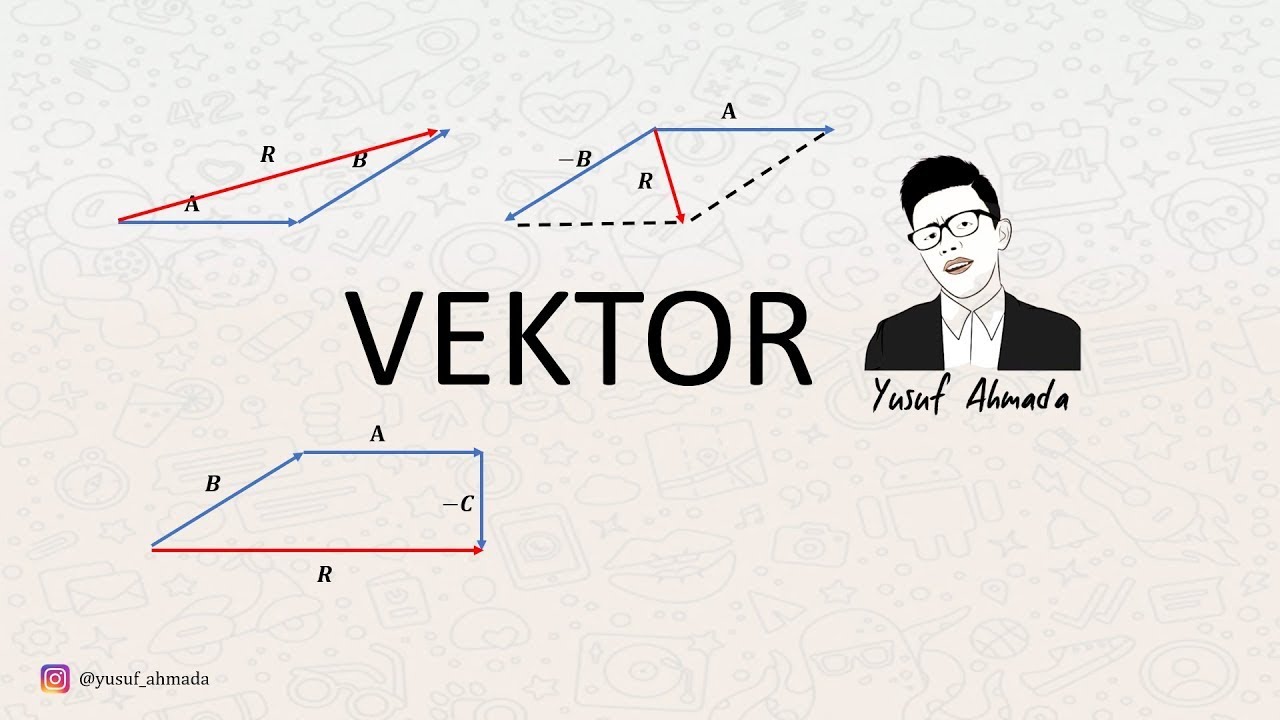
• 😀 The geometric methods to find vector results include the triangle method (for two vectors), parallelogram method (for two vectors), and polygon method (for more than two vectors).
• 😀 The analytical methods involve calculating the vector result using formulas such as the law of cosines and sines for two vectors or more.
• 😀 Vector components can be broken down into x and y components using trigonometric functions like sine and cosine based on the angle relative to the axes.
• 😀 When calculating the resultant of multiple vectors, you decompose each vector into its components along the x and y axes and then sum them to find the overall result.

Q & A

What is the difference between vector quantities and scalar quantities?

Vector quantities have both magnitude and direction, such as velocity, acceleration, and momentum. Scalar quantities only have magnitude, with no direction, such as mass, time, and temperature.

What is the symbol used to represent a vector?

A vector is typically represented by a capital letter with an arrow on top (e.g., v⃗) or sometimes with bold or italic capital letters to indicate its vector nature.

Why is learning vectors important in physics?

Understanding vectors is crucial in physics because they are fundamental in describing quantities like displacement, force, and velocity, and they are used in various applications such as GPS systems.

What are the three methods for finding the resultant of two vectors geometrically?

The three methods for determining the resultant of two vectors geometrically are: the triangle method, the parallelogram method, and the polygon method.

How do the triangle and parallelogram methods differ when determining the resultant of two vectors?

In the triangle method, the vectors are drawn such that the tail of one vector meets the head of the other, and the resultant is the vector from the tail of the first to the head of the second. In the parallelogram method, both vectors are drawn from the same origin, forming a parallelogram, and the resultant is the diagonal of this parallelogram.

What is the analytical method for finding the resultant of vectors?

The analytical method involves breaking each vector into its horizontal (x) and vertical (y) components, summing these components separately, and then using Pythagoras' theorem to find the resultant.

How do you apply the law of cosines to find the resultant of two vectors?

To apply the law of cosines, use the formula R = √(F1² + F2² + 2F1F2cos(θ)), where F1 and F2 are the magnitudes of the vectors and θ is the angle between them.

What is the difference between the sine and cosine rule when resolving vectors?

The sine rule is used when you know the angle opposite a vector component, and the cosine rule is used when you know the angle between the two vectors being combined. The sine rule is often used for finding angles, while the cosine rule helps find the resultant magnitude.

What does it mean to decompose a vector, and how do you do it?

Decomposing a vector means breaking it down into its components along the x and y axes. For example, a vector at an angle is decomposed into two parts: one along the x-axis (F cos(θ)) and one along the y-axis (F sin(θ)).

How do you determine the angle of the resultant vector after decomposing multiple vectors?

To find the angle of the resultant vector, use the arctangent function: θ = tan⁻¹(Sum of y-components / Sum of x-components), which gives the direction of the resultant relative to the x-axis.