Proof: perpendicular lines have negative reciprocal slope | High School Math | Khan Academy
Summary
TLDRThis video uses geometric arguments to demonstrate that the slopes of perpendicular lines are negative reciprocals of each other. By constructing lines and points, the presenter shows that the slope of one line can be found by comparing changes in Y and X coordinates, and then proves the relationship between the slopes of perpendicular lines by establishing the similarity of two triangles.
Takeaways
- 📚 The video aims to prove that the slopes of perpendicular lines are negative reciprocals of each other using geometric arguments.
- 📐 Lines L and M are assumed to be perpendicular, intersecting at a right angle.
- 📏 A horizontal line is constructed to intersect at point A, and vertical lines are dropped to create additional points B, C, D, and E.
- 🔍 The slope of line L is determined by the change in Y (length of CB) over the change in X (length of BA).
- 🔍 The slope of line M is determined by the negative change in Y (length of DE) over the change in X (length of AD), reflecting the downward direction.
- 🔄 The video establishes that triangles CBA and ADE are similar by showing that their corresponding angles are equal.
- 🔄 The similarity of the triangles is used to show that the ratio of corresponding sides (CB/BA and AD/DE) is the same.
- 🔄 The slope of line L is shown to be the reciprocal of the slope of line M, with the negative sign indicating the perpendicular relationship.
- 🔄 The negative reciprocal relationship is demonstrated by comparing the ratios of corresponding sides in the similar triangles.
- 📉 The video concludes by confirming that if lines L and M are perpendicular, the slope of L is the negative reciprocal of the slope of M.
Q & A
What is the main purpose of the video?
-The main purpose of the video is to use geometric arguments to prove that the slopes of perpendicular lines are negative reciprocals of each other.
What assumption is made about lines L and M at the beginning of the video?
-The assumption made is that lines L and M are perpendicular to each other, intersecting at a right angle.
How does the video construct a geometric argument to prove the relationship between the slopes of perpendicular lines?
-The video constructs a geometric argument by drawing lines and points to form triangles and then demonstrating the similarity of these triangles to establish the relationship between the slopes.
What is the significance of the horizontal line drawn in the video?
-The horizontal line is significant as it intersects the perpendicular lines at point A, setting the stage for further geometric constructions and arguments.
Why are vertical lines dropped in the video?
-Vertical lines are dropped to create right angles and to form triangles that will be used to prove the relationship between the slopes of perpendicular lines.
What are the points labeled B, C, D, and E in the video?
-Points B, C, D, and E are labeled to identify specific locations on the lines and to facilitate the discussion of the slopes and the geometric argument.
How is the slope of line L determined in the video?
-The slope of line L is determined by considering it as the line connecting point C to point A (CA) and calculating the change in Y (length of CB) over the change in X (length of BA).
What is the slope of line M in relation to the slope of line L?
-The slope of line M is the negative reciprocal of the slope of line L, which is derived from the geometric argument involving similar triangles.
How are the triangles CBA and ADE shown to be similar in the video?
-The triangles CBA and ADE are shown to be similar by demonstrating that their corresponding interior angles are the same, using the fact that the sum of the angles in a triangle is 180 degrees.
What conclusion is reached by establishing the similarity of triangles CBA and ADE?
-By establishing the similarity of triangles CBA and ADE, it is concluded that the ratio of corresponding sides is the same, which leads to the proof that the slope of L is the negative reciprocal of the slope of M.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Writing Equations of Parallel and Perpendicular Lines

Writing Equation of a Line
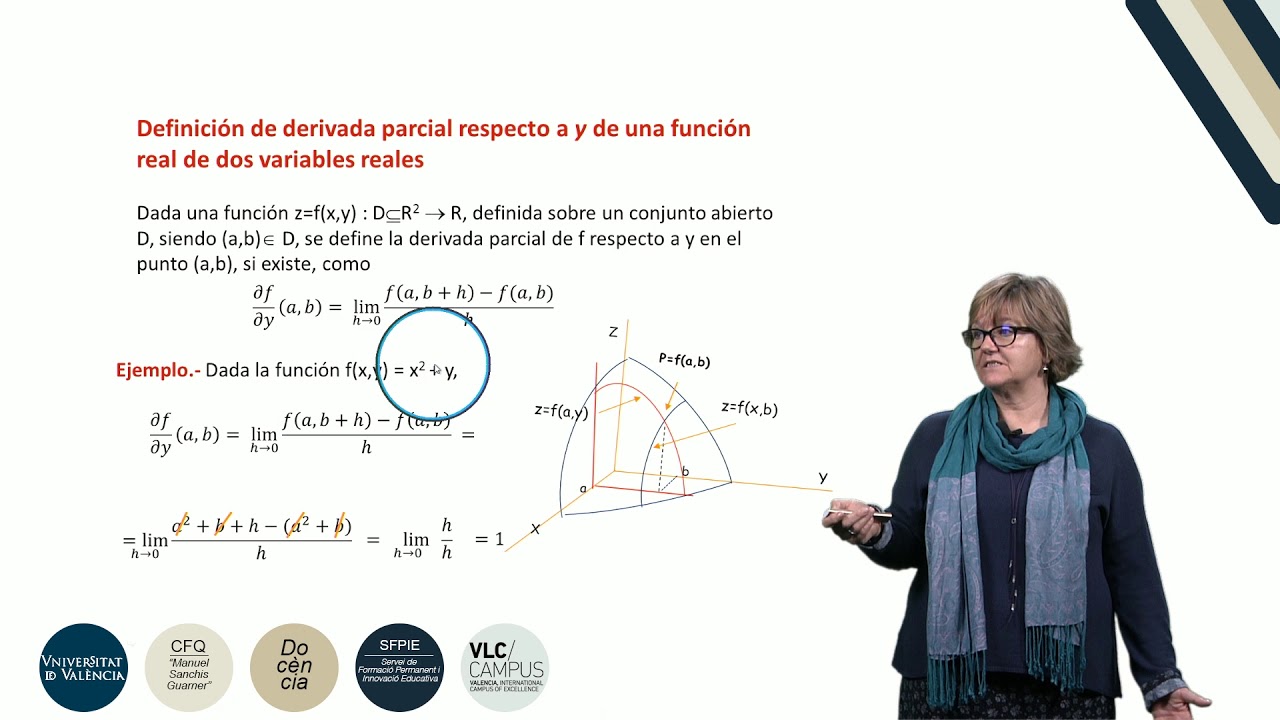
Derivadas parciales. Interpretación geométrica

Slope, Line and Angle Between Two Lines |Analytic Geometry|

Pengertian Kemiringan Hal 239-243 Bab 5 Persamaan Garis Lurus Kelas 8 Kurikulum Merdeka Belajar

Bangun Datar [Part 3] - Melukis Garis, Sudut, dan Bangun Datar
5.0 / 5 (0 votes)