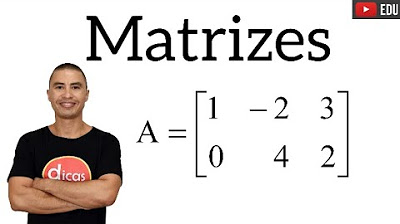Matriks Matematika Wajib Kelas 11 Bagian 1 - Pengenalan Matriks

Summary

In this video, Daniel Dayani introduces the concept of matrices, covering definitions, matrix orders, types of matrices, transposes, and matrix equality. He explains matrices as a collection of numbers or symbols arranged in rows and columns, and distinguishes between rows and columns. The video also explores different matrix types like row, column, rectangular, and square matrices, as well as special types such as diagonal, identity, and triangular matrices. The session concludes with examples and exercises to reinforce learning. Viewers can download the lesson in PDF format from the video description.

Takeaways

• 📊 Matrices consist of numbers, symbols, or expressions arranged in rows and columns, often enclosed by brackets.
• 🔢 Elements within matrices are referred to as entries and can be denoted using subscripts based on their row and column positions.
• 📏 The order of a matrix is defined by the number of rows and columns, expressed as 'rows x columns'.
• 📝 Matrices can be classified by their structure: row matrices have one row, column matrices have one column, rectangular matrices have different numbers of rows and columns, and square matrices have the same number of rows and columns.
• 🔄 Transpose of a matrix is obtained by swapping its rows and columns.
• 🔳 Diagonal matrices have non-zero elements only on their main diagonal, with other elements being zero.
• 1️⃣ Identity matrices are square matrices with ones on the main diagonal and zeros elsewhere.
• 🔺 Upper triangular matrices have all elements below the main diagonal as zero, while lower triangular matrices have all elements above the main diagonal as zero.
• ♻️ Symmetric matrices are those where the matrix is equal to its transpose.
• ➕ Matrices are considered equal if they have the same order and identical elements in corresponding positions.

Q & A

What is a matrix?

A matrix is a collection of numbers, symbols, or expressions arranged in rows and columns to form a rectangular array, typically enclosed in brackets or parentheses.

How are elements within a matrix referred to?

Elements within a matrix are referred to as entries or elements of the matrix. For example, in matrix A, an element in the 2nd row and 3rd column is written as A23.

What defines the order of a matrix?

The order of a matrix is defined by the number of rows (m) and columns (n) it has, written as m x n. For example, a matrix with 2 rows and 3 columns has an order of 2 x 3.

What is a row matrix?

A row matrix is a matrix that has only one row, regardless of the number of columns. For example, [1, 2, 3] is a row matrix with one row and three columns.

What is a column matrix?

A column matrix is a matrix that has only one column, regardless of the number of rows. For example, [[1], [2], [3]] is a column matrix with three rows and one column.

What is a rectangular matrix?

A rectangular matrix is a matrix where the number of rows and columns are different, forming a rectangle. For example, a matrix with 2 rows and 3 columns is a rectangular matrix.

What is a square matrix?

A square matrix is a matrix where the number of rows is equal to the number of columns, forming a square. For example, a 3 x 3 matrix is a square matrix.

What is the main diagonal of a square matrix?

The main diagonal (or principal diagonal) of a square matrix consists of elements that run from the top-left to the bottom-right corner. For example, in a 3 x 3 matrix, the main diagonal elements could be [1, 4, 7].

What is a zero matrix?

A zero matrix is a matrix in which all the elements are zero. It is denoted by O and can have any order. For example, a 2 x 2 zero matrix is [[0, 0], [0, 0]].

What is a diagonal matrix?

A diagonal matrix is a square matrix where all the elements outside the main diagonal are zero, but the elements on the main diagonal can be any value. For example, [[1, 0, 0], [0, 2, 0], [0, 0, 3]] is a diagonal matrix.

What is an identity matrix?

An identity matrix is a square matrix where all the elements on the main diagonal are 1, and all other elements are zero. It acts as a multiplicative identity in matrix multiplication. For example, a 2 x 2 identity matrix is [[1, 0], [0, 1]].

What is a triangular matrix?

A triangular matrix is a square matrix where all the elements above (upper triangular) or below (lower triangular) the main diagonal are zero. For example, an upper triangular matrix has zeros below the main diagonal.

What does the transpose of a matrix mean?

The transpose of a matrix is obtained by swapping its rows with its columns. For example, the transpose of a matrix A with elements [[1, 2], [3, 4]] is [[1, 3], [2, 4]].

What is a symmetric matrix?

A symmetric matrix is a square matrix that is equal to its transpose. For example, if matrix A is [[1, 2], [2, 3]], it is symmetric because A equals A^T.

When are two matrices considered equal?

Two matrices are considered equal if they have the same order and their corresponding elements are identical. For example, matrices A and B are equal if A[i][j] = B[i][j] for all i and j.

Outlines

00:00

📚 Introduction to Matrices

Daniel Dayani welcomes viewers and introduces the topic of matrices, explaining that this video is the first in a series. He outlines the content to be covered: definitions, orders, types, transposition, and matrix equality. He also mentions that the material is available for download in PDF format.

05:02

🧮 Understanding Matrices

Daniel defines a matrix as a collection of numbers, symbols, or expressions arranged in rows and columns, forming a rectangle or square enclosed by brackets. He explains the terms 'rows' and 'columns,' emphasizing their orientation (horizontal for rows, vertical for columns). The concept of matrix elements and their notation using capital and lowercase letters is also introduced.

10:02

🔢 Matrix Order and Types

The order of a matrix, which is determined by the number of rows and columns, is explained with examples. Daniel distinguishes between different types of matrices based on their rows and columns, including row matrices, column matrices, rectangular matrices, and square matrices. The concept of the main diagonal and secondary diagonal in square matrices is also covered.

15:04

🔷 Matrix Patterns and Types

Daniel discusses matrices based on element patterns. He explains zero matrices, where all elements are zero, and diagonal matrices, where only the main diagonal elements are non-zero. Identity matrices, with ones on the main diagonal and zeros elsewhere, are described. The segment concludes with triangular matrices (upper and lower), where elements above or below the main diagonal are zero.

20:05

🔄 Matrix Transposition and Symmetry

Matrix transposition, which involves swapping rows with columns, is demonstrated with examples. Daniel explains that a matrix is symmetric if it equals its transpose. He also discusses the equality of matrices, emphasizing that matrices are equal if they have the same order and identical elements in corresponding positions.

Keywords

💡Matriks

A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. In the video, the concept of a matrix is introduced as the main topic, explaining its definition, elements, and notation.

💡Ordo Matriks

The order of a matrix is defined by the number of rows (m) and columns (n) it contains, denoted as m x n. The video details how to determine the order by counting the rows and columns, emphasizing the importance of correct notation.

💡Elemen Matriks

Matrix elements are the individual numbers, symbols, or expressions within the matrix, enclosed by brackets. The video explains how elements are identified and notated, such as aij indicating the element in the ith row and jth column.

💡Baris dan Kolom

Rows and columns in a matrix refer to the horizontal and vertical lines of elements, respectively. The video clarifies their distinction and importance in understanding matrix structure and operations.

💡Transpose Matriks

The transpose of a matrix is obtained by swapping its rows with its columns. In the video, this concept is demonstrated with examples, showing how to convert a given matrix into its transpose.

💡Matriks Identitas

An identity matrix is a square matrix with ones on the diagonal and zeros elsewhere. The video explains this concept and illustrates it with examples, highlighting its unique properties and notation.

💡Diagonal Utama

The main diagonal of a matrix runs from the top left to the bottom right, containing elements where the row and column indices are equal. The video discusses the significance of the main diagonal in various matrix types and operations.

💡Matriks Nol

A zero matrix is one where all elements are zero. The video introduces this type of matrix, explaining its notation and providing examples to show its structure.

💡Matriks Simetris

A symmetric matrix is equal to its transpose, meaning aij = aji for all elements. The video discusses this property and provides examples to illustrate when a matrix is symmetric.

💡Matriks Segitiga

Triangular matrices have all elements either above or below the main diagonal equal to zero. The video differentiates between upper and lower triangular matrices, explaining their properties and uses with examples.

Highlights

Introduction to matrices, including definition and examples of matrices, elements, rows, and columns.

Explanation of matrix notation, using capital letters for matrices and lowercase for elements, with examples.

Definition and explanation of the order of a matrix (m x n), illustrating how to determine the number of rows and columns.

Types of matrices based on the number of rows and columns, including row matrix, column matrix, rectangular matrix, and square matrix.

Detailed description of special types of matrices: diagonal matrix, identity matrix, and triangular matrices (upper and lower).

Understanding matrix transpose: how to interchange rows and columns, with step-by-step examples.

Definition of symmetric matrices, where a matrix is equal to its transpose.

Criteria for matrix equality: two matrices are equal if they have the same order and corresponding elements are equal.

Worked examples to illustrate matrix properties, including finding the sum of diagonal elements.

Explanation of identity matrices and how to recognize them, including examples and non-examples.

Practice problem on finding the values of elements in a given diagonal matrix.

Identification and properties of triangular matrices, both upper and lower triangular matrices.

Worked example to find the transpose of a given matrix, demonstrating the process of converting rows to columns.

Practice problem involving matrix equality and solving for unknown elements in matrices.

Conclusion of the video with a preview of upcoming topics on matrix operations such as addition, subtraction, and multiplication.

Transcripts

Assalamualaikum warahmatullahi

wabarakatuh ketemu lagi dengan saya

Daniel dayani di channel Redline pada

video ini kita akan belajar materi

matriks materi matriks akan saya bagi ke

dalam beberapa video terpisah ini adalah

video bagian pertama pada video ini kita

akan belajar pengertian matriks ordo

matriks jenis-jenis matriks transpose

matriks dan kesamaan dua matriks materi

yang saya sampaikan pada video ini bisa

teman-teman download bentuk PDF nya

linknya silahkan lihat di deskripsi

video ini Oke sekarang kita akan belajar

materi tentang matriks kita mulai dari

pengertian matriks dulu ya Nah ini

pengertian matriks matriks adalah

kumpulan bilangan simbol

ekspresi berbentuk persegi atau persegi

panjang yang disusun menurut baris dan

kolom lebih jelasnya perhatikan contoh

berikut nama trik itu seperti ini

temen-temen ya jadi didalamnya ini ada

sekumpulan bilangan atau bisa simbol

bisa ekspresi yang kita susun menjadi

persegi panjang atau bisa juga persegi

kemudian dibatasi oleh tanda kurung

seperti ini tanda kurung ya bisa tanda

kurung biasa ya Atau bisa juga

teman-teman menggunakan tanda kurung

siku seperti contoh ini walaupun

Hai nah yang didalamnya ekspresi yang

didalamnya atau bilangan atau simbol

yang ada didalam tanda kurung ini ini

disebut sebagai elemen-elemen matriks

atau entri Eh nah 2104 negatif 27 ini

elemen-elemen matriks yang ini oke nah

seperti di pengertian disinikan disusun

menurut baris dan kolom teman-teman

harus paham mana yang dimaksud dengan

baris mana yang dimaksud dengan kolom

misalnya perhatikan matriks ini yang

disebut dengan dari situ elemen yang

horizontal yang datar 210 ini berarti

baris pertama

Hai naik yang bawah ini baris kedua

ingat baris itu adalah yang datar atau

horizontal sementara yang vertikal ini

disebut sebagai kolom ini kolom pertama

ini kolom kedua dan ini kolom ketiga

jelas ya dari situ yang horizontal atau

yang datar dan kolom itu yang tegak atau

yang vertikal oke sekarang notasi

matriks matriks dinyatakan dengan huruf

kapital dan elemen-elemennya dinyatakan

dengan huruf non kapital huruf kapital

itu huruf besar non Capital yaitu huruf

kecil ya jika matriks A adalah sebuah

matriks aij nah ini berarti elemen IG

menyatakan elemen yang terletak pada

baris ke I dan kolom ke J jadi nama

matrik kita gunakan dengan huruf kapital

dan elemennya kita gunakan huruf non

kapital sebagai contoh

Hai misalkan ini adalah matriks A kita

lihat di sini kita gunakan huruf kapital

ini nama matriksnya nah ini adalah

elemen-elemennya elemen pada baris ke-2

kolom ketiga Nah kita tulis A23 artinya

ini elemen matriks A Ya A kecil ini

artinya elemen matriks A 2 3 ini artinya

baris ke-2 kolom ketiga nah teman-teman

jangan baca 23 ya ini baca 1123 sebagai

artinya baris ke-2 kolom ketiga lihat

baris kedua yang mana baris itu yang

horizontal berlian sebelah sini ya ini

baris ke-2 kolom ketiga nah ini kolom

itu yang vertikal kolom ketiga baris

ke-2 kolom ketiga albertina sebelah sini

kan jadi A23 itu adalah negatif

Hai elemen pada baris ketiga kolom ke-1

a31 ya elemen baris ketiga kolom ke-1

baris ketiga itu yang ini 911 kolom ke-1

kolom ke-1 yang vertikal yang pertama

nah ini Oh berarti nilainya adalah a31

itu 9 jelasnya

Hai Nah sekarang ada istilah ordo

matriks ya di matriks ada yang sebut

dengan ordo jika suatu matriks A terdiri

dari ember s&n kolom maka m * n

menyatakan ukuran atau ordo dari matriks

A yang disebut dengan ordo itu adalah

ukuran matriks yang menyatakan banyaknya

baris dan kolom teman-teman eh jadi

teman-teman harus paham dulu mana baris

mana kolom maka ordonya itu banyaknya

baris kali banyaknya kolom hati-hati

kebalik ingat baris dulu kali kolom

contoh

Hai nah ini matriks A ada berapa

baris-baris itu yang horizontal yang

datar oh di sini ada dua baris nih Ada

berapa kolom ada tiga kolom-kolom

pertama uang kedua dan kolom ketiga

berarti ordo matriks ini adalah dua kali

tiga karena ada dua baris 3 kolom

ditulis A23 sekali lagi hati-hati jangan

kebalik ya kalau tiga kali dua itu

artinya beda lagi bentuk matriksnya beda

lagi jadi Posisinya itu harus baris dulu

banyak baris dulu lalu kali banyaknya

kolom Oke contoh lagi misalkan ini

adalah matriks B ada berapa baris ada

tiga baris ya satu baris kedua baris

ke-3 ada satu kolom berarti ordo matriks

ini adalah tiga kali satu karena

memiliki tiga baris dan Suatu kolom

jelas ya oke selain kita pelajari

jenis-jenis matriksnya ini saya

golongkan menjadi

sebagian yang pertama jenis matriks

berdasarkan banyaknya baris dan kolom

dan yang kedua nanti kita pelajari jenis

matriks berdasarkan polanya Nah kita

pelajari dulu yang pertama jenis matriks

berdasarkan banyaknya baris dan kolom

yang pertama ada matriks baris matriks

baris itu matriks yang memiliki satu

baris teman-teman jadi kolomnya bisa

berapapun yang penting banyaknya baris

yaitu hanya satu sebagai contoh nah ini

matriks baris kena bahkan abadinya cuma

ada satu satu baris kolom ya di sini ada

tiga Nah contoh lagi ini juga matriks

baris banyaknya baris cuma satu ini

kolomnya ada dua jadi enggak berapapun

kolomnya yang penting kalau barisnya

cuma satu itu dikatakan sebagai matriks

baris Nah yang kedua ada matriks kolom

sebaliknya kalau matriks kolom itu

banyaknya kolomnya yang yang hanya satu

barisnya bisa berapa pun

Hai sebagai contoh ini matriks A ada

tiga baris tapi kolomnya satu maka ini

dikatakan sebagai matriks kolom matriks

B ada dua baris 1 kolom ini juga sama

matriks kolom oke nah sekarang yang

disebut dengan matriks persegi panjang

ya matriks persegi panjang itu matriks

yang memiliki jumlah baris dan kolom

berbeda sebagai contoh nah ini matriks A

the melihat bentuknya dia persegipanjang

baris dan kolomnya berbeda kemudian

matriks B ini juga sama

Hai baris dan kolomnya berbeda bentuknya

juga berupa persegi panjang jadi

dikatakan sebagai matriks persegi

panjang kemudian yang keempat matriks

persegi Nah kalau matriks persegi itu

banyaknya baris dan kolomnya sama

sebagai contoh ini matriks A Udo nyatuin

tiga kali 33 baris 3 kolom lihat ini

berbentuk persegi karena banyaknya baris

dan kolom sama kemudian matriks B ini

ordonya dua kali dua baris dan kolomnya

sama ini juga dikatakan sebagai matriks

persegi nah pada matriks persegi ada

yang disebut dengan diagonal utama eh

diagonal utama itu yang sebelah sini

temen-temen nah ini dikatakan sebagai

diagonal utama 141 lalu diagonal yang

satu lagi yang sebelah sini ya kita

Hai ini dikatakan sebagai diagonal

sekunder atau diagonal samping coba pada

matriks B diagonal utamanya mana 1 dan 3

diagonal sampingnya atau diagonal

sekundernya dua dan nol nah diagonal

utama ini kalau kita jumlahkan

elemen-elemennya jumlahnya itu dikatakan

sebagai fresh misalkan it resembles apa

Satu tambah 4 + 1 kobra T6 disini trace

nya satu tambah tiga karena diagonal

utamanya 1 dan 3 berarti 4ws nya

jelasnya Nah itu jenis-jenis matriks

berdasarkan banyaknya baris dan kolom

Oke seorang kita pelajari jenis-jenis

matriks berdasarkan pola

elemen-elemennya yang pertama ada yang

disebut sebagai matriks nol matriks nol

itu matriks yang semua elemennya

bernilai nol jadi kita enggak melihat

berapapun ordonya asalkan semua elemen

yang bernilai nol itu dikatakan sebagai

matriks nol penamaannya itu

anda akan huruf Oka vital sebagai contoh

O2 kali tiga ini matriks nol yang

berordo 2 * 3/2 baris 3 kolom

teman-teman lihat ini elemennya nol

semua contoh lagi ini matriks nol yang

ordonya dua kali dua dua baris 2 kolom

oke yang kedua ada yang dikatakan

sebagai matriks diagonal matriks

diagonal itu matriks persegi yeah jadi

ordonya itu harus sama baris dan

kolomnya sementara elemen pada diagonal

utama tidak semua nol dengan elemen

lainnya 0contoh

Hai nah ini matriks diagonal itu harus

matriks persegi Nah Lihat diagonal utama

ini enggak boleh nol semua ya ini enggak

boleh no semua jadi kalau salah satu

atau dua 02 entry no itu ga masalah yang

penting enggak boleh semuanya nol

sementara entri atau elemen lainnya itu

nol semua maka itu dikatakan sebagai

matriks diagonal contoh lagi Nah

teman-teman Lihat diagonal utamanya 300

nah ini ada sesuatu yang bukan nol maka

ini dikatakan sebagai matriks diagonal

elemen lainnya itu nol semua Gan

Hai nah berikutnya yang ketiga ada yang

disebut dengan matriks identitas nah ini

juga sama matriks persegi tapi diagonal

utama kalau identitas itu harus bernilai

satu semua elemen lainnya bernilai nol

contoh ini identitas matriks ordo 3 kali

3 lihat diagonal utamanya kan satu semua

nah ini identitas matriks ordo 2 * dua

kita lihat diagonal utamanya ini harus

satu semua elemen lainnya selain

diagonal utama itu bernilai 0 maka

dikatakan sebagai matriks identitas

Hai kemudian yang keempat ada yang

disebut sebagai matriks segitiga nah

matriks segitiga itu jika elemen dibawah

atau diatas diagonal utama semuanya nol

ya mati segitiga ada 2 jenis yang

pertama ada matriks segitiga atas itu

disimbolkan atau diberi nama dengan muka

vital nah matriks segitiga atas yang

bukan nonya bagian atas sementara yang

di bawah diagonal utama itu semuanya nol

sebagai contoh Nah teman-teman lihat

kalau segitiga atas itu di bawah

diagonal utama sebaliknya yang atas itu

kalau di bawah diagonal utama itu

semuanya nol nah ini dibawa dia begini

kan diagonal utama yang dibawahnya itik

ini nol semua jadi yang kita buat

segitiga itu yang bukan nolnya Nah ini

nih segitiganya maka ini dikatakan

segitiga atas

Hai Nah yang kedua matriks segitiga

bawah biasanya diberi nama El Capital

contohnya Ini kebalikannya ya kalau

segitiga bawah berarti yang di atas

diagonal utamanya yang nol ya contoh nah

ini diagonal utama lihat bagian atasnya

kan nol berarti yang kita buat segitiga

itu yang bukan nonya nah ini segitiganya

Jadi nih disebut sebagai matriks

segitiga bawah oke itu adalah

jenis-jenis matriks berdasarkan pola

elemen-elemennya Oke seorang kita

pelajari transpose matriks nah secara

sederhana yang dikatakan sebagai

transpose matrik itu kita menukar antara

elemen baris dengan elemen kolom sebagai

contoh misalkan di sini kita punya

matriks A ini matriks ordo 3 kali 3 ya

kita akan mencari transposenya A

transpose itu disimbolkan dengan ^ the

Ok Jadi kalo ada a pangkat b berarti ini

transpose dari matriks A caranya

menukar antara elemen baris dengan

elemen kolom atau sebaliknya kolom

dengan baris juga enggak masalah

teman-teman lihat baris pertama 1 2 dan

3 ini kan baris kita tulis kalau

transposenya kita tulis menjadi kolom 1

2 dan 3 ini jadi baris pertama kita

jadikan sebagai kolom pertama baris

kedua 345 kalau transposenya kita

jadikan kolom ke dua tiga empat lima

Hai dan baris ketiga 211 ini kita

jadikan kolom ketiga jelas ya kita

menukar atau mengubah baris menjadi

kolom Nah itu dikatakan sebagai

transpose matriks

Hai contoh lagi ini matriks A

Hai 2141 45453 kita akan mencari

transposenya kita lihat baris pertama

214 ini kita jadikan kolom pertama 214

baris kedua 145 kita jadikan kolom kedua

145 dan baris ketiga 453 ini kita

jadikan kolom ketiga 4536 ini adalah A

transpose atau matriks transpose dari

matriks A Nah kalau teman-teman lihat

antara kalau contoh kedua ini matriks A

dengan A transpose itu nilainya sama kan

kalau main itu sama2 14214 145 145 4534

53 Nah kalau terjadi kasus seperti ini

ternyata matriks a = a transpose ini

dikatakan sebagai matriks simetris

Hai ke ini sedikit typo ya matriks A

disebut sebagai matriks simetris kalau

ternyata hanya dia = a transpose kalau

dicontoh satu itu membedakan batu Ini

bukan matriks simetris jelas ya Nah

sekarang kita bahas kesamaan dua matriks

matriks itu dikatakan sama jika ordo

yang sama dan elemen-elemen yang

letaknya sama itu bernilai sama

contohnya

Hai misalkan kita punya matriks A dan

matriks B ini matriks hanya setengah 059

sementara matic sebaiknya Sin p60 akar

2534 dua Nah ini matriks A dengan b itu

matriks yang sama a = b Kenapa karena

yang elemen letaknya sama misalkan ini

setengah ini kan elemen baris 1 kolom

satu Disini by itu elemen satu elemen

baris 1 kolom satu itu sama Sin phi per

enam ini adalah Shin eh Sin 30°

a Sin 30° Sin 30° itu kan setengah juga

jadi ini nilainya sama setengah ini

baris pertama kolom ke-20 kan sama juga

kemudian ini baris ke-2 kolom pertama

lima ini akan 25 Berapa akar 25 ya lima

juga ya Enggak ini baris ke-2 kolom

ke-29 ini tiga kuadrat berapa 9 juga

jadi ini asam aja dengan B karena

nilainya sama

Hai Oke sekarang kita coba bahas

beberapa contoh soal latihan kita mulai

dari soal pertama soalnya seperti ini

jumlah elemen-elemen diagonal diagonal

utama matriks Peni matriksnya kita akan

menjadi jumlah elemen diagonal utama

yang disebut dengan diagonal utama tuh

bagian sini ya lima negatif 10 kemudian

satu Nah ini pilihannya jadi kita

tinggal jumlahkan aja ingat diagonal

utama itu sebelah sini berarti 5

ditambah negatif 10 kemudian ditambah 15

ditambah negatif 10 negatif 5 negatif 5

ditambah satu itu negatif 4 jadi

jawabannya adalah they kita lanjut ke

soal kedua

Hai matriks Berikut yang merupakan

matriks identitas nah yang mana

identitas itu matriks persegi yang

diagonal utamanya satu ya Nah ini bukan

identitas lihat diagonal utamanya di

saya 10 B juga ini bukan identitas

diagonal utamanya juga 10 yang c juga

bukan nah ini diagonal samping satunya

yang bernilai satu jadi ini bukan ya

yang Dek Ini matrik identitas karena

diagonal utamanya bernilai satu

sementara elemen lainnya itu bernilai

nol jadi ini jawabannya adalah D Serang

kita bahas soal ketiga penghasilan

Hai diketahui matriks ini adalah matriks

diagonal nilai a b c berturut-turut

adalah nah ini matriks diagonal ingat

matriks diagonal itu yang diagonal utama

itu tidak bernilai nol semua sementara

elemen lainnya bernilai nol jadi yang

ini Ini kan elemen lain selain diagonal

utama dia harus bernilai 0 b min 1 = 0

berarti bb-nya = 1 kemudian Eh ini aja

dulu ya a + b Mbak harus bernilai nol

juga goyang Bukan nol itu diagonal utama

ya jadi dari sini kita dapat Oh ya

Banyak kita ganti aja dengan satu ya A +

1 = 0 makanya adalah negatif satu

Kemudian dari sini

G2 a + c juga bernilai nol kita dapat

aanya itu negatif 12 kali aq3 Nti aanya

negatif Satu Ditambah c = 0 2 kali

negatif satu negatif 2 ditambah c = 0

maka c-nya = positif dua Nah Disini yang

ditayangkan adalah nilai a b c

berturut-turut berarti dari Aduh lu yah

negatif 1B nya satu c-nya 2 negatif 1 1

dan 2 jawabannya adalah C kita lanjut ke

contoh keempat soal keempat diketahui

matriks segitiga atas Eh ini matriks

segitiga atas nilai x yang memenuhi

ingat kalau matriks segitiga atas

berarti yang bawahnya ini bernilai nol

semoga teman-teman nah bagian sini ini

bernilai nol semua eh jadi y dikurangi

satu di harus bernilai 0 maka ianya satu

oke ini juga sama harus bernilai nol

x-men

4 y = 0 y nya kan udah dapet satu jadi x

dikurangi empat kali satu sama dengan

nol x dikurangi 4 sama dengan nol maka

exim berapa esnya adalah positif empat

ada nggak jawabannya adalah a Oke song

kita bahas contoh soal kelima ini sangat

terakhir yang akan kita bahas pada video

kali ini diketahui matriks A ini matriks

hanya dan ini matriks b nya Jika a = b

maka a transpose = Nah kita gunakan

kesamaan dua buah matriks ingat dua buah

matriks itu dikatakan sama jika ordonya

sama nih ya ini matriks A dan B Itu

ordonya sama yaitu tiga baris 2 kolom

ini juga sama tiga baris 2 kolom 1

Hai dan yang kedua itu dikarenakan sama

jika elemen yang letaknya sama nilainya

sama jadi baris ke-1 persatu ini satu

ini juga sama satu ini empat ini juga

sama empat ini negatif 5 ini juga sama

ya enggak nah Disini yang ditanyakan

adalah a transpose berarti kita harus

tahu dulu ini elemen yaitu berapa aja

Nah untuk dapat nilai ini kita harus

tahu dulu nilai a ini juga sama jadi

target kita akan mencari nilai Anya dulu

ya kita gunakan kesamaan dua buah

matriks pernah kita gunakan bagian ini

dulu kenapa bagian ini karena

variabelnya cuma satu ya

Ayo kita dapat B Min 4

Hai baris ketiga kolom pertama nilainya

sama dengan yang ini ini juga sama baris

ketiga kolom pertama negatif 9 jadi

bb-nya berapa negatif 9 ditambah empat

negatif 5 Nah sekarang kita akan mencari

nilai

Hai milik aq3 gunakan saya pakai yang

ini aja ya oke 5A + 1 = 6 dikurangi

BBnya kita udah dapet ya 5A plus satu =

6 dikurangi b nya kita ganti dengan

negatif 5 jadi 5A + 1 = 6 dikurangi

negatif 5 itu 11 jadi lima A = 11

dikurangi satu 10 makanya Berapa 10

dibagi lima hanya itu dua jadi nih nilai

matriks A elemennya ini bisa kita

lengkapi

Hai saya 2/3 berapa hanya ganti aja

dengan dua dua kali 244 plus 37

Hai nah ini 5A tambah 1 sama Anya ganti

dengan 25 kali 2-10 10 plus satu kau ini

nilainya 11 keyna ini pilihannya jadi

matriks hanya tak

ini adalah satu 7174 negatif

Hai kemudian negatif 9 11

Hai Nah sekarang kita akan mencari

aturan foxnya Ingatkan pos itu merubah

baris jadi kolom dan kolom jadi berrys

jadi baris pertama 17 kita jadikan kolom

pertama 17 baris kedua 4 negatif 5 ini

jadi kolom ke-24 negatif 5 dan baris

ketiga negatif 9 11 ini jadikan kolom

ketiga negatif 9-11 ada enggak 14

negatif 97 negatif 5 11 yang Dek Ya ini

jawabannya Oke sampai sini dulu video

pertama untuk materi matriks video

berikutnya bagian kedua Insyaallah kita

akan belajar operasi matriks penjumlahan

pengurangan dan perkalian

Assalamualaikum warahmatullahi

wabarakatuh

hai hai