Vektor (Definisi Vektor, Vektor Posisi, & Panjang Vektor) - Matematika Kelas 10 - Quipper Video

Summary

This video tutorial introduces the concept of vectors, explaining their definition as line segments with both magnitude and direction. It covers key topics such as vector notation, position and non-position vectors, and how to calculate vector length using the Pythagorean theorem. The lesson includes practical examples, like expressing vectors in component form and calculating their magnitude in both 2D and 3D spaces. The teaching style is casual, aiming to engage students while explaining the foundational concepts of vectors clearly and understandably.

Takeaways

• 😀 Vectors are line segments with both magnitude (length) and direction, crucial in various fields like physics, especially for concepts like acceleration, speed, and electric current.
• 😀 A vector's direction and magnitude can be represented graphically using a Cartesian coordinate system, with points denoted by coordinates (x, y).
• 😀 The notation for vectors involves representing them with arrows (e.g., AB) to show direction, and the order of letters matters in the vector notation (AB ≠ BA).
• 😀 A position vector is one that originates from the origin (point O) and extends to a specific point in space, such as OA or OB.
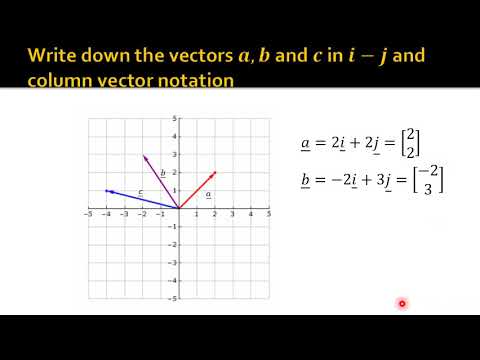
• 😀 Vectors can be expressed in different forms, such as column matrices, row matrices, or unit vectors. Unit vectors are commonly used in physics for vector representation.
• 😀 Non-position vectors are those that do not originate from the origin but from another point, and their expression involves subtracting position vectors to find the relative displacement.
• 😀 Vector addition and subtraction can be done by simply adding or subtracting the corresponding components (e.g., x and y components).
• 😀 To find the length (magnitude) of a vector, use the Pythagorean theorem, such as √(x² + y²) for 2D vectors.
• 😀 The length of a vector can also be written as its modulus (e.g., |OB| for vector OB), and is calculated using the square root of the sum of the squares of its components.
• 😀 In three dimensions, the length of a vector is calculated as √(x² + y² + z²), extending the concept from 2D to 3D vectors.
• 😀 The lesson encourages memorizing common Pythagorean triples (like 3-4-5, 5-12-13) to make calculating vector lengths faster and easier in some cases.

Q & A

What is a vector, and how is it defined?

A vector is a line segment that has both magnitude (length) and direction. It is used to represent quantities that involve both size and direction, such as force, velocity, and displacement.

What is the significance of direction in a vector?

The direction of a vector is crucial because it indicates the path or orientation of the quantity being represented. For example, in physics, acceleration and force are not only defined by how much but also by where they are acting.

How is a vector typically notated?

A vector is often notated with an arrow above the letter representing the vector (e.g., →AB) or written as a pair of coordinates, such as (x, y) for two-dimensional vectors.

What is the difference between a position vector and a non-position vector?

A position vector starts at the origin (point O) and points to a specific location in space. A non-position vector, on the other hand, has a starting point that is not at the origin and represents a displacement between two points.

What is the role of a Cartesian coordinate system in vector representation?

The Cartesian coordinate system provides a framework for expressing vectors in terms of x and y (for 2D vectors) or x, y, and z (for 3D vectors). Vectors are represented by their coordinates in this system, making it easier to perform calculations such as addition, subtraction, and finding magnitudes.

How do you subtract vectors using position vectors?

To subtract vectors, you can subtract their position vectors. For example, vector AB is calculated as the position vector for point B minus the position vector for point A (i.e., →AB = →OB - →OA).

What is the formula for finding the length of a vector?

The length of a vector, also known as its magnitude, can be found using the Pythagorean theorem. For a vector with coordinates (x, y), the length is calculated as √(x² + y²). In three dimensions, the formula becomes √(x² + y² + z²).

How is a vector expressed in unit vector form?

A vector can be expressed in unit vector form by breaking it into its components along the x and y axes (in 2D) or x, y, and z axes (in 3D). For example, a vector (x, y) can be written as x * i + y * j, where i and j are unit vectors in the x and y directions, respectively.

What is a position vector, and how is it represented?

A position vector is a vector that starts at the origin (point O) and ends at a specific point in space. It is often represented by the coordinates of the end point, such as OA = (x, y).

How do you find the magnitude of a vector in 3D space?

In 3D space, the magnitude of a vector with coordinates (x, y, z) is calculated using the formula √(x² + y² + z²). This method extends the Pythagorean theorem to three dimensions.